CF1929E Sasha and the Happy Tree Cutting
ATZdhjeb
·
·
题解
题目大意
给定一棵 n 个点的树,再给定树上的 k 条链,求最少标记多少条边,使得每一条给定链上均有至少一条边被标记。多测。
数据范围:
$2\le \sum n\le 10^5$。
$1\le \sum 2^k\le 2^{20}$。
### 简要分析
首先,数据范围明示状压。
一个比较显然的想法是预处理出每一条边能贡献哪些链,然后注意到答案的上界是 $O(k)$ 的,所以每轮找出能贡献新链最多的一条边选上,进行一个贪心。当然,这样是错的,hack 数据放在最后。
那么一个更正确的做法是考虑 DP,令 $f_S$ 代表标记集合 $S$ 中的链的最小代价,然后拿每一条边都去更新一下,也就是 $f_{S\cup s_{i}} \gets \min\{f_{S\cup s_{i}},f_{S}+1\}$,其中 $s_i$ 是第 $i$ 条边能贡献的链的集合。这样直接做是 $O(2^kn)$ 的。
考虑优化上述做法。直觉上我们知道,可能有一些边对应的 $s_i$ 是一样的,这样的边可以优化掉。进一步地,考虑这 $k$ 条链的端点所构成的虚树,我们知道虚树的每一条边一定对应原树的一条链(不一定是给出的),且这条链上的所有边的 $s_i$ 都是相同的。因为如果一条给定的链经过了这条链上的某一些边而不经过其它的,那么就意味着它从链的中间“拐弯离开”或“结束”了,而在这两种情况中都应该在虚树上新建一个点,将这些边在虚树上分为两条边。
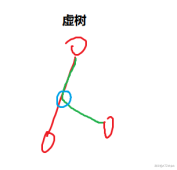
~~图是手画的,可能有点草率。~~
~~蓝点和最上面红点之间也有一段红边的,但是被覆盖了。~~
如上图,如果虚树上红边对应的 $s_i$ 不尽相同,那么必然有一条题目给定的链是如绿链那样的;但是在这种情况下,虚树中应该还有一个蓝点,这样那些 $s_i$ 不同的边就不会对应到虚树上的一条红边,而是一段红边和一段绿边。
我们知道虚树的大小是 $O(k)$ 的,因此虚树上的边数是 $O(k)$ 的,因此最多有 $O(k)$ 种互不相等的 $s_i$。我们只用这些不同的边去更新 DP 数组就可以了。时间复杂度 $O(2^kk)$,可以通过本题。
### 代码实现
注意写的时候并不用真的把虚树建出来,只需要对 $s_i$ 去重就可以了。
针对上文错误贪心的 hack 数据在代码最后的注释里。
```cpp
#include <bits/stdc++.h>
#define ll long long
#define mp make_pair
#define pii pair<int,int>
#define cpx complex<double>
#define INF 0x3f3f3f3f
#define mod 998244353
#define rep(i,a,b) for (int (i) = (a); (i) <= (b); ++(i))
#define per(i,a,b) for (int (i) = (a); (i) >= (b); --(i))
using namespace std;
inline int input() {
int x = 0,f = 1;
char c = getchar();
while (c < '0' || c > '9') {
if (c == '-') f = -1;
c = getchar();
}
while (c <= '9' && c >= '0') {
x = (x << 3) + (x << 1) + (c ^ 48);
c = getchar();
}
return x * f;
}
inline char get() {
char c = getchar();
while (isspace(c)) c = getchar();
return c;
}
const double PI = acos(-1);
int T,n,k,a[100010],dep[100010],fa[100010],dp[1000010];
vector<int> e[100010];
void DFS1(int u,int p) {
fa[u] = p;
dep[u] = dep[p] + 1;
for (int i : e[u]) if (i != p) DFS1(i,u);
}
void modify(int u,int v,int k) {
if (dep[u] < dep[v]) swap(u,v);
while (dep[u] != dep[v]) {
a[u] |= (1 << k);
u = fa[u];
}
if (u == v) return;
while (u != v) {
a[u] |= (1 << k);
a[v] |= (1 << k);
u = fa[u];
v = fa[v];
}
}
void solve() {
n = input();
rep (i,1,n) a[i] = 0;
rep (i,1,n) e[i] = vector<int>();
rep (i,1,n - 1) {
int u = input(),v = input();
e[u].push_back(v);
e[v].push_back(u);
}
DFS1(1,0);
k = input();
rep (i,1,k) {
int u = input(),v = input();
modify(u,v,i - 1);
}
rep (i,1,(1 << k) - 1) dp[i] = INF;
sort(a + 2,a + n + 1);
int N = unique(a + 2,a + n + 1) - a - 1;
rep (i,2,N) rep (j,0,(1 << k) - 1) dp[j | a[i]] = min(dp[j | a[i]],dp[j] + 1);
printf("%d\n",dp[(1 << k) - 1]);
}
int main() {
T = input();
while (T--) solve();
return 0;
}
/*
1
8
2 1
3 1
4 3
5 2
6 2
7 3
8 1
5
1 8
4 6
7 1
8 2
6 3
*/
```