【更新 NOIP 2025】顺着风的方向:CSP-S2 & NOIP 真题计划
JuRuoOIer
·
2025-10-29 22:13:38
·
算法·理论
顺着风的方向。
:::align{right}
——枫原万叶
:::
说明
浏览次数:
题解部分有些东西是去题解区抄的,不过每题保证至少有一个做法不是整篇抄的(即使它很可能和题解区某篇或几篇很像)。没有使用 GenAI。
根据 eteste 结果,本文当前共 24000 汉字,不含标点。
更新日志:
【本版,管理大大可以只看这些内容】30/12/2025:在参加 M***C*** 的过程中发现的问题:
修复了 CSP-S2 2021 T2 中不恰当的表述。
补全了 CSP-S2 2021 T4 中的知识点(统计部分是正确的,不影响)。
修正了 NOIP 2021 T2 中的知识点(统计部分是正确的,不影响)。
修正了 NOIP 2021 T3 中推式子部分不恰当的表述。
14/12/2025:复训并写完了山东省 NOIP 迷惑行为大赏。来补这里。
更新了 NOIP 2025 的个人题解。时间原因 T4 只写一种做法(虽说视频里也只简单提及了三种)。
更新了含有 2025 年赛事的考频统计和考点趋势折线图。
更新了一个考场上判断题目难度的技巧。
删除了由于写作时间跨度太大导致标准十分不统一的锐评难度。
注意到某个卷王已经过掉了历年 NOIP 几乎所有题,所以恢复之前删去的题目筛选及分类信息。
12/11/2025:提前发布了本文 NOIP 前的终版。如不出现较大锅 NOIP2025 前将不再更新。
更新了 CSP-S2 2019 和题解及涉及的好题推荐。
更新了押题部分的相关信息。
再次回复@快速数论变换 的建议:为了方便大家做题只管把两道出题人想考高精度但 __int128 可过题(2019 和 2020 各一道)标注一下吧。
回复忘了是谁了(ta 已经删评了)关于我个人对 CSP-S2 2025 难度评价的评论:私以为在这种地方难度还是有必要考虑一下客观现实。CSP-S2 2025 的难度横向对比往年 CSP-S2 确实处于中等,对比往年 NOIP(不过 NOIP 确实较难)确实较简单,且思维链上大部分的点(也在题解里说明了)都很大程度上有迹可循。不过作者的水平确实不高,本文的风格中也有一定体现(洛谷的高水平选手题解通常 习惯使用大量公式代替语言表达),所以作者远需努力。
借楼宣传今年的山东省 CSP-S2 迷惑行为大赏。
借楼预告今年的山东省 NOIP 迷惑行为大赏。
4/11/2025:
更新了春季测试 2023 的题解及涉及的好题推荐。
回复@快速数论变换 的建议:双下划线开头的内容 21 年起才允许使用,秉承尊重历史、尊重出题人的原则不做修改。
2/11/2025:进行如下更新(不分顺序)。
更新了 CSP-S2 2025 的题解及涉及的统计信息和好题推荐。
根据@ljw0102 的建议,更正了 CSP-S2 2022 B 的知识点。
根据@Tiffake 的建议,更正了 NOIP2024 D 中的 typo,并补上了算法和难度锐评。
根据@_O_vO 的建议,更正了 CSP-S2 中首次卡掉 \log 的时间。
更新了押题的部分,不过为了防止组题人看到相关内容,本文在考前最后一周会再更一版,为了防止届时审核审不出来可以预先收藏。我们在 S2 2025 中作出了确实有用的预言,所以玩原神对 OI 确有帮助。
借楼预告今年的山东省迷惑行为大赏已经换新链接了,在 12/11/2025 版更新内容里。
31/10/2025:最后三道题也更完了,至此 2020 到 2024 年除送分题和大模拟外的所有联赛题都可以在本文找到。
30/10/2025:更新了 NOIP 2024 的题解。
29/10/2025:更新了考频分布和推荐题单,并投稿洛谷全站推荐。
26/10/2025:完成了 CSP-S2 2024 和 NOIP 2023 二三题的文字题解。
19/10/2025:重整了这篇博客,删掉了所有的代码。不贴代码了,再贴我破机器打不开编辑界面了。
可能会 typo 或者脑抽犯错,如果您发现了任何问题(无论文字还是视频)欢迎通过 B 站、洛谷或者 QQ 撅我。
做这个东西的灵感主要来自枫原万叶的起飞语音“顺着风的方向”及各 whk 教辅的考频统计。这篇文章的主要目的:
把真题用像我这种彩笔能理解的方法讲一下,同时敦促我自己补题。
期望能从试题的变化趋势中发掘出额外的价值。不过只是个实验,还是先观望吧,毕竟每年出题人都不一样。
各板块考频及分布
按照板块分类统计,且除 入门组大纲内且不是题目核心考察内容的知识点 外没有其他可分入板块的知识点的(例如纯思维题),由于难以界定是否是思维题,一律归类为基础算法。板块之间不排序。
数据结构:11 次,共 9 题。
CSP-S2 2020 D(单调队列)
CSP-S2 2021 A(堆)
NOIP 2021 D(线段树,并查集)
CSP-S2 2022 B(多种高级数据结构选一)
NOIP 2022 D(线段树)
NOIP 2023 B(并查集)
NOIP 2023 D(线段树优化 DP)
NOIP 2024 D(线段树)
CSP-S2 2025 C(二维数点)
NOIP 2025 C(线段树优化 DP)
NOIP 2025 D(ST 表,单调队列)
数学:5 次,共 4.5 题。
NOIP 2020 D(拉格朗日插值)
NOIP 2021 A(筛法)
NOIP 2021 C(推式子)
NOIP 2022 A(加法原理,乘法原理)
NOIP 2024 B(加法原理,乘法原理)
动态规划:12 次,共 9.5 题。
CSP-S2 2021 B(区间 DP)
CSP-S2 2021 D(区间 DP)
NOIP 2021 B(数位 DP)
NOIP 2021 C(普通多维 DP,滚动数组)
CSP-S2 2022 D(树形 DP)
NOIP 2022 C(树形 DP)
NOIP 2023 D(线段树优化 DP)
CSP-S2 2024 C(普通多维 DP)
NOIP 2024 C(树形 DP)
CSP-S2 2025 D(普通多维 DP)
NOIP 2025 B(普通多维 DP)
NOIP 2025 C(线段树优化 DP,树形 DP)
图论:5 次,共 3.5 题。
CSP-S2 2020 C(拓扑排序)
NOIP 2020 A(拓扑排序)
CSP-S2 2021 D(最短路)
NOIP 2022 C(缩点)
CSP-S2 2025 B(最小生成树)
字符串:4 次,共 3.5 题。
NOIP 2020 B(扩展 KMP)
CSP-S2 2022 C(集合哈希)
CSP-S2 2023 B(进制哈希)
CSP-S2 2025 C(进制哈希,trie)
搜索:1 次,共 1 题。
CSP-S2 2022 A(Meet-in-the-middle)
基础算法:18 次,共 17 题。
CSP-S2 2020 A(模拟)
CSP-S2 2020 B(位运算)
CSP-S2 2020 D(贪心)
NOIP 2020 A(高精度)
NOIP 2020 C(分治)
CSP-S2 2021 C(贪心)
NOIP 2022 B(模拟)
CSP-S2 2023 A(枚举)
CSP-S2 2023 C(模拟)
CSP-S2 2023 D(二分,贪心)
NOIP 2023 A(贪心)
NOIP 2023 C(贪心)
CSP-S2 2024 A(贪心)
CSP-S2 2024 B(二分,贪心)
CSP-S2 2024 D(若干基础算法)
NOIP 2024 A(贪心)
CSP-S2 2025 A(贪心)
NOIP 2025 A(贪心)
得到统计图:
NOIP 2025 与我们所猜的“大概率情况”基本是拟合的,不过一个是难度有点离谱;一个是线段树靠前放到了树形 DP 题上,DS 题最终考的单调队列和 ST 表。
T4 部分题解有点标题党,单调数据结构不是普及的。虽然感觉普及的基本上也会吧
发现:
右图中总数不断减小可以看出思维越来越重要。
左图中配合表显而易见的是 21 年开始 DP 和线段树年年都在考 ,而贡献了基础算法绝大部分题的贪心 同样十分重要。
另外似乎有一个挺重要的点在于发现 题目中不同寻常的限制,进而发掘 解题所需的关键性质。
我赌明年还考串串。谁赞成,谁反对?
:::info[NOIP 2025 前版]
在 CSP-S2 2025 前,我们猜中了:
会考图论算法 。会考贪心。(这不也是废话吗怎么可能不考)会考 DP。(这不是废话吗怎么可能不考)
发现:
右图中总数不断减小可以看出思维越来越重要。
左图中配合表显而易见的是 21 年开始 DP 和线段树年年都在考 ,而贡献了基础算法绝大部分题的贪心 同样十分重要。
其实根据数据和 CSP-S2 题目知识点的分布 NOIP 正常来说算法向题目 (思维向很难猜吧??!)该考什么已经有个差不多了,我也看不出朵花来。实在想知道我猜测结果的等考前一周上 B 栈找吧。
::::info[CSP-S2 2025 前版]
发现:
无知识点及 DP 的比重加大可以看出思维越来越重要。
左图中配合表显而易见的是 21 年开始 DP 和线段树年年都在考 ,而贡献了基础算法绝大部分题的贪心 同样十分重要。
另外就是图论算法好像两年没碰过了,今年……算了不说了自己悟吧。
::::
另外,根据上表,外加做题的实际感受,笔者也挑出了若干值得一做的题并按算法将它们进行了分类。如果你有未完成的难度适合自己的题(比如目标是 NOIP 200+ 的就可以考虑做全部题了,而目标是正常省份一等的可以先锚定蓝和较容易的紫),建议在联赛之前最起码看一遍,做到充分理解。其中加粗表示十分推荐,不加粗表示比较推荐,星号表示超纲,斜体表示比较难,算法之间仍然不排序。
推荐题:
CSP-S2 2019 D1C CSP-S2 2019 D2A CSP-S2 2019 D2B CSP-S2 2019 D2C CSP-S2 2020 C CSP-S2 2020 D
NOIP 2020 C *NOIP 2020 D
CSP-S2 2021 A
CSP-S2 2021 B CSP-S2 2021 D NOIP 2021 B NOIP 2021 C NOIP 2021 D
CSP-S2 2022 A
CSP-S2 2022 B CSP-S2 2022 C CSP-S2 2022 D NOIP 2022 B NOIP 2022 C NOIP 2022 D 春季测试 2023 C
春季测试 2023 D CSP-S2 2023 B
CSP-S2 2023 D
NOIP 2023 B
NOIP 2023 C
NOIP 2023 D CSP-S2 2024 D NOIP 2024 A
NOIP 2024 C NOIP 2024 D CSP-S2 2025 B CSP-S2 2025 C CSP-S2 2025 D NOIP 2025 B
NOIP 2025 C NOIP 2025 D
:::info[剧透版]
数据结构
CSP-S2 2020 D
CSP-S2 2021 A
NOIP 2023 B
NOIP 2021 D
CSP-S2 2022 B NOIP 2022 D 春季测试 2023 D NOIP 2024 D CSP-S2 2025 C NOIP 2025 D
数学
动态规划
CSP-S2 2019 D2A *CSP-S2 2019 D2B
CSP-S2 2021 B NOIP 2021 B NOIP 2021 C CSP-S2 2022 D NOIP 2022 C 春季测试 2023 C
NOIP 2023 D NOIP 2024 C CSP-S2 2025 D NOIP 2025 B
NOIP 2025 C
图论
CSP-S2 2020 C CSP-S2 2021 D CSP-S2 2025 B
字符串
CSP-S2 2022 C CSP-S2 2023 B
CSP-S2 2025 C
搜索
思维、Ad-hoc
CSP-S2 2019 D1C CSP-S2 2019 D2C NOIP 2020 C *NOIP 2020 D
NOIP 2022 B CSP-S2 2023 D
NOIP 2023 C
CSP-S2 2024 D NOIP 2024 A
:::
考场小寄巧
:::warning[阅读前须知]
下面这些东西全部根据本文的统计写出,只针对大概率情况。没有任何明文要求对题目的难度与部分分间的关系加以限制。作者不对相信下面内容导致的后果负任何责任。
而且你别忘了,这段话出题人也是能看见的哟 \~
:::
在 NOIP 2025 中,我校一位去年获得 Ag 的神犇今年只有(这对 Ag 爷来说真不高吧?)200 分。据教练说,原因是其 T2 做了比预期长的时间然后崩溃了。
所以我们合理反推一下:这位神犇根据往年的经验天真地以为 T2 是蓝,然后没有一眼秒掉,然后调样例可能还调了很久,然后就崩溃了。
如何避免出现这种情况呢?
这里根据往年题的情况,给出一个在联赛中 判断出题人所设计的难度的技巧。再次提醒,这只是个参考,准度不是 100\% ,所以主要用于给自己找自信,考场上不要因此使心态变差 。
如果此题的设计难度为送分题 或基础题 (洛谷蓝或以下 ),他通常会给出至少 40 分的无脑分。
例如 NOIP 2024 T1 的暴力、A 性质、B 性质共计 60 分全是无脑分,CSP-S2 2025 T2 默写 Kruskal 板子有 48 分,套层暴力枚举有 80 分(卡时或者精细实现其实是可过的)。
如果此题的设计难度为有一定难度的题 (洛谷接近紫的蓝 或紫 ),他通常只会给出不超过 40 分与正解无关的(但可能需要一点点脑子)部分分,而且通常需要拼至少三四个包。
例如 NOIP 2024 T3 的 k=1 、链性质和菊花性质共有 40 分,NOIP 2025 T2 的暴力和 A 性质共有 28 分(B 性质就与正解有关了)。
如果此题的设计难度为防 AK (洛谷上位紫 或黑 ,不过也有简单场),他通常最多只会给出两三个点的暴力分,能状压的题给再最多两三个点的状压分(少则根本没有),而且鲜有与正解无关的性质。
例如 CSP-S2 2023 T4 即使是蓝题也没有暴力分、只有少量状压分,NOIP 2024 T4 没有不用数据结构能做的分,NOIP 2025 T3 只有 8 分的爆搜分,T4 没有暴力分。
文字题解
已更完从有 CSP-J/S 以来除 CSP-S2 2019 JX 外所有 CSP-S2 和 NOIP 题目的题解。
CSP-S2 2019
第一次 CSP-S,难度十分神人。
送分题不讲。
D1B - P5658 [CSP-S2019] 括号树
括号匹配题,求的还是子串个数,和 S2 2023 消消乐颇像。
设现在有 cnt 层左括号未匹配,沿用消消乐的思路我们可以在遍历整棵树的过程中对每个 0\le i\le n 维护出 cnt=i 的情况数,然后就做完了。
但是有点问题,这个题是分左右括号的,消消乐没区分。所以当 cnt<k 时,cnt=k 的情况数应该清零,所以维护的时候改用栈。栈底要保持有一个元素记录 cnt=0 即当前已经完全匹配的情况。
然后空间不允许栈开在函数里,所以把栈开在全局,回溯的时候一定要考虑好下一个位置到底对栈做了什么修改。
下一个是左括号:只会向栈中插入 0 ,所以删除栈顶即可恢复。
下一个是右括号:分大小是否为 1 考虑。
栈大小为 1 时:只会导致栈底值清零,向下递归前记录栈底值然后替换回来即可。
栈大小超过 1 时:会导致顶层被删除且下一层被减一,记录最上面两层的值即可。
复杂度 O(n) 。
D1C - P5659 [CSP-S 2019] 树上的数
对脑电波大获全胜,思考时长不到 1.5 小时。
由于要的是最小的字典序,肯定先保小的数字。对于一个数字,贪心地找到其能到达的最小的点即可。
但是路径之间可能会冲突,所以要确保数字能真的到达目标点,就要求:
起始边必须是起点删掉的第一条边,确保要移动的数字在起点上;
每个途径点删掉的两条边删除顺序必须连续,确保要移动的数字按照希望的路径走;
结束边必须是终点删掉的最后一条边,确保数字移动过去之后不要再被移走。
所以我们需要为各个边安排合理的删除顺序以确保每个路径正常移动。根据刚才的要求,
起始边要放到起始点删边顺序的最前面;
途经点需要插入连续两条边;
结束边要放到终点删边顺序的最后面。
插入操作不难用链表维护。对每个数字初始所在的点为根扫整棵树,判断每个点能否作为途经点及能否作为终点即可。复杂度 O(n^2) 。
根据题解区,也可以不用链表而是对于每个点建图,把原图的边建成新图的点,然后可以用并查集维护相关信息,这样更加直观。复杂度根据并查集优化程度 O(n^2\alpha(n)) 到 O(n^2\log n) 不等。
D2A - P5664 [CSP-S 2019] Emiya 家今天的饭
典得没边了。感觉 99.9\% 的人做过,我是那 0.1\% 。
首先的首先,计数题七字真言,爆搜、DP、推式子。
首先在 CSP-S2 2025 的毒打后我们看到一个东西限制选一半就知道至多爆一个。
不难想到枚举爆掉的食材,此时设 dp_{i,j,k} 表示前 i 个烹饪方式中总共选了 j 次食材,我们枚举的那个(设为 x )被选了 k 次。这样不 贡献答案的状态就是 k>\lfloor\frac{j}{2}\rfloor 的情况。转移直接从上一列分类讨论一下就行:
不选:dp_{i-1,j,k}\to dp_{i,j,k} ;
选但没选到 x :dp_{i-1,j-1,k}\cdot\left({\displaystyle\sum_{l\in[1,m],l\neq x}a_{i,l}}\right)\to dp_{i,j,k} ;
选到 x :dp_{i-1,j-1,k-1}\cdot a_{i,x}\to dp_{i,j,k} 。
每种烹饪方式的和显然可以预处理。
至于为什么上述过程只能求不符合要求的情况,因为我们只能确定 x 是否爆了,没管其他的是否爆了。
所以还得拿总数减。当然这个对连刚才的过程都能理解的你来说就很容易了,设 g_{i,j} 表示前 i 种烹饪方法做了 j 个菜的方案数,讨论当前这个方法做没做菜即可。
然后我们获得了一个复杂度 O(mn^3) 的优秀算法,可惜过不去。
如果你顺着读我的题解你会发现前面那玩意就很有病:是怎么能做到直接发现设计 dp 数组是用来求不符合条件的情况的?
当然原因我也解释了:在方程推完之后我们知道它没法正向求。
那既然不能正向求,有没有什么更加省事的方法呢?
有的,兄弟,有的。
我们只在乎 k 与 \lfloor\frac{j}{2}\rfloor 的关系,而不在乎它们的具体数值。
然后有无数种办法搞个式子把后两维状态合并成一个能表示上述两者关系的状态。比如 2k-j 。于是如果我选到 x 上这一维就加 1 否则就减 1 。转移方程和上面本质其实是一样的:
dp_{i,j}=dp_{i-1,j}+dp_{i-1,j-1}\cdot\left({\displaystyle\sum_{l\in[1,m],l\neq x}a_{i,l}}\right)+dp_{i-1,j+1}\cdot a_{i,x}
然后复杂度就降到 O(mn^2) 了。
D2B - P5665 [CSP-S 2019] 划分
考虑暴力 DP,设 dp_{i,j} 表示枚举到 i 最后一次断掉了 j 的答案。暴力转移枚举 j 的上一个断点,复杂度 O(n^3) 。
观察枚举的过程,发现在 j 变大时 k 能取的范围的右端点显然会往右。于是用单调队列维护可以实现复用信息,复杂度 O(n^2) 。
类似于后文中某题(由于编写顺序原因这场是最后加上去的所以前文引用后文),DP 优化不动时有必要考虑贪心。
由于本题中 a_i\ge 1 ,所以有 (a_i+a_j)^2=a_i^2+a_j^2+2a_ia_j>a_i^2+a_j^2 ,即能不合并就别合并。所以最后一段应该尽可能小一点,而由于终点固定,其实就是让这段区间短一点。
于是根据刚才得出的 k 的右端点的单调性我们不再枚举 j ,只枚举 i 并找到最大的合法的 j ,这仍然可以单调队列。
手写高精度的话有些卡常可以试着压位(两个 long long 就搞定了),不过我们是现代人,他总的答案不超过 (n\sum a_i)^2\le 1.6\times10^{33} ,根据公式 2^{10}\approx10^3 估算知道可以 __int128。
复杂度线性。
D2C - P5666 [CSP-S 2019] 树的重心
采用@xht 大佬的做法,简单解释了一下式子,方便和我一样不熟悉树的重心的选手理解。
首先将原式视为统计各点做重心次数的和。
根据 OI-Wiki,树的重心具有如下性质:
树的重心如果不唯一,则恰有两个。这两个重心相邻。而且,删去它们的连边后,树将变为两个大小相同的连通分量。
在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
把两棵树通过一条边相连得到一棵新的树,那么新树的重心在连接原来两棵树的重心的路径上。
一棵有根树的重心一定在根结点所在的重链上。一棵树的重心一定是该树根结点重子结点对应子树的重心的祖先。
因为树上两点间路径唯一,删掉一条边后形成的两棵子树间路径必然经过这条边,根据上述第三条,我们取树的一个重心为根,则首先除根外一个点做重心时删掉的边必然不是其子树内的边 。
设 sz_i 表示 i 的子树大小,并预处理出每个点的重儿子 son_i 。若删掉边 (k,fa_k) ,此时根据重心的定义 k 内 x 外的部分及 x 的重儿子均不能超过 \lfloor\frac{sz_k}{2}\rfloor ,即 2(sz_k-sz_x)\le sz_k 且 2sz_{son_x}\le sz_k ,去括号并移项得 2sz_{son_x}\le sz_k\le 2sz_x 。
所以我们需要求出不在 x 子树内(不含 x )的满足上述式子的 k 的数量。式子就是个单点加区间求和,随便搞个 ds 维护一下,跑两遍 dfs 即可。子树内点数这块,在第一遍 dfs(往 ds 上挂点信息)时,进子树的时候查询一遍式子,出子树的时候再查询一遍式子,减一下就是子树内符合条件的点数。
然后考虑根节点做重心的问题。这个时候可能把 son_{rt} 里的边割掉了,此时由糖水不等式(\frac{a}{b}<\frac{a+c}{b+c}(0\le a<b,0<c) )有 \dfrac{sz_{son_{rt}}-a}{sz_{rt}-a}<\dfrac{sz_{son_{rt}}}{sz_{rt}} ,所以 son_{rt} 必然合法,所以只需要看根节点次大的儿子是否合法即可;割掉其他边时则还是看最大的儿子是否合法。dfs 时顺便维护即可。
复杂度 O(n\log n) 。
CSP-S2 2020
题目难度不大,写完难度巨大。好在大样例蛮强的,要不然至少考场上我儒略日是肯定要 0pts 了。
A - P7075 [CSP-S2020] 儒略日
由于数据范围很大,所以我们要尽可能地划分周期以加速。下面列出一年以上的周期。
对于儒略历:只有 4 年周期,一周期 365\times4+1=1461 天。
对于格里高利历:需要 400 年、100 年和 4 年三种周期,分别为 146097 天、36524 天和 1461 天。
这样一周期不超过一年,可以直接模拟。
注意除最大的周期可以直接取模外,其他周期的出现次数不能大于或者等于更大的周期的年数除以该周期年数的商(例如 100 年周期最多只计算 400\div 100-1=3 次)。
B - P7076 [CSP-S2020] 动物园
显然如果知道了需要购买的饲料能养的编号最大的动物的编号中有 k 个 1 ,则能养的动物种类总数是 2^k ,然后减掉已经养了的即可。
购买饲料时显然按照所有动物的或和购买,记录购买的集合后对于每一个二进制位枚举其是否需要饲料即可,不需要饲料的位同样或入或和中。
记得开 __int128。
C - P7077 [CSP-S2020] 函数调用
被蓝题击毙了。
操作类题目的思路基本上是固定的:先不考虑其中一部分操作看能不能做,再加上被忽略的部分。
然后我们发现:
没有一操作显然直接处理出每个操作乘多少即可。
没有二操作,此时由于一操作不能像二操作一样合并进行,所以不能沿用没有一操作的方法;但是我们发现一操作之间的顺序是任意的,所以我们可以计算每个一操作调用了多少次。由于函数调用不会递归,即调用过程自身形成一个 DAG,这个过程是可以直接拓扑排序后遍历解决的。
没有三操作,此时对于一个一操作,我们可以求出其之前进行的二操作乘的总数 k ,然后将该操作的数字除以 k 加到原始数据上,这样可以将一操作和二操作分离处理。
因为没有一操作后三操作变得没有意义而导致难以增强为原问题,所以我们忽略这种情况,只考虑后两者。遂发现后两者是可以合并的:在没有二操作时,我们可以计算每个一操作调用了多少次,而考虑进二操作之后我们参考没有三操作的做法,可以知道每个函数在调用之前一共乘的数 k ,从而知道涉及每个一操作应该计算 k^{-1} 次,然后就做完了。
但是,上述思路只是思考过程中比较自然的想法,劝大家写的时候按函数执行的顺序倒着跑,即加法操作的次数不按上一句说的使用调用之前乘的数的逆元、计算答案时先加后乘,而是使用调用之后乘的数、计算答案时先乘后加,否则处理乘 0 相当麻烦。别问我怎么知道的,问就是我写了一遍正着跑的然后发现可能乘 0 ……
D - P7078 [CSP-S2020] 贪吃蛇
这题是有里程碑意义的:因为它标志着 CCF 能卡 \log 了。
虽说是黑题,但是本身想到做法的难度不大(虽然主要是靠猜但是并不难猜,我找了两个分别退役两年半、三年的 whk 选手都猜出来了 ww),重点在如何落实边界情况,这在 OI 赛制的考场上同样是有区分度的,要是是我很可能就被区分了。
首先对着小样例开始猜,随便猜几个(比如我是第二次猜到的)发现猜到“当大的吃小的后不会变为最小的就吃”的时候发现能过样例,于是大胆假设它是对的并试图证明。然后我们发现证明是容易的:
假设所有的蛇从小到大是 a_1,a_2,\dots,a_n 。
最大的吃完最小的后不会变成最小的,即 a_n-a_1\ge a_2 ,此时如果 2 被 n-1 吃(若还是被 n 吃且吃完后 n 不是最小的则可以将前两个视为一个,所以不需要额外考虑),则由于 a_{n-1}\le a_n 而 a_1\le a_2 根据不等式的同向可加性有 a_{n-1}-a{2}\le a_n-a_1 ,故 n 将在下次吃之前永远不会变为最小的。
但这并不是能吃的唯一情况。我们刚才显然是没有考虑“吃了之后会变成最小的”的情况的。这种情况一定不能吃吗?
答案是否定的。我们考虑如果吃了之后会变成最小的,则下一条蛇有两种可能:
如果吃了不会变成最小的,或者只剩两条蛇,此时根据刚才“当大的吃小的后不会变为最小的就吃”的结论可以放心吃,此时当前的蛇则因此不敢再吃了。
否则,问题递归下去,由于上一种情况中有“只剩两条蛇”的条件,所以递归一定有终点。此时当前蛇根据终点与当前蛇之间的蛇数量的奇偶性来决定是否吃:如果是奇数则可以,因为下一条蛇不敢再吃一次;如果是偶数则不行,因为下一条蛇可以吃。
直接用 set 之类的东西存一下可以做到一个 \log ,理论上只有 70 分。
但是题中为我们排好序了,所以我们可以直接维护一个双端队列用来存蛇,根据刚才证明“当大的吃小的后不会变为最小的就吃”性质的过程,每次吃完后的蛇的大小是单调递减的,故我们可以再维护一个双端队列用来存吃之后的蛇,每次从两个队列尾部取最大值,头部取最小值,然后到最后一次单独扫一遍判断一下即可实现 O(n) 。
NOIP 2020
A - P7113 [NOIP2020] 排水系统
题目中保证图为一 DAG,然后该题即为拓扑排序板子,这里不再赘述。
本题需要高精度,作者懒得写了所以不附代码。
B - P7114 [NOIP2020] 字符串匹配
设原串为 s ,下标从 0 开始。
先考虑一个弱化版的问题:如果不考虑 A 中出现奇数次的字符数比 C 中出现奇数次的字符数少这个条件,我们该如何求解。
这个东西是容易的,我们先将字符串各位置的 z 函数求出来,然后枚举循环节长度。
我们发现,枚举的循环节长度为 i 时,原式中 AB 的循环次数 k 有 \left\lfloor\dfrac{z_i}{i}\right\rfloor+1 个取值,因为 s[0,z_i-1]=s[i,i+z_i-1]\Rightarrow s[0,i-1]=s[i,2i-1]=\dots=s\left[\left\lfloor\dfrac{z_i}{i}\right\rfloor\cdot i,\left(\left\lfloor\dfrac{z_i}{i}\right\rfloor+1\right)\cdot i-1\right] ,如果不懂上面的证明可以自行画图理解(或者直接去看第一篇题解的图)。
然后我们考虑刚才忽略的限制。这里我们仍设字符串 AB 的循环次数为 k 。根据限制内容,不难想到下述 k 是偶数的部分,遂按照 k 的奇偶性讨论:
对于 k 是偶数的情况,所有 AB 中涉及到的字符均在 (AB)^k 中出现了偶数次,这对 C 中各字符的奇偶性显然是没有影响的,所以定义域内无论 k 取何值 C 中出现奇数次的字符数量和 f(s) 相等;
对于 k 是奇数的情况,类比偶数的情况,因为奇数可以表示为 2n+1 的形式,所以定义域内无论 k 取何值 C 中出现奇数次的字符数量和 f(s[i,n-1]) 相等。
所以我们需要求出(此处 f 与题目中 F 同义):
对于每个 0\le i\le n-1 ,求出 f(s[i,n-1]) ,这个直接开桶倒着扫一遍即可;
对于每个 1\le i\le n-1 ,求出 f(s[0,0]),f(s[0,1]),\dots,f([0,i-1]) 中大于 f(s[i,n-1]) 的和大于 f(s[0,n-1]) 的数的个数分别是多少,首先 f(s[0,0]),f(s[0,1]),\dots,f([0,i-1]) 可以扫一遍求出来,然后扫的过程中用一个数据结构(比如树状数组或者线段树)或一个容器(比如 std::set)存一下(或者由于其值域只有 26 可以考虑开桶做到 26 甚至把桶开到树状数组或者线段树上做到 \log 26 ),就可以按上述方法求解答案了。
这样我们就做完了,根据实现方式不同复杂度为 O(n\log n) 、O(26n) 或者 O(n\log 26) 不等。
C - P7115 [NOIP2020] 移球游戏
看到本题容易联想到 hanoi 塔,于是不难想到考虑最小的也就是 n=2 的情况。
此时我们先将其中一列排序:
记该列中颜色 1 的个数为 k 。
先将另一列顶部的 k 个球移入空列。
然后将该列中颜色 1 的球移入另一列中,颜色 2 的球移入空列中。
然后先将移入空列中的球放回,再将移入另一列中的球放回,这样这一列就实现了上面全是颜色 1 而下面全是颜色 2 。
在这之后,我们将另一列中移入空列的球放回,将该列中颜色 1 的球放入空列,然后将另一列中的球归类,我们就用 2m+3k 次操作完成了 n=2 的问题。这里,由于到底谁是颜色 1 并不妨碍做题,k 最大为 \left\lfloor\dfrac{m}{2}\right\rfloor ,故总操作次数最多为 \dfrac{7m}{2} 次。
此时顺着 hanoi 塔的思路,我们需要将 n 更大时的问题转化为 n=2 的问题。遂考虑 n=3 的情况。
我们发现,n=3 其实是没法直接像刚才 n=2 那样做的,所以我们转化为 n=2 就只能分出一种颜色。怎么分呢?
既然我们会做 n=2 ,那我们将不需要分出的颜色视为一种,而需要分出的视为另一种,这样我们就可以跑 n=2 的算法了。想到这一步,这题其实就做完了:每次将处理的颜色区间 [l,r] 分为 [l,mid] 和 [mid+1,r] 然后两两跑 n=2 的分类。总操作次数 \dfrac{7nm}{2}\lceil\log n\rceil 次完全可过。
D - P7116 [NOIP2020] 微信步数
个人感觉出得极好的一题。也纪念我第二次独立完成紫题。
这是一篇多图长文,希望能对大家有所帮助。
第一步:快速求一个点的答案
为了方便画图,我们先假设 k=2 ,即问题在平面内。
假设我们的路线是这样的:
那么一个显然的想法是直接走红色的路径:
但是这立刻出现一个显然的问题:如果开始位置比较靠边,可能没有办法走完全部 n 步就出界了。所以我们需要先判断当前起始的位置是否会出界,如果不会就走红色的路线直到到达一个会出界的起点,然后暴力地走 n 步。
上述过程中显然只有走红色路线的部分有较大优化的空间:我们希望一下子算出走多少步之后会到达一个会出界的起点。
于是我们需要知道在靠边缘多近时我们才会出界。这意味着我们需要求出路线的四至点。下图中假设起点位于 (0,0) ,采用传统坐标系。
路线中向上、下、左、右最多分别会走一格、两格、一格、两格,也就是说,上、下、左、右最靠边的分别 1 、2 、1 、2 格范围内的所有点作为起点时会在 n 步内出界。由于最终的合位移最多只会向两个方向,因此直接判断哪个方向更先到达上述范围,然后算出到达上述范围的步数即可。
第二步:快速求每个点的答案
我们这里以一个 8\times8 的格为例。
即使都是作起点时 n 步内会出界的点,出界所需的步数也是不一样的。接续刚才求“四至点”的思想,其实我们完全可以对每一步都求四至点,这样就知道最靠四边的每一行(或者列)会在多少步内移出了。比如:
是上述路线中所有会改变路线四至点的步数。这启发我们不需要维护每一步的四至点,而在四至点变化的每一步维护上述 “最靠四边的每一行(或者列)会在多少步内移出 ”。由于这最多影响 n 行(或者列),所以我们可以开四个长度为 n 的数组分别存四边向内各行(列)出界所需的步数(显然只存一轮内能离开的行或列)。比如上述情况可存储为:
下标
1 2 3 4 \dots -3 -2 -1 0
\mathbf{x} 2 \dots 8 6
\mathbf{y} 1 11 \dots 4
而将上述数据放到地图里的时候,我们发现一个点可能存在于多个一轮内会出界的行(或者列)中,此时显然需要对所有的出界步数取最小值 ,因为这些步数中任何一个都会导致出界,而第一次出界之后就停止了。于是地图可以写成下面这样(数字表示右下角格点出界所需步数):
其中加粗的数字表示该格被多行(列)覆盖,取最小值。
边上的格子处理完了,接下来要处理内部的格子。
显然,如果路线有相对位移的话,走若干轮后一定会走到一个上图中有数字的位置,于是我们把格子填满:
其中黄底、绿底、蓝底格子分别需要额外走 1,2,3 轮。结合第一步中的快速移动至边上,中间部分的格子我们也就算出来了,于是我们已经完成了第二步:快速求出每个点的答案。
第三步:快速求所有点答案和
但是我们需要求所有点的答案之和。
刚才的图其实已经启发我们了:我们可以将格子的底色和数字分别求和。我们一个一个来考虑。
对于底色,我们发现同样颜色的块都是异形的,难以分开计算。但是我们发现一段颜色的后缀(最左上角的若干种颜色)拼起来是矩形,所以我们其实可以将 3b+2g+y 视为 b+(b+g)+(b+g+y) ,其中 b,g,y 分别表示蓝、绿、黄色区域的面积,这样我们就可以将底色表示的答案变成若干矩形的面积和了。如果一轮中 n 步合位移是 (x,y) ,则每个颜色后缀矩形依次增加 |y| 行、|x| 列 ,显然每个矩形的面积都是一个与颜色数相关的二次多项式,即若设有底色的所有格子构成大小为 a 行 b 列的矩形,则我们需要求的是 \displaystyle\sum_{k=0}^{\min\left\{\left\lfloor\frac{a}{|y|}\right\rfloor,\left\lfloor\frac{b}{|x|}\right\rfloor\right\}}(a-k|y|)(b-k|x|) ,其中求和符号内部的东西是一个关于 k 的二次多项式,且除 k 外的所有东西都是确定的,于是我们可以对所有的次数 i 求出 k^i 的总和并乘上这一次项的系数。
对于数字,我们发现如果一轮中 n 步合位移是 (x,y) ,则每种底色的格子只涉及 |y| 行、|x| 列,且每换一种颜色每行宽度减少 |x| ,每列高度减少 |y| ,这些都可以通过把上图画一遍来理解。于是这里变成了一个等差数列求和。
加上白底部分的答案(这显然在求解表格中值的时候就可以顺便求出来了),至此,我们已经解决了 k=2 的问题。
第四步:将做法扩展到更高维
其实其他维度的问题和 k=2 是相似的,只是最终的式子有所不同:底色部分变为一 k 次式子,数字部分变为一 k-1 次式子。而 \displaystyle\sum_{i=0}^n i^k 是一个 k+1 次多项式(证明可以参考此题题解区,不过本题暴力插值就行),故我们可以通过拉格朗日插值求出通项公式,然后就可以用上述方法解决了。至此,我们就完成了这道题目,复杂度 O(nk^2) 。
CSP-S2 2021
A - P7913 [CSP-S 2021] 廊桥分配
知识点:模拟、堆(或者类似的能维护最值的东西)、前缀和。
不考虑廊桥数量的限制,每个飞机都安排在尽可能靠前的廊桥时,每个飞机安排到的廊桥位置就是其能使用廊桥时所需最小的廊桥数量。这容易用两个堆分别维护空闲廊桥和占用廊桥的方式计算,其中维护空闲廊桥的堆按编号建立小根堆,维护占用廊桥的堆按离开时间建立小根堆,每次先处理所有需要解除占用的廊桥,再取出编号最小的空闲廊桥停机。算完这个后分别前缀和即可求出国内和国际区安排 i 个廊桥时可停靠航班数,然后扫一遍对 s1_i+s2_{n-i} 求个最大值即可。
记得把前缀和跑到 n ,只跑到 m_1,m_2 会 WA on #9,因为可能存在 m_1+m_2<n 的情况。
B - P7914 [CSP-S 2021] 括号序列
一个容易想到的思路是设 dp_{i,j,k} 表示考虑了前 i 个字符、有 j 个左括号还未匹配、前 i 个字符中最后有 k 个 * 的方案数,转移直接分别考虑这个位置能否填入 (、)、* 并按照上述状态定义转移即可。
但是这个做法是有问题的:形如 (SAS)(即 (*...*(...)*...*),两侧 * 个数不超过 k 个)的情况并不合法,而上述算法统计了这样的情况。
这种情况下,我们根据字符串变换的方式,可以考虑区间 DP:设 dp_{l,r} 表示符合条件的超级括号序列数量,则枚举断点 i 后分别考虑每种变换方式:
()、(S) 型:直接枚举 |S| 。(A)、(AS)、(SA) 型:枚举断点即可。AB、ASB 型:枚举断点,用前缀和优化一下枚举 |S| 的过程即可。
但这样第三类会每个断点都算一次导致很多重复。考虑去除重复。
考虑使每个第三类的合法串只在第一处断点被计算。这意味着,我们不再允许 DP 过程中将两个第三类连成一个大的第三类。
这是容易的:前两种情况的共同特征是最外面要套一层括号。所以我们按字符串最外面是否是相匹配的一对括号分类计算,上述错误做法中第三种情况则只允许断点左侧选择最外面是相匹配括号的情况。
C - P7915 [CSP-S 2021] 回文
:::warning[观看视频题解时请注意]
本题视频中的表述有点问题。文字题解是正确的,看视频题解时可以无视其与本题解的差异或者看置顶评论的勘误 。在此因给大家带来的不便谢罪。
:::
注意到由于每个数只会出现恰好两次,所以前一半和后一半必然是对称的两个排列 ,而由于每次往 b 里放的时候只会往后放所以后一半在 a 中是连续的,也就是要求 a 中有一个连续段是排列。不过这是有解的必要不充分条件所以我们没法用这个来判掉所有的无解。
但是我们其实没必要额外判断是否有解。直接每次贪心地取左侧的值,既然后一半是连续的那我取的这个值也必须和我之前取值对应的后一半是相连的,如果不是就不能取,反之一定能取。于是不确定的只剩下第一次取哪里,这个直接第一次先取左边跑一遍没跑出来再跑右边即可。
D - P7916 [CSP-S 2021] 交通规划
狼抓兔子加强版。
k=2 引用 xht 在 P4001 下的题解,其中给出了本题的关键性质:
平面图
边与边只在顶点相交的图。
对偶图
对于一个平面图,都有其对应的对偶图。
平面图被划分出的每一个区域当作对偶图的一个点;
平面图中的每一条边两边的区域对应的点用边相连,特别地,若两边为同一区域则加一条回边(自环)。
这样构成的图即为原平面图的对偶图。
定理
平面图最小割 = 对偶图最短路。
而在 k=2 且两点颜色不同(相同答案显然为 0 )时最优的方案明显是形如下图的(以样例为例):
也就是图中分为两个连通分量(定义有边相连的同色点为连通):询问给出的黑点连接若干染色得到的黑点形成一个连通分量,白色点同理。这其实就是这个图的最小割。
根据“平面图最小割 = 对偶图最短路”的定理,我们考虑先把对偶图建出来:
然后我们需要找到起点和终点。我们割掉的是两个连通块之间的边,所以边上一圈的点被两个给定点分成两部分,一部分连接起点,一部分连接终点,这样就能确保求出的最短路是能把原图割开的。
这样我们就把 k=2 的情况做完了。
完整做法
推广 k=2 的情况,大胆猜想一段连续的点同色点对应一个连通块。所以对偶图的各个起点应该在异色的给定点之间:
此时把原图割开就需要对起点进行配对后两两取最短路,这个过程可以无脑区间 DP 做到 k^3 ,然后只需要以每个点为起点跑遍最短路就做完了。
另外路线有时会转出去再转回来,所以同色给定点间也需要建点,只不过不进行配对。
:::info[相似题目推荐]
P4001 [ICPC-Beijing 2006] 狼抓兔子
:::
NOIP 2021
整场平均难度(按洛谷标出的):上位蓝。
A - P7960 [NOIP2021] 报数
注意到本题的值域并不大,直接预处理所有 1.1\times10^7 内的含 7 的数字的倍数,并用类似链表的结构,预处理出每个合法数字的下一个合法数字加速查询即可。
B - P7961 [NOIP2021] 数列
为了避免混淆,本题解中使用 K 表示题中的 k 。
计数题三个思考方向:爆搜、DP、推式子。
:::align{right}
——[Anonymely](),NOI2024 D 银,WC2025 金
仍然面向数据范围编程,数据范围很小但分析爆搜复杂度后发现差得远遂考虑 DP。
很难不注意到这玩意是需要处理进位的,遂从低往高考虑,不难设计出状态 dp_{i,j,k} 表示考虑了前 i 位,放了 j 个 1 ,实际上 S 中有 k 个 1 的答案。但我们实际上还要额外处理进位,而不同进位情况对应的状态显然应该不同所以把往下一位进了多少也丢状态里,然后直接转移即可。这里为了方便处理,选择用自己更新后面,故枚举这一位上放的 1 的个数 x 有转移方程:
dp_{i,j,k,l}v_i^x\text{C}_{n-j}^x\to dp_{i+1,j+x,k+(l+x\bmod 2),\lfloor\frac{l+x}{2}\rfloor}
根据状态的定义显然有初始状态 dp_{0,0,0,0}=1 ,答案为所有满足 k+\text{popcount}(l)\le K 的 dp_{m+1,n,k,l} 之和,记得取模。由于复杂度比较极限所以组合数需要预处理,有递推式(建议直接背下来):
\text{C}_n^m=\text{C}_{n-1}^m+\text{C}_{n-1}^{m-1}
其中 \text{C}_i^0=1,\text{C}_0^i=0 (后者 i>0 )。
C - P7962 [NOIP2021] 方差
笔者比较菜,花了不少时间理解转移方程,遂在此展开解释了转移方程。
注:本题差分数组的最后一项显然是没有意义的,所以本题解中涉及差分数组均无视最后一项。
这种让你操作的题可以先试着找操作到底在干什么。其实就是交换差分数组的两项:
设原数组中一个长度为 3 的子段 a_1,a_2,a_3 的差分数组是 d_1=a_2-a_1,d_2=a_3-a_2 。
对 a_2 进行操作所得 a_2'=a_3+a_1-a_2 。
于是新的差分数组 d_1'=(a_3+a_1-a_2)-a_1=a_3-a_2=d_2,d_2'=a_3-(a_3+a_1-a_2)=a_2-a_1=d_1 ,即将 d_1 与 d_2 进行了交换。
考虑到方差是每个数与平均值之差 的平方的平均值,显然差分数组中一个值越靠边,其贡献次数就越少,所以接着很显然的思路是把大的靠边放。(根本用不着题解区大坨式子证明,可以画数轴理解)
现在问题在于差分数组的每个值应该放在“中间”的左边还是右边。作者数学很差不会推式子,遂抄了题解的式子:
ans=n\sum_{i=1}^na_i^2-\left(\sum_{i=1}^na_i\right)^2
设 dp_{i,j} 表示在放第 i 个差分值(升序),a 数组已填放部分之和为 j 的最小平方和。
为了方便计算,状态中计算的和及最小平方和均只包含已经填入的部分。显然填入的部分是中间的一段。
如果将 d_i 放在左侧,则已经填入的 i 个数均会受到 d_i 的影响(但新填入的数显然不会,因为它在 d_i 左侧)所以要把已经填入的数都加上 d_i ,有(设已填入的 a 值为 a'_1,a'_2,\dots,a'_i ):
\sum_{k=1}^{i}(a'_k+d_i)^2\to dp_{i+1,j+id_i}
完全平方展开 (a'_k+d_i)^2 得:
\sum_{k=1}^i(a'_k)^2+\sum_{k=1}^i2a'_kd_i+\sum_{k=1}^id_i^2\to dp_{i+1,j+id_i}
代入 \displaystyle\sum_{k=1}^{i}(a'_k)^2=dp_{i,j},\sum_{k=1}^{i}a'_k=j :
dp_{i,j}+2jd_i+id_i^2\to dp_{i+1,j+id_i}
如果将 d_i 放在右侧,则已经填入的 i 个数不受影响,而新填入的数受前面所有 d_i 的影响。故有:
dp_{i,j}+\left(\sum_{k=1}^i d_i\right)^2\to dp_{i+1,j+\tiny\displaystyle\sum_{k=1}^i d_i}
其中 \displaystyle\sum_{k=1}^i d_i 可以直接开个变量记录实现 O(1) 转移。
然后每个 dp 值取能转移到的状态里的最小值即可。初始状态 dp_{1,0}=0 ,答案在所有的 n\cdot dp_{n,j}-j^2 中取最小值,总复杂度 O(n^2V) ,不能过题。
观察最后两档数据范围发现出题人明示我们写 O(nV^2) ,而题中给出的原数组是单增的故最多只有 V 个非 0 的 d_i ,显然根据转移的原理 d_i=0 可以直接无视,于是直接从不为 0 的位置开始转移就实现 O(\min\{n,V\}nV) 了。
D - P7963 [NOIP2021] 棋局
其实感觉这把还是 D<C至少思维上 D 是容易想出来的你说是不是吧(逃)。
首先题意说明我们要维护 3 类边组成的连通块。但是加入点后会导致连通块分裂,维护难度大增。故考虑时间倒流,删除点,于是连通块分裂变为连通块合并。对于连通块,我们需要维护:
其包含的点数
其上黑子不高于某一等级的数量
其上白子不高于某一等级的数量
显然后两者是权值线段树,第一个是并查集,于是直接并查集合并+线段树合并就做完了。
然后考虑由 2 类边组成的连通块。这样的连通块是横平竖直的。所以我们可以分别维护横向和纵向的并查集,解决问题。
现在考虑 $1,2$ 类边和 $3$ 类边重复的情况。注意到 $1$ 类也可以视为横平竖直的连通块,故分别按行按列开线段树维护 $3$ 类连通块实现区间查询某连通块某行某范围内有多少个点的功能,然后跟着其他信息一起维护就做完了。
## CSP-S 2022
### A - P8817 [CSP-S 2022] 假期计划
- 知识点:(类)Meet-in-the-middle。
注:对于一条形如 $1\to x\to y$ 的路线(其中 $x$ 在 $1$ 的 $k+1$ 邻域内,$y$ 在 $x$ 的 $k+1$ 邻域内),后面称之为一条**半路线**,$x$ 称之为该半路线的**中转点**,$y$ 称之为该半路线的**终点**。
首先预处理 $k+1$ 邻域(注意到 $2500\times2500$ 的 `bool` 数组只需要不到 $6\text{MB}$)后纯纯大暴力复杂度 $O(n^4)$,不能接受。
注意到纯纯大暴力复杂度的指数除以 $2$ 后可以通过,遂考虑 Meet-in-the-middle,从枚举路线变为枚举半路线。则显然一条完整的环线是两个半路线拼起来,而能不能拼就是看这两个半路线的终点是否互为对方 $k+1$ 邻域内的点,以及两半路线是否共用除 $1$ 外的点。如果能快速地求出所有能拼的半路线的权值最大值,是不是就做完了?
但是半路线似乎是有 $O(n^2)$ 条的。所以即使真的存在一些能快速实现这种东西的 DS 科技,你的复杂度也带上了至少一个 $\log$,但 $n^2\approx6\times10^6$ 已经不宽裕了,于是通过实为困难。难道这个思路不能接着走了吗?
注意,我们刚才说的是,两个半路线能不能拼,就是看**这两个半路线的终点是否互为对方 $k+1$ 邻域内的点**。这意味着,忽略少数共用点的情况,能不能合并**与谁是中转点半毛钱关系没有**。而我们求的又是半路线的最大值,所以同样终点的半路线只有权值和最大的那条是有意义的。于是有效的半路线条数从 $O(n^2)$ 降至 $O(n)$,复杂度是可接受的。
然后判断共用点的情况。做题经验告诉我们,**删少量情况求最值时,如果最多会删 $x$ 种,就记录前 $x+1$ 最值**。分析共用点的情况在特判掉相同终点后包括:
- 共用中转点的情况
- 一个的中转点是另一个的终点的情况
所以极端情况下最大值会被删掉两种情况,于是我们维护每个终点的前三大半路线及其中转点,然后枚举终点对的时候若两点互为对方 $k+1$ 邻域内的点,则直接暴力枚举两点分别取第几小,如果没有共用点就判断能不能更新答案即可……**吗**?
你会发现把维护前三大改维护前两大照过不误。但其实是数据水了(不知道我的工单会不会有管理看 ww)。有 hack:
```
5 7 0
4 3 2 3
1 2
1 3
1 4
2 3
2 5
3 5
4 5
```
显然应该输出 `12`,只维护前两大输出 `7`。
所以这个题做完了,复杂度 $O(n^2)$。
### B - P8818 [CSP-S 2022] 策略游戏
- 知识点:线段树。
显然若 $x$ 确定,则:
- 若 $A_x$ 非负,则 $y$ 一定是给定区间内使 $B_y$ 最小的 $y$;
- 反之,则 $y$ 一定是给定区间内使 $B_y$ 最大的 $y$。
分别求出给定区间内 $B_i$ 的最小值 $a$ 和最大值 $b$。讨论:
- 若 $a\ge 0$,$A_i$ 直接选最大;
- 若 $a<0,b\ge 0$,根据上述选 $y$ 的方案,应该分别找 $A_x$ 能取到的正数负数里绝对值最小的,并求出哪个更优。
- 若 $b<0$,$A_i$ 直接选最小。
上述所有过程都可以对 $A,B$ 分别建权值线段树搞定。
### C - P8819 [CSP-S 2022] 星战
- 知识点:哈希。
口嗨过一车哈希,但这个是真正写了的第二道紫哈希。
首先可以实现反攻的标准是,所有点出度均为 $1$ 且均在一个环上。即图是由若干个至少二元的环构成的。
于是每个点只会有恰好一条入边、一条出边。
所以将所有边的终点进行集合哈希,恰好等于全集时即为 `YES`,反之为 `NO`。
我直接随机了十个二次函数 $a_{i,1}x^2+a_{i,2}x+a_{i,3}$ 进行集合哈希,采用自然溢出,可过。
:::info[相似题目推荐]
- [P5270 无论怎样神树大人都会删库跑路](https://www.luogu.com.cn/problem/P5270)
- [P10785 [NOI2024] 集合](https://www.luogu.com.cn/problem/P10785)
:::
### D - P8820 [CSP-S 2022] 数据传输
- 知识点:倍增、DP。
**作者数学很差,所以不讲 DDP。**
上来的暴力思路是,$k$ 邻域内所有点之间建边,查询变求最短路。
这可能会导致边数变得巨大,比如菊花图 $k>=2$ 时喜提建了个完全图。所以需要优化边数。
注意到其实原需求就是两做贡献的点间最多隔着 $k-1$ 个不贡献的点。遂直接分 $k$ 层第 $i$ 层表示这是连续第 $i-1$ 个没计入答案的点就做完了。于是开始优化。
考虑到此题是树上路径查询,先给倍增 LCA 搞里头。
然后树上路径问题最省事的方法是树上差分。至于为什么不是前缀和因为我们大胆猜测最短路是可以减的,直接树形 DP 求出走到 $1$ 的最短路然后减就做完了……吗?
我们发现其实不能减,因为 $s$ 到 $1$ 的最短路径不必然使 $s$ 与 $t$ 的 LCA 做贡献。
但是我们又发现虽然 LCA 不必然计入贡献,但它不管怎么说是必然在 $s$ 到 $t$ 的路径上的,所以我们想到可以沿用开始时建点的思路,DP 时也容易了,直接设 $dp_{x,i,y,j}$ 表示第 $i$ 层 $x$ 号点走到第 $j$ 层 $x$ 的 $2^{y}$ 级祖先对应点的答案,转移时只需要先转移 $dp_{x,i,0,j}$ 且为了方便后期合并 $x$ 自身贡献一律不算进 $dp$ 值中(后面算路径的时候单独加一下),故有几种可能:
- $x$ 和其父亲都不贡献答案,有 $dp_{x,0,0,1}=dp_{x,1,0,2}=0$。
- 其父亲贡献答案,$dp_{x,0,0,0}=dp_{x,1,0,0}=dp_{x,2,0,0}=v_{fa_x}$。
- 其走到其附近点权最小的点,再走到其父亲,$dp_{x,2,0,2}$ 为该点权。
后面 $j\neq0$ 的部分像 LCA 里处理 $fa$ 数组一样根据 DP 状态分别枚举所涉及的三个点(较低链较低点、较低链较高点或者较高链较低点、较高链较高点)所在的层进行合并即可。
然后我们分别枚举 $s,t$ 走到 LCA 时 LCA 的状态(即刚才分层图中的 $0/1/2$ 层)并合并答案,设二者分别枚举 LCA 在第 $i,j$ 层,则:
- $i=j=0$ 时 LCA 算重,需要减去 $v_{\text{LCA}}$。
- $i=j=k-1(k\neq1)$ 时无法直接跨过 LCA,需要找 LCA 附近点权最小的点作为中转点,加上该点点权。
- 其他情况可以直接合并路线。
算完了。复杂度 $O(k^3n\log n)$。
## NOIP 2022
### A - P8865 [NOIP2022] 种花
- 知识点:无。
虽然语言比较~~犯病~~稚嫩,但作为小蒟蒻第一篇过审的题解+第一个独立完成的绿题决定还是不动了(不过删掉了部分过于啰嗦的东西及格式问题),权当留个纪念。所以如果写得不清楚欢迎撅我。
#### Part1 题意
一个 $n\times m$ 的方格,其中有一些格不能种花。求在能种花的格子里种 $\texttt{C}$ 形及 $\texttt{F}$ 形的方案数。$\texttt{C}$ 形及 $\texttt{F}$ 形的定义如下:
- $\texttt{C}$ 形要有两横一竖,其中“横”的长度不要求相等但至少是两格;“竖”的长度至少是三格。
- $\texttt{F}$ 形就是在合法的 $\texttt{C}$ 形的“竖”底下加一段。
#### Part2 注意点
- 两种**不**合法的情况:
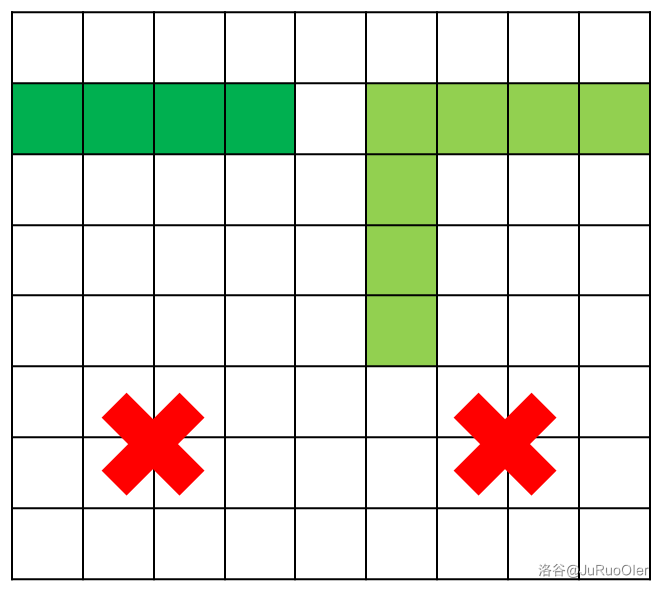
- **重合型**:即两横重合,如图(深绿色是 $\texttt{C}$ 的错误示范,浅绿色是 $\texttt{F}$ 的错误示范)。
- 
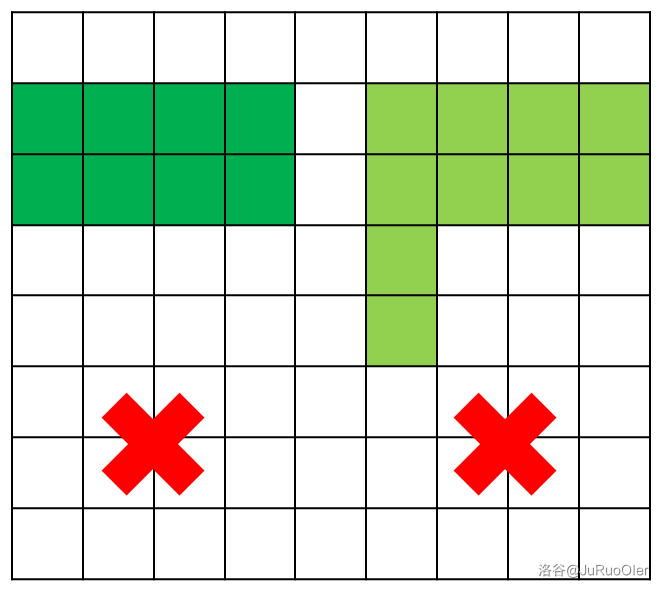
- **相邻型**:即两横相邻,如图(深绿色是 $\texttt{C}$ 的错误示范,浅绿色是 $\texttt{F}$ 的错误示范)。
- 
- 注意本题单个测试点内有多组数据。多测不清空,爆零两行泪。同时请注意换行。
- 注意输出时先乘给定常数再取模,取完模输出。
#### Part3 $\text{O}(n^2m^2)$ 暴力做法
对于每一个格子,暴力找以这一格为左上角的所有可能性,一个个累加结果。时间复杂度 $O(n^2m^2)$。具体过程:
- 先找这一格往右有多少格;再从这一格向下走,从它下面的**第二格**(第一格会变成上文的“相邻型”)开始每格向右找,累计每行的格子数,最后乘开始那格往右的格数就是 $\texttt{C}$ 形的数量。$\texttt{F}$ 形还要乘上可以作为竖的格子数。
- 样例一中计算过程如图,其中 $\texttt{C}$ 形计算的两个因数分别是首行可选长度数和该行可选长度数,$\texttt{F}$ 形计算的前两个因数与 $\texttt{C}$ 形一致,最后一个因数是后面剩余的可作为竖的行数。
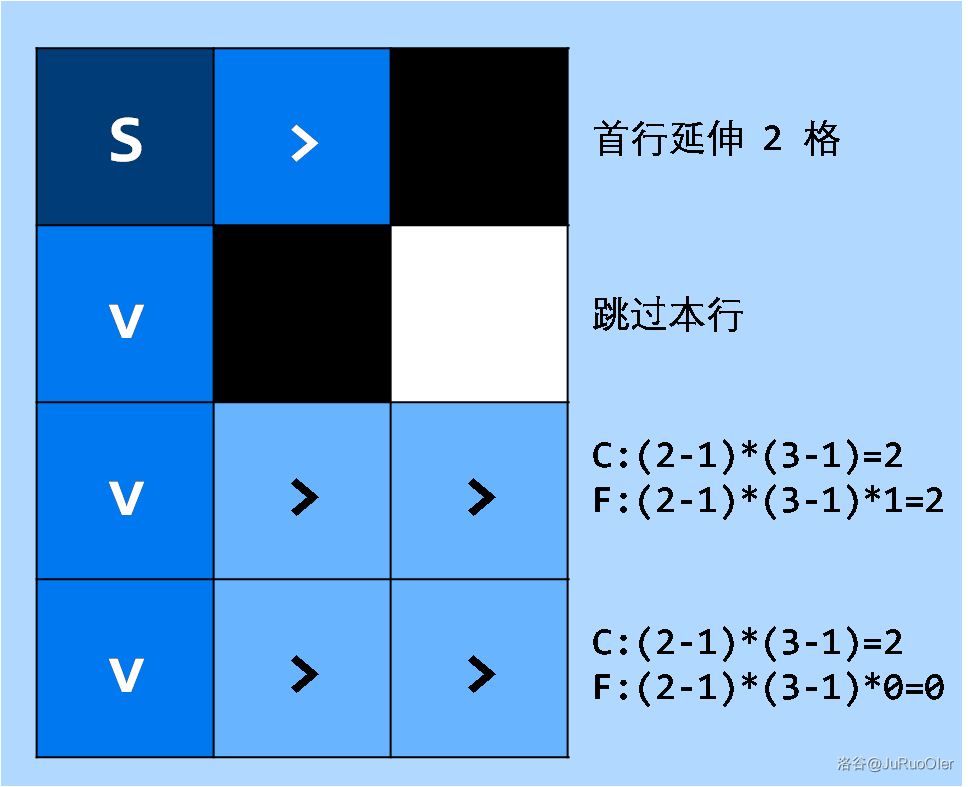
#### Part4 如何优化到 $\text{O}(nm)$?
显然,$\text{O}(n^2m^2)$ 的做法最多只有 $39$ 分。依据数据范围,可以猜出,想通过就必须要 $\text{O}(nm)$。
可以发现在上面的图中,每个位置可向右延伸的格数会被算多次。我们就不能用 $\text{O}(nm)$ 的时间把每个点向右及向下到不能种花的位置的格数预处理出来吗?
显然是可以的。从右往左、从下往上一个个计数即可。例如样例第一列统计得:
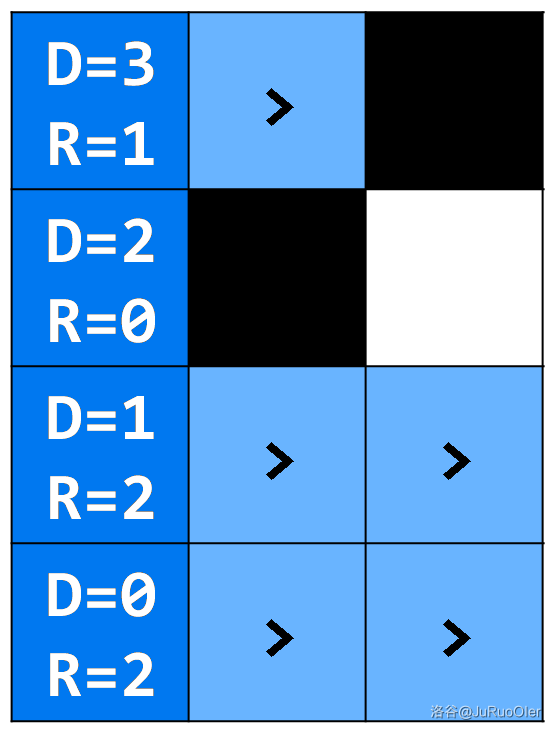
这样复杂度就变成了 $\text{O}(n^2m)$。
接着考虑,为什么非要枚举左上角,每次从上往下找呢?直接枚举第二横与竖的交点,就可以边枚举边计数,不需要每次都重新算上面的可能性有多少了。这样,我们的代码就变成了 $\text{O}(nm)$。
### B - P8866 [NOIP2022] 喵了个喵
- 知识点:Ad-hoc
首先注意到 $n=2(k-1)$ 的点放到了送分的位置,估计是没啥难度。
于是注意到最坏情况下前 $k-1$ 个栈可以使每种元素都出现在某栈顶部或底部,而且此时还空出了一个栈。然后就搞定了。然后开始大战多出的那个元素,也就是说我们面对的是变成前 $k-1$ 个栈有 $2(k-1)$ 个互不相同的元素而牌堆顶和这 $2k$ 个都不同的局面。
首先我们显然不可能给多出来那个元素放空栈里,因为这样会直接导致如果下一个是栈底就被封死了。于是为了解决这个问题我们直接开透视,找到下一个不是栈顶的元素(如果某一个元素重复来也不要紧,给它安排那个固定位置即可)。
- 如果这个元素就是我们刚才多的那个,那么可以放心地把多的那个放空栈里;
- 如果这个元素不是我们刚才多的那个,那么它显然是某个栈的栈底,此时看该栈栈顶是否被消去了,如果没有就把刚才多的放上去,消去了就把多的放空栈里,然后把这个栈变成新的空栈。
这个过程是容易维护的于是做完了。复杂度 $O(m)$。
在题解区看到了一个很好的思考方法:
>如果游戏更改一下规则,玩家必须在读入每个图案后就立即决定该图案应该放进那个栈里。
>
>那么 $k=2n-1$ 时很有可能玩家是必败的。这也启示我们在作当前决策时必须考虑之后的图案。考虑到这一点后本题就不是特别棘手了。
>
>——@[周子衡](https://www.luogu.com.cn/user/112794)
### C - P8867 [NOIP2022] 建造军营
- 知识点:树形 DP、边双连通分量。
读题:B 只会攻击**一条**边。~~这个人以为所有没看守的边可能同时被攻击然后不到一上午其实就做完了但愣是又凹了一下午+一晚上直到看了第一篇题解的第一句话……~~
由于 B 只会攻击一条边所以首先非割边防不防没啥区别。于是缩点变成一棵树。
由于是计数题考虑树形 DP。然后经过/不经过一条边的选点方式是经典问题了:
- 经过即子树内和子树外至少各选一点;
- 不经过即仅子树内任选或者仅子树外任选(本题按题意至少选一点)。
但只拿着这个玩意是算不了答案的,因为又有子树内又有子树外,多条边的答案很难不重不漏地合并。
所以为了方便合并我们直接钦定只能取子树内的点。设点 $i$ 缩点前对应 $v_i$ 个点、$e_i$ 条边,$i$ 的父亲为 $fa_i$,以 $i$ 为根的子树内选 $(i,fa_i)$ 这条边的答案为 $f_i$,以 $i$ 为根的子树内的总边数(含被缩掉的边)为 $sz_i$ 条,则:
- 一个点 $x$ 对其父亲 $y$ 的贡献有三种可能,一种是选择边 $(x,fa_x)$,一种是不选该边但在子树内选点,一种是不选该边且不在子树内选点,其中最后一种不需要记录因为它显然等于 $2^{sz_i+1}$。
- 第一种可能允许多个儿子同时选择,且允许在 $y$ 上选任意多个点,而不选择这种可能的点则只能选择第三种可能(因为子树外面已经选点了),故这种情况下 $f_y$ 会获得 $2^{v_y+e_y}\cdot\displaystyle\prod_{x\in son(y)}(f_x+2^{sz_x})$ 的总贡献;
- 第二种可能只允许恰好一个儿子选择,且不允许在 $y$ 上选点,而选中边 $(x,y)$ 的情况在上一种可能中其实已经被计算了所以边 $(x,y)$ 不做贡献,故这种情况下 $f_y$ 会获得 $2^{e_y}\cdot\displaystyle\sum_{x\in son(y)}2^{\tiny\displaystyle\sum_{z\in son(y),z\neq x}(sz_z+1)}\cdot f_x$ 的总贡献。
- 但仔细分析,上述过程其实有问题:对于只在一个 $x$ 内选点的情况,我们仍然认为边 $(x,y)$ 选法任意,但不选该边的情况其实是不能更新 $fa_y$ 或以上点的,所以应该分开计算,即 $f_i$ 改为只计算 $i$ 与 $i$ 子树内所有选了的点能通过选了的边连通的方案数,而另设 $g_i$ 表示在 $i$ 子树内选点,选了的点间可以仅通过选了的边连通,但 $i$ 不能仅通过选了的边与选了的点的连通的方案数。说白了其实就是 $f_i$ 允许 $i$ 接着选点而 $g_i$ 不允许。此时转移是:
- 第一种情况不变;
- 第二种情况不再对 $f_y$ 贡献,而是对 $g_y$ 做 $2^{sz_y-e_x-1}(f_x-2^{sz_x})+2^{sz_y-e_x}g_x$ 的贡献,其中 $-2^{sz_x}$ 是去掉了光选边的情况。
答案即 $f_1+g_1-2^{sz_1}$,这里 $1$ 是钦定的根节点。复杂度线性。
### D - P8868 [NOIP2022] 比赛
- 知识点:线段树。
注:写题解的时候思路还是不是很清楚,如果看不懂题解在说什么可以去看视频。
完全暴力枚举子区间并暴力找最大值,总复杂度 $O(qn^3)$,期望得分 $8$。如果求区间最大值的时候上个数据结构,复杂度变为 $O(qn^2\log n)$,或者合理规划枚举顺序直接复用最大值做到 $O(qn^2)$,但得分都没啥区别。
发现每个值贡献多少个子区间是固定的,拿个单调栈预处理出每个数左侧/右侧第一个比它大的数的位置即可得到它贡献的子区间数,然后注意到分别将所求区间中 $a,b$ 中各数与其贡献的子区间数乘积求和得 $s_a,s_b$,则原式 $\displaystyle\sum_{p=l}^r\sum_{q=p}^r\max_{i\in[p,q]}\{a_i\}\cdot\max_{i\in[p,q]}\{b_i\}$ 其实就等价于 $s_a\cdot s_b$,而按照刚才求 $s_a,s_b$ 的算法这个过程的复杂度是 $O(n)$ 的,总复杂度压到了 $O(qn)$,可以获得 $52$ 分。而且我们成功地省去了枚举子区间,这通常是解决对所有子区间求和类数据结构问题的重要步骤。
但上述做法难以实现区间合并,也就难以上树维护。考虑另外的容易维护的暴力算法:将询问离线并按 $r$ 的值排序,然后我们记 $f_i$ 为以当前 $r$ 为右端点、$i$ 为左端点的子区间的贡献,则 $f_i=\displaystyle\sum_{j=i}^r\max_{k\in[j,r]}\{a_k\}\cdot\max_{k\in[j,r]}\{b_k\}$,而询问 $[l,r]$ 的答案就是 $\displaystyle\sum_{i=l}^rf_i$。这种算法每次向右移动 $r$ 时暴力更新各 $f_i$ 的复杂度是 $O(n^2+nq)$,然后把 $f_i$ 挂到树上可以变成复杂度 $O(n^2+q\log n)$ 的单点修改区间求和,得分只有 $20$。
现在就是怎么把 $n^2$ 优化掉。注意到我们提出的第一个 $52$ 分做法中利用了每个 $a_i$(为例,$b_i$ 同理)贡献的区间连续的性质,故考虑沿用这种方法,用单调栈预处理每个 $a_i$ 的贡献范围的左端点,就可以首先实现快速维护各后缀的 $\max$ 值。即设 $x_j=\displaystyle\max_{k\in[j,r]}\{a_k\},y_j=\max_{k\in[j,r]}\{b_k\}$,则原询问变为:
- 对 $x$ 进行区间赋值
- 对 $y$ 进行区间赋值
- 将 $f$ 区间加 $x_iy_i
发现这个问题是一个二维历史和,作为完整研读过吉司机线段树原论文但其实啥也没学到的选手当然要申请出战:吉司机讲了一维的历史和,其本质是用矩阵维护区间长度、和和历史和;类比探究一下,用矩阵维护区间长度、\sum x_i 、\sum y_i 、\sum x_iy_i 及该区间历史和,然后根据定义可以得出转移矩阵,这里作者懒得推了(实际上是数学太差)贴个题解区的:
但是部分选手声称其使用这种做法常数太大被做局了,于是我们可以不用矩阵但保留上述思路,即拿标记维护 \sum x_i 、\sum y_i 、\sum x_iy_i 及该区间历史和,并另拿标记维护赋值操作和对区间长度、\sum x_i 、\sum y_i 和 \sum x_iy_i 加的倍数然后对着上面矩阵抄式子就完事了。
总复杂度 O((n+q)\log n) 。
春季测试 2023
讲这场的原因是很多省份将它作为 NOIP 2022(因为疫情),甚至有传言称这才是真正的 NOIP 2022 试题。
不过统计 22 年知识点构成的时候还是按 NOIP 2022 计算,毕竟这两场强度差得有点大。
送分题不讲。
B - P9118 [春季测试 2023] 幂次
看数据范围,首先注意到:
暴力是 O(\sqrt[k]{n}\log n) (远不满)的,即 k\ge3 时可以直接暴力。
于是现在唯一的问题是 k=2 。一种思路是直接加个 \sqrt{n} ,但这样显然会算重。
考虑算重的情况是什么样子的。其实就是存在 c=a^p=b^q 的情况。此时不妨设 a<b ,则必然有 b=a^k ,因为否则若干个 a 相乘不可能出来一个 a 以外的因数,也就不可能实现 a^p=c 。
于是根据刚才 k\ge3 的算法,从小到大枚举 2\le i\le\sqrt[3]{n} ,若 i 还未标记则标记其在 \sqrt[3]{n} 内的所有幂次并记录其在 (\sqrt[3]{n},\sqrt{n}] 内幂次的个数 s 。则 (\sqrt[3]{n},\sqrt{n}] 内未被计算的数的个数就是 \lfloor\sqrt{n}\rfloor-\lceil\sqrt[3]{n}\rceil-s ,加上刚才暴力的结果即可。
注意用 sqrtl,否则会 WA on #21。
C - P9119 [春季测试 2023] 圣诞树
这题挺容易读成求最小生成树的。其实是要求以最高点为开头的一条链。
性质是电线不交叉的情况一定更优,可以用三角不等式证。
而题中本来就是按照凸包顺序给的,所以其实每次就是在现有区间往左或往右选。
于是考虑区间 DP,设 dp_{i,j,0/1} 表示考虑区间 [i,j] 且上一个选择了 i/j 的答案。根据状态定义进行转移:
dp_{i,j,0}=\min\{dp_{i+1,j,0}+dis(i,i+1),dp_{i+1,j,0}+dis(i,j)\}\\dp_{i,j,1}=\min\{dp_{i,j-1,1}+dis(j,j-1),dp_{i,j-1,0}+dis(i,j)\}
轮换一下,把最高点转到最左边就行了。复杂度 O(n^2) 。
D - P9120 [春季测试 2023] 密码锁
与 CSP-S2 2023 遥相呼应。但一个 T1,一个 T4。
最值问题与计数问题不同,各板块都有很多算法都可以求解一类特定的最值问题。所以此时我们只能通过题目中给出的提示进一步确定答题方向。我们采用审政治题的思路:
一审设问:
本题要求最大值的最小值。学过二分的同学都知道,“最大值最小”“最小值最大”类问题可能是二分答案。
本题数据范围里 k 很小。由于 n 较大,且 k 的数据点分布与 T2 类似,任意 k\in[2,4] 都有一定量的点,所以较大可能是和 T2 一样对着 k 讨论。
二审材料:
经历了上述过程之后,我们发现:
$k=4$ 与 $k=3$ 区别在于多了一行不确定的值。但不变的是枚举最值所在行后剩下两行的取值集合只有不超过 $4$ 个,而每对取值经过上述转化后可以得到两个区间。由于区间之间有对应关系,将两个区间分开显然是不现实的,于是只能做矩形加,外面套一层容斥来解决重叠(所以最后还是矩形加)。然后你发现这题变成了 [P1502 窗口的星星](https://www.luogu.com.cn/problem/P1502),然后本题就做完了。
以防你没做过扫描线的题:
- 对每个矩形的左右边界找出其纵坐标的范围和权值(左边界记权值,右边界记权值的相反数)。
- 将各边界排序,对纵坐标建立线段树,上述操作就是区间加、区间取 $\max$ 的过程。
- 扫描线题都要注意处理好边界计算的顺序。
---
收录一下最高赞题解@[AL8624](https://www.luogu.com.cn/user/913226) 大佬的做法:
考虑枚举每个环并对当前环贪心。这显然是错的。
但是发现打乱 $600$ 次就很可能对一次。于是打乱 $600$ 次做即可。
为了避免被卡常 $k\le 3$ 可以只打乱 $300$ 次。
调整合理的种子后可过。
## CSP-S2 2023
送分题及大模拟不讲。
### B - P9753 [CSP-S 2023] 消消乐
- 知识点:哈希。
注意到这玩意本质上是不分左右的括号匹配,所以两次相同的未匹配栈状态之间的部分必然匹配。
于是用哈希维护当前的栈状态然后开个 `map` 统计一下每种状态多少个然后用组合数在每种状态里选两个所有状态加起来就做完了。
用 `map` 带个 $\log$,换成 `umap` 线性,都能过就是了。
注意空栈和单个 `a` 的区分。
### D - P9755 [CSP-S 2023] 种树
- 知识点:二分答案。
对于一个固定的总用时,容易求出每个位置的 ddl(最晚哪一天种植);又注意到总用时有单调性,遂考虑二分。
`check` 时每次找 ddl 最靠前的,把从根结点到该点路径上依次种上树,如果哪次没在 ddl 之前种上就是 `false`,都种上了就是 `true`。
复杂度 $O(n\log^2 n)$。
## NOIP 2023
送分题不讲。
### B - P9869 [NOIP2023] 三值逻辑
- 知识点:并查集。
注意到每个位置最终只可能是定值、某个初值或者某个初值取反。故先处理出来每个值的最终状态是什么,然后先处理两种一定是 U 的情况:
- 定值是 U 的;
- 自己初值取反的。
然后再把别的扫一遍,看有没有最终状态是某个初值为 U 的或者某个初值为 U 的取反的,来看自己是不是也需要赋值为 U。
写完发现过不了大样例。调试发现因为可能会间接连到一个初值为 U 的。例如依次有 $x_9\to x_2,x_{10}\to x_9,U\to x_{10}$ 三种操作,则你只确定了 $x_9,x_{10}$ 为 U,而没能确定出 $x_2$ 为 U。
发现将这种关系改为并查集维护,将 $x_i$ 与 $x_i$ 取反分成两个点即可(其他实现也没问题,重点在你写的时候保持思路清晰)。复杂度视并查集的实现而定,$O(n\log n)$ 即可过题。
### C - P9870 [NOIP2023] 双序列拓展
读题,题中给的合法的定义其实就是拓展完后一个偏序另一个。不妨设 $\forall i,x_i<y_i$,反之可以交换 $x$ 和 $y$(根据语言基础时期讲的“指针可以当成数组名”知可以定义两个指针从而实现 $O(1)$ 交换),一些题解里巧妙地选择了将 $x$ 与 $y$ 同乘 $-1$ 也是很好的。
手玩大样例发现题意又可以视为 $x$(或者 $y$,合法情况至少有一个可以)中的一个元素匹配 $y$ 中的一段然后反过来 $y$ 的下一个元素匹配 $x$ 中一段,直至两边都匹配完。显然有暴力 DP:设 $dp_{i,j}$ 表示 $x_1\dots x_i$ 匹配 $y_1\dots y_j$,直接 $O(1)$ 地往下一项转移即可,单组复杂度 $O(n^2)$。
>实际上由于这个 dp 状态维度过高且难以优化,自然可以考虑贪心。
>
>:::align{right}
>——@[_yjh](https://www.luogu.com.cn/user/222104)
>:::
我们枚举 $x_i$,同时维护一个指针 $p$ 维护当前 $x_i$ 可匹配到的右边界,如果 $x_i<x_{i-1}$ 则范围会变大,向右移动 $p$ 直至不合法或到边界;反之向左移动 $p$ 直至该边界合法即可。若最后 $p$ 能移到右端点则可以,否则不行。上述结论我做的时候是猜出来的,下面贴题解的证明:
>
>
>:::align{right}
>——@[_yjh](https://www.luogu.com.cn/user/222104)
>:::
移动指针的过程可以线段树上二分优化到 $1\log$。还没试,有卡常大哥哥可以写一发,据说本题 $O(qn^2)$ 都能跑 $70$。
综合上述做法与特殊性质的提醒,不难想到关注最小值的位置。注意到只有前缀最小值会使指针往右移动,故两前缀最小值之间的部分只需要看最大的会不会跑到最左边。
然后将序列按全局最小值分开前一半跑一遍后一半倒着跑一遍就做完了。
### D - P9871 [NOIP2023] 天天爱打卡
- 知识点:线段树优化 DP。
纪念下第一次独立想出线段树优化 DP。难度评分也主要是线段树优化 DP 带起来的。
数据范围已经提示了让你把挑战看成区间。显然不浪费打卡天数的方式必然是打卡若干段,每段是从某个挑战的左端点到某个(不一定和前面相同)的挑战的右端点之间的所有点。
设 $dp_{i,j}$ 表示考虑到 $r_i$ 且 $[l_j,r_i]$ 进行打卡,可以暴力转移,复杂度 $O(m^2)$。
考虑优化。对于一个 $r_i$ 考虑所选的 $l_j$,则显然此时满足 $l_j\le r_i$ 的 $j$ 分为三段:
- $l_j\in[1,r_i-k]$:这些起点无法一直打卡到 $r_i$,不能转移。
- $l_j\in(r_i-k,l_i]$(如果有):这些起点可以一直打卡到 $r_i$,且可以达成挑战 $i$。
- $l_j\in(max\{l_i,r_i-k\},r_i]$:这些起点可以一直打卡到 $r_i$,但不能达成挑战 $i$。
这里视频漏掉的一个点是 $l_i$ 上值的更新问题,视频里直接就说拿 $dp$ 值了,实际上为了正确计算消耗应该对所有 $l_i$ 和 $r_i$ 放在一起排序,每段更新一次后两类区间的消耗,然后对于每个 $r_i$ 再把第二段加上第 $i$ 个挑战的贡献,这样才能准确统计答案。
最终答案对所有的 $dp_i$ 取 $\max$。复杂度 $O(m\log m)$。
## CSP-S2 2024
送分题不讲。
### B - P11232 [CSP-S 2024] 超速检测
- 知识点:贪心。
第一问他甚至没舍得让你离散化($L\le 10^6$)。直接对探头做个前缀和,用公式求出每辆车的超速区间即可。
第二问先找到所有有探头的区间并按左端点排个序,如果一个区间包含另一个则这个区间显然是没有用的(因为另一个里显然得包含一个探头,那这个肯定也就包含该探头)于是去掉这种的之后右端点也自动排好序了。然后从左往右枚举区间,每次贪心地找区间内最靠右的探头(如果这个区间已经选过探头了就跳过)来覆盖尽可能多的区间然后就做完了。
写代码的时候仔细点要不然一些小的 corner case 极其难调。本人考场上调了 3h 最终喜提没时间做 T3 了。
### C - P11233 [CSP-S 2024] 染色
- 知识点:普通 DP。
设 $dp_{i,0/1}$ 表示考虑到第 $i$ 个数且该数染红色/蓝色的答案。
则如果不想让 $i$ 贡献直接从 $i-1$ 转移,反之一定是取上一个与 $a_i$ 相同的数最优,设该数位于 $lst$,则贡献分为:
- $a_i$ 的贡献。
- $[1,lst+1]$ 的贡献。这部分直接取 $dp_{lst+1}$ 的最大值即可。
- $[lst+2,i-1]$ 的贡献。这部分是同色的,可以使用前缀和进行优化。
总复杂度 $O(n)$。
### D - P11234 [CSP-S 2024] 擂台游戏
- 知识点:无。
下称题目中补充的选手为“自由人”。
#### 暴力算法
分别钦定每一个人赢,然后试图构造这样的方案。
思考两个问题。
首先:**规则中有什么值得注意的点?**
- 我们发现,虽然是擂台游戏,但胜负与攻擂者居然无关。这意味着,题中判断胜负的方式很可能具有某种特殊性质。
从写暴力的角度,为了判断胜负,我们提出第二个问题:**如果在某一回合中,一个选手与自由人对阵且自由人是擂主,是否可以通过控制自由人的权值来决定谁上?**
- 一定可以。这个其实乍一看感觉很有问题,因为这可能影响到其上升路径;但实际上可以分类讨论,假设我要送对面上:
- 如果上升路径中某一轮次是自由人当擂主,则由于获胜该轮比获胜我们刚才说的那轮的要求能力值低,所以一定存在这样的赋权值方法;
- 如果上升路径中某一轮次是自由人对面当擂主,则由于结果与该自由人无关所以赋什么权值自然也不影响。
这里暴力的算法就出来了:
- 枚举每个人并钦定他赢;
- 模拟各个对局,如果当前结果确定(两个自由人或者擂主不是自由人),则直接模拟;如果不确定,则如果对面不是钦定的赢家就让自由人上,反之让对面上。
总复杂度 $O(Tmn^2)$。
#### 优化一点
最明显的优化方向就是最后那个 $n^2$。要不然绕开枚举每个人,要不然快速求出每个人。
- 绕开枚举每个人的过程:记录所有可能到达当前位置的人,这样一遍 $O(n\log n)$ 就能搞定。
- 加速求出每个人的过程:其实对一个人有影响的只有他经过的 $O(\log n)$ 条路径,其他位置的信息可以复用。
无论怎么搞,至少我们可以实现 $O(Tmn\log n)$ 的优秀复杂度了。
#### 优化至 $1\log
感觉这题到现在给做死了,因为对于不同的询问,不管我们刚才采用什么样的优化方式,都会导致整个游戏过程被改变,所以难以快速地对询问进行更新。
于是剩下唯一的优化空间似乎是 m 这里。
而这个方向上,题中给出的询问每次都是一段前缀,似乎能以此入手……?
于是我们一厢情愿地希望,一个人只在 c 在一段范围内时可能获胜。
考虑二叉树形态完全相同,即 [2^k+1,2^{k+1}] 内的所有前缀中,最终的胜者会如何随前缀取值而变化。容易入手的情况是自由人获胜,这时显然的前缀越短自由人越容易上,所以最终自由人可能登顶的前缀长度肯定是有一个上界的。
考虑将二叉树加高一层时的情况。如果一非自由人能到达该层(显然此时该层左子树内必然已经没有自由人)且擂主是对面,则看对面的情况:如果对面必然上来一个非自由人时(此时谁上来是定死的)我照样能赢那显然我能赢的区间是对面一整个;反之就只能是能使对面上来自由人的一段前缀。
至此,在扫前缀的过程中,我们就可以求出每个人所贡献的前缀区间是谁,这个过程的总复杂度是 O(Tn\log n) 。
优化至线性
这里出现 \log 的原因显然是在枚举前缀的过程中自底向上走了一条长度为树高的路线,所以考虑能不能实现自顶向下,因为结点总数是 n 级别的。
考虑不再针对个人处理,而是对于每个子树,处理其在什么时候开始会有一个确定的胜者。这个过程中由于每个点只会走一遍(每个比赛只会有一人胜出并进入下一层),所以总复杂度其实是 O(n) 的。然后自顶向下根据预处理的信息,依照上述思路进行下传即可完成本题,复杂度 O(Tn) 。
启示
在看到一些比较特殊的条件时,我们应该试着寻求更加简洁的算法。
对于在变化的过程中计算贡献的问题,我们应该试着找到答案随着条件变化的方式。
NOIP 2024
A - P11361 [NOIP2024] 编辑字符串
考虑贪心,能匹配就匹配,因为我匹配这个最多只会导致另外一个不能匹配,肯定不亏。
倒着扫两个串,预处理出各可编辑连续段中 0 和 1 的数量,这样第二遍扫的时候一边扫一边能实时维护当前还有多少个 0/1 可以换。然后就做完了,复杂度线性。
B - P11362 [NOIP2024] 遗失的赋值
容易注意到不存在赋值方式的情况一定是两个一元限制之间的二元限制使得一元限制不能同时满足。这种情况下设这两个一元限制分别是 (c_1,d_1) 和 (c_2,d_2) ,则上述情况用数学语言表达就是:
也就是对于 i\in[c_1,c_2) ,只有 a_{c_1+1},\dots,a_{c_2-1} 是可以在 [1,v] 内任选的。而这段内全部的情况是,a_{c_1},\dots,a_{c_2-1} 和 b_{c_1},\dots,b_{c_2-1} 中所有的值都任选。减一下搞定一段,各段相乘搞定全局。复杂度由于有快速幂带个 \log 。
C - P11363 [NOIP2024] 树的遍历
这题整体的难度也不是很大。找到关键性质后整道题会变得很简单。
首先考虑 k=1 怎么做。
发现对于一个点,不同的遍历儿子的顺序必然导致生成 DFS 树的改变 ,因为根据题中定义一个点除了第一个遍历到的儿子连父亲之外都是其他都是连兄弟的。所以答案是 \prod(d_i-1)! ,其中 d_i 是度数(减一因为去掉父亲)。
但显然不是树上所有点都能生成这棵树,所以我们需要探究哪些点能生成这棵树。
鉴于学校机器的优秀性能(我在写这段文字的时候操作的平均延迟目测在 $100$ ms),我们去题解里偷张图来讲:
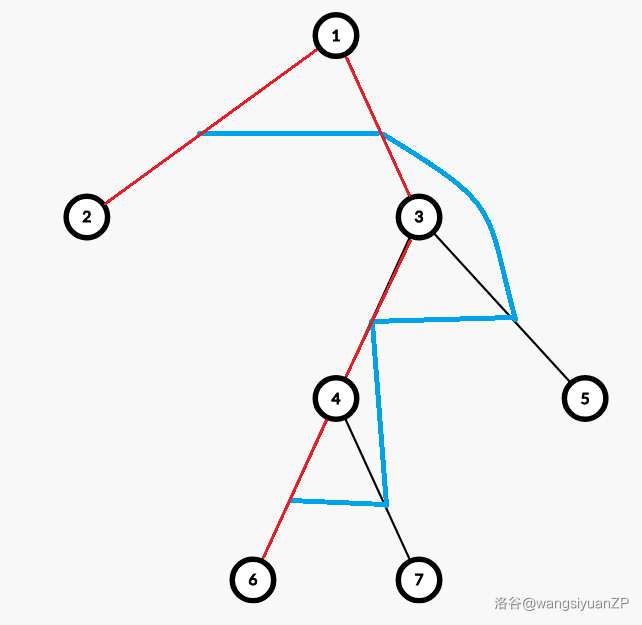
其中,蓝色边是新生成的树,红色边是可能作为根节点的原始边。
其实图都偷来了接下来的步骤就一样了。因为这个红边边集构成的链实在显眼,所以我也没法讲出朵花来,就是大胆猜想可能的根节点一定恰好是一条从原树的叶子到叶子的链。题解的证明是:
>证明也很简单,考虑一个点周围的所有黑边,这些边内部的蓝边一定是一条链,而只有链的两个端点可以作为根的方向。
要是想不明白或者考场上证不出来,你其实可以画一个三元环作为新图(对应原图是 $n=4$ 的菊花)并任取其中两条边得到一个可能的生成树,然后注意到未被选中的边两端点才能生成这棵树,于是你就理解上面那句话怎么证的了。(~~别说有时候感性理解还挺好用的~~)
于是当新图生成树形态确定的时候,这条链也就确定了,只要链上有关键边这棵生成树就贡献。而一条链可能对应多棵生成树,具体来说式子是:
$$\dfrac{\prod (d_i-1)!}{\prod (d_v-1)}$$
$v$ 是链上的点,且忽略 $d_v=1$ 的 $v$。也就是链上的点由于要保持链形态,而不能接着任选顺序了。
于是现在要快速统计所有有关键边的链的贡献。于是计数题七字真言又来了。设 $dp_{i,0/1}$ 表示走到第 $i$ 个点,当前是否有关键边的方案数,对着上面式子直接转移即可。
### D - P11364 [NOIP2024] 树上查询
- 知识点:线段树。
介绍一个我比较喜欢的做法。本题题解区里 @[Rainbow_qwq](https://www.luogu.com.cn/user/151935) 老师发了这种做法。
题外话:喜欢这个做法的原因是,其实考前我一直在研究区间维护复杂信息(P9530 之类的结点内倍增),所以考场上试图想这种做法来着,但没发现性质最终倒闭了。然后一出场看到 @[Rainbow_qwq](https://www.luogu.com.cn/user/151935) 老师的题解当时就崩了,立刻发给教练,教练一通电话就过来了,于是我们又对着这题聊了近 $1$ h 才搞定。
首先容易注意到点多了 LCA 深度是不会下降的,所以长度恰好为 $k$ 就是最优的。
性质:**对于 $k\ge 2$ 的询问($k=1$ 的直接搞个线段树什么的维护下区间 $\max$ 就行),区间 LCA 的深度其实就是区间内相邻两点 LCA 深度的最大值**。笔者没学过虚树不会证明,要不然也不至于拿到此题低于 $100$ 分的成绩。
于是问题转化为全局每相邻两数取一次 $\min$,并查询区间最值的最值。
维护所有的同深度连续段。分析一次邻数合并时一段的长度变化。显然只会在两段交界处发生变化,较小的吃较大的。于是小于两边的长度每次加 $1$,大于两边的每次减 $1$,一边大一边小的不变。然后每次段数出现变化就是在当前减 $1$ 的最短段消失时,由于最多就 $n$ 段所以直接用一个类链表的结构,维护每段两侧是谁就能快速删除。查询时线段树上二分一下即可。
:::info[相似题目推荐]
这题发现完性质之后其实就和 [AT_abc407_f \[ABC407F\] Sums of Sliding Window Maximum](https://www.luogu.com.cn/problem/AT_abc407_f) 十分像了。
:::
## CSP-S2 2025
### 唠嗑
首先观摩一下 T3 大样例的强度。
你就说 $37375$ 是不是小于 $2\times10^5$ 吧。
你就说 $2235$ 是不是小于 $2\times10^5$ 吧。
当我看到我的 $O(nq+aL)$(其中 $a$ 为巨大常数)$0.3$ 秒碾过大样例的时候我下意识打开看了一眼,然后就看到了上面这些东西。
### A - P14361 [CSP-S 2025] 社团招新 / club
- 知识点:贪心。
注意到最多只会有一个社团爆掉。
于是先让每个人去自己最喜欢的,此时多余的人可以任意调剂到另两个社团而不会使它们爆掉。
所以多余的人都可以安排到自己第二喜欢的里面。于是按最喜欢的减第二喜欢的从小往大选调剂的人。
复杂度 $O(n\log n)$ 每组。
---
当你在坚持和放弃间飘摇不定的时候,也许你就会和刚才被我们调剂的那些人一样,被命运调剂。
他们不是无辜的,因为他们的意志不够坚定。所以,寄希望于下一把能考好,也许会带来转机……?
>我们所可以自慰的,想来想去,也还是所谓对于将来的希望。
>
>希望是附丽于存在的,有存在,便有希望,有希望,便是光明。
### B - P14362 [CSP-S 2025] 道路修复 / road
- 知识点:最小生成树。
注意到直接贴板子有 $48$ pts($k=0$ 及性质 A)。
外层对 $k$ 枚举子集,则内层变成了能贴板子的情况,复杂度 $O(nk2^k\log m)$,保守估计有前 $20$ 个点,也就是 $80$ 分。
注意到 $n$ 小得不太正常。于是注意到先不考虑 $k$ 个额外点跑最小生成树然后再套上面的做法可以降到 $O(nk2^k\log n)$,常数减半。
此时除了把 $\log n$ 变成 $\alpha(n)$(排序常数很小其实可以不计的)外唯一的优化空间在 $k2^k$ 上。发现对于一种情况可以每加入一个新点跑一遍从而减少重复计算,上述优化全安上去是 $O(n2^k\alpha(n))$ 的,差不多就过了。
---
并查集合并的正确姿势是:
```cpp
inline void merg(ll x,ll y){
fa[fnd(x)]=fa[y];
}
```
**不是**:
```cpp
inline void merg(ll x,ll y){
fa[x]=fa[y];
}
```
下面的这段会把 $x$ 的子树分裂出来合并到 $y$ 上。
然后我试图检查并查集是否写错,检查的方式是加了一行 `assert(fnd(q[j].u)==fnd(q[j].v));`。
废话 `q[j].u` 的子树都分裂出来合并上去了当然查不出来啊!!!
### C - P14363 [CSP-S 2025] 谐音替换 / replace
- 知识点:哈希、trie、二维数点。
其实 ACam 也可以做(且我考场上想出来了),但我整个字符串技能树就点了哈希,外加 ACam 超纲了,所以我们讨论比较正常的做法。
首先的首先,**由于 $\forall i,|s_{i,1}|=|s_{i,2}|$,所以 $|t_1|\neq|t_2|$ 时答案必然为 $0$**。
首先不要读错题,一共只准换一次。
然后开始瞪样例,注意到 `bc->de` 和 `xabcx->xadex` 的共同点都是 `bc->de`,容易发现其实可以选的二元组一定是不同处仅包含 `bc->de` 且 $s_{i,1}\subset t_1$ 的。
也就是说,若我们称两个字符串去掉两边相同部分后为交换的**本质**,例如 `xabcx->xadex` 的**本质**是 `bc->de`,则只可能是**本质**相同且 $s_{i,1}\subset t_1$ 的 $(s_{i,1},s_{i,2})$ 可选。
于是我们需要找“**本质**相同”和“$s_{i,1}\subset t_1$”两个条件。
前者容易想到将**本质**做哈希。
后者如果将前者筛出的字符串拎出来判断就完蛋了,复杂度是 $O(nq)$ 的。但是发现本题空间 2GB,联赛字符串算法还要大空间的只有可能是 trie,于是考虑对 $s$ 中的每种**本质**中**本质**前及**本质**后的部分建 trie,于是询问就变成查询两边 trie 上都是当前点(询问串**本质**前后的部分)的祖先有几个,把 trie 拍成 dfs 序就变二维数点了。
### D - P14364 [CSP-S 2025] 员工招聘 / employ
- 知识点:DP、推式子。
>计数题七字真言:爆搜、DP、推式子。
这句话仍然有效。于是直接可以考虑 DP。下设 $pre_i$ 表示 $c_j<i$ 的 $j$ 个数,$t_i$ 表示 $c_j=i$ 的 $j$ 个数。
设 $dp_{i,j,k}$ 表示前 $i$ 个人中有 $j$ 个没录上,$1\le l\le i$ 中有 $k$ 个 $c_l\le j$ 的,则考虑第 $i+1$ 天,若 $s_{i+1}=1$,讨论该天是否录用新的人:
- 如果录用,则在还没用掉的人里选一个就行,即 $n-pre_j>i-k$ 时有 $dp_{i,j,k}\to dp_{i+1,j,k}$。
- 如果不录用,则第二维的值要 $+1$,此时枚举 $l\in[0,t_j]$ 为 $i$ 及以前 $c=j+1$ 的人数,有方程:
$$dp_{i,j,k}\times(pre_j-k)\times\text{C}_{t_{j+1}}^l\times\text{C}_{i-k}^l\times l!\to dp_{i+1,j+1,k+l+1}$$
其中 $\times(pre_j-k)$ 即从第 $i+1$ 天会没耐心的人中选一个,$\times\text{C}_{t_{j+1}}^l$ 即选出 $l$ 个 $c=j+1$ 的人,$\times\text{C}_{i-k}^l$ 选出这 $l$ 个人在前 $i$ 个人里的位置,最后 $\times l!$ 计算他们的排列顺序。
类似的,对于 $s_{i+1}=0$ 的情况,有方程:
$$dp_{i,j,k}\times(pre_{j+1}-k-l)\times\text{C}_{t_{j+1}}^l\times\text{C}_{i-k}^l\times l!\to dp_{i+1,j+1,k+l+1}$$
此时对于被毙掉的选手恰好是 $c=j+1$ 的情况额外判一下即可。
看上去是 $O(n^4)$ 的,但实际上受制于 $\sum t_j=n$,内三层只有 $O(n^2)$,总复杂度为 $O(n^3)$。
## NOIP 2025
菜,就要多练。
其实大家讲得已经很不错了,这里补上去纯粹是因为缺一块有点难看(?)。
### A - P14635 [NOIP2025] 糖果店 / candy(官方数据)
注意到 $m$ 特别大,容易想到会大量买 $x_i+y_i$ 最小的情况。
从此出发发现一种糖买两个的话这样显然是最便宜的,但可能出现其他糖买一个更便宜的情况。于是我们想到先买这些单个便宜的,再成对买 $x_i+y_i$ 最小的,此时最多还能买一个(因为能买两个刚才就买完了),能买就买一下。
然后发现样例 $6$ 少了 $1$。
然后发现其实单买的时候少买一个可能就能多买一对。由于单买的每两个平均性价比都不低于成对买的,所以最多只需要反悔最后一个。
小细节:注意判掉买单个的时候钱就花完了的情况。
复杂度 $O(n\log n)$,瓶颈在排序。
### B - P14636 [NOIP2025] 清仓甩卖 / sale(官方数据)
火药味已经上来了。感觉严格难于 employ。场上 $n^3$ 拼炸了。
首先 B 性质给了一个很强的提示。在性质中任何 $w=2$ 的排序都在 $w=1$ 的之后,所以唯一一种不合法的可能,就是我最后剩下 $1$ 块钱,但把最便宜的 $w=1$ 的换成没买的最贵的 $w=2$ 的会更优。
而有无 B 性质的差别就是没有性质 B 的时候 $w=2$ 后面还可能有 $w=1$,这时剩下的那一块钱会买到这段 $w=2$ 后的那个 $w=1$,此时要求的就是两个 $w=1$ 的原价和小于 $w=2$ 的那个。于是我们找到了不合法的情况的特征。这里为了方便,如果剩一块钱的时候后面没有 $w=1$ 了(即上面 B 性质中的情况)则第二个 $w=1$ 的原价视为 $0$。
所以不难想到的是设两个 $w=1$ 分别是 $i,j$,$w=2$ 的是 $k$,将**原价升序**排序(注意一下以防后面没法理解式子)后直接枚举 $i<j<k$,此时我们要求在 $j$ 之后的所有物品总共花 $m-2$ 块钱,其中 $k$ 花两块钱,所以这里方案数是 $\text{C}_{n-j}^{m-(n-j)-1}$。然后 $i$ 之前的价格是任意的所以再乘 $2^{i-1}$。
加上最后一块钱浪费掉的情况(也是 $\text{C}_{n-j}^{m-(n-j)-1}$ 种),一个 $n^3$ 的做法就完成了。
考虑优化。我们发现如果 $j,k$ 定下来那么合法的 $i$ 一定是一段前缀。那就是对着各段前缀求一个和,然后把 $\text{C}_{n-j}^{m-(n-j)-1}$ 提出来,即设前缀为 $[1,I]$ 则这组 $j,k$ 为 $2^{I}\text{C}_{n-j}^{m-(n-j)-1}$。
但我们还需要求 $I$ 的值。
好消息是对于同一个 $k$,当 $j$ 增大即我们买的另一个商品原价变大时,满足 $a_i+a_j<a_k$ 的 $a_i$ 的范围显然会变小(这就是为什么我们刚才没按性价比排序),于是 $j$ 整个扫过来 $I$ 就只要移动 $n$ 格。然后按上面式子算出答案就可以 $O(n^2)$ 解决了。
### C - P14637 [NOIP2025] 树的价值 / tree(官方数据)
- 抄了云斗的、LCA 的题解。后者主要是在正解状态那个地方不是很明确,所以建议直接看前者(或者我的,反正一样)。
---
首先每个数是贡献到其自身到根的路径上的,所以显然不能祖孙填相同的数。进一步的,不会有祖先比子孙的数小。
然后硬做的方案是每个点设置成子树内 $\text{mex}$。但手玩发现这样容易被做局,所以我们需要拿出一些点来给上面做贡献。我们定义它们为白点,给自己做贡献的是黑点。于是白点贡献的就是其祖先中的第一个黑点。
做到这里有暴力 DP:设 $dp_{u,i,j}$ 为 $u$ 子树内 $\text{mex}=i$ 且留了 $j$ 个白点的最大答案。合并儿子直接按照状态定义即将 $dp_{v_1,i_1,j_1}$ 与 $dp_{v_2,i_2,j_2}$ 合并到 $dp_{u,max\{i_1,i_2\},j_1+j_2}$。
然后从后往前递推,从 $dp_{u,i,j}$ 转移到 $dp_{u,i+1,j-1}$ 来完成消耗白点并提升 $u$ 的 $\text{mex}$ 的情况。
然后参考上面的转移过程我们会发现一个更加惊为天人的性质:每个黑点 $\text{mex}$ 最大的儿子必然是黑的!我们定义其为“重儿子”,则题目变成了一个类似于重链剖分的东西。而根据刚才的贡献原则,每个点的贡献则是从它到根之间最长重链的长度。
于是我们将这个长度丢到状态上维护起来,设 $dp_{u,i}$ 为**链顶** $u$ 到根最长重链长度为 $i$ 的答案。转移时枚举链的底端,贡献就是从链上点的轻儿子贡献过来。由于第二维是最长重链的长度所以可以每层开线段树进行维护来实现 $1\log$ 的转移,外加状态数只有重链所以是 $nm$,相乘得到复杂度就是 $O(nm\log n)$ 了。
### D - P14638 [NOIP2025] 序列询问 / query(官方数据)
这里讲倍增分块,私以为这是最好理解的。
首先 $L=R$ 时此题为滑动窗口板子。但 $L\neq R$ 时不能再对着每个区间维护了,但首先我们发现可以滑动窗口求出以某个点为右端点的极好区间的最大值。尽管区间个数是 $O(n)$ 了,但我们不可能只考虑这些区间,因为无法保证贡献给每个点的区间都一定是其右端点可能取到的最值。
考虑在二维平面上刻画问题,用点的横纵坐标表示区间的左右端点。则点 $i$ 的答案就是同时满足 $l\le i\le r$ 和 $L\le r-l+1\le R$ 的点集,即图中黄色区域和蓝色区域的交叠部分(红色区域)。

而我们刚才那个东西求出来的是一个平行四边形(下图中黄色、蓝色的部分分别可以求出):
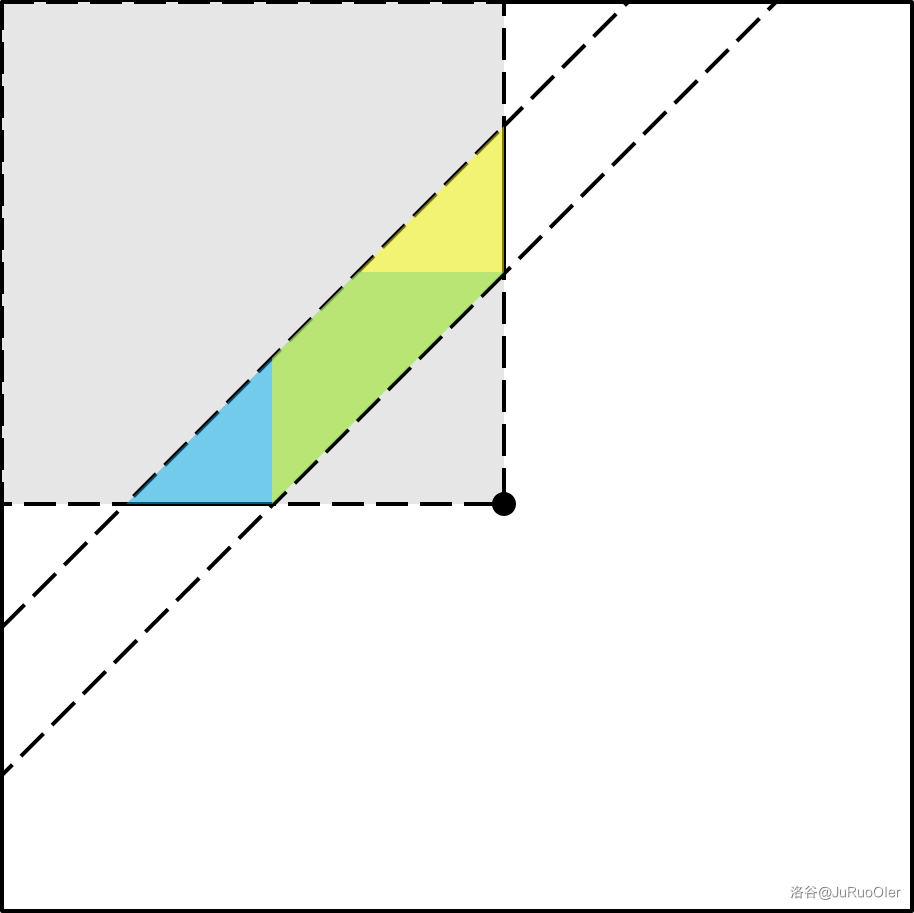
最值是允许重叠的,所以其实把两个平行四边形分别求一遍,也就是把以每个点为左端点和以每个点为右端点分别单调队列一次,就做完了。时间复杂度 $O(nq)$。
……吗?
在 $2L<R$ 的时候,图就变成这样了:
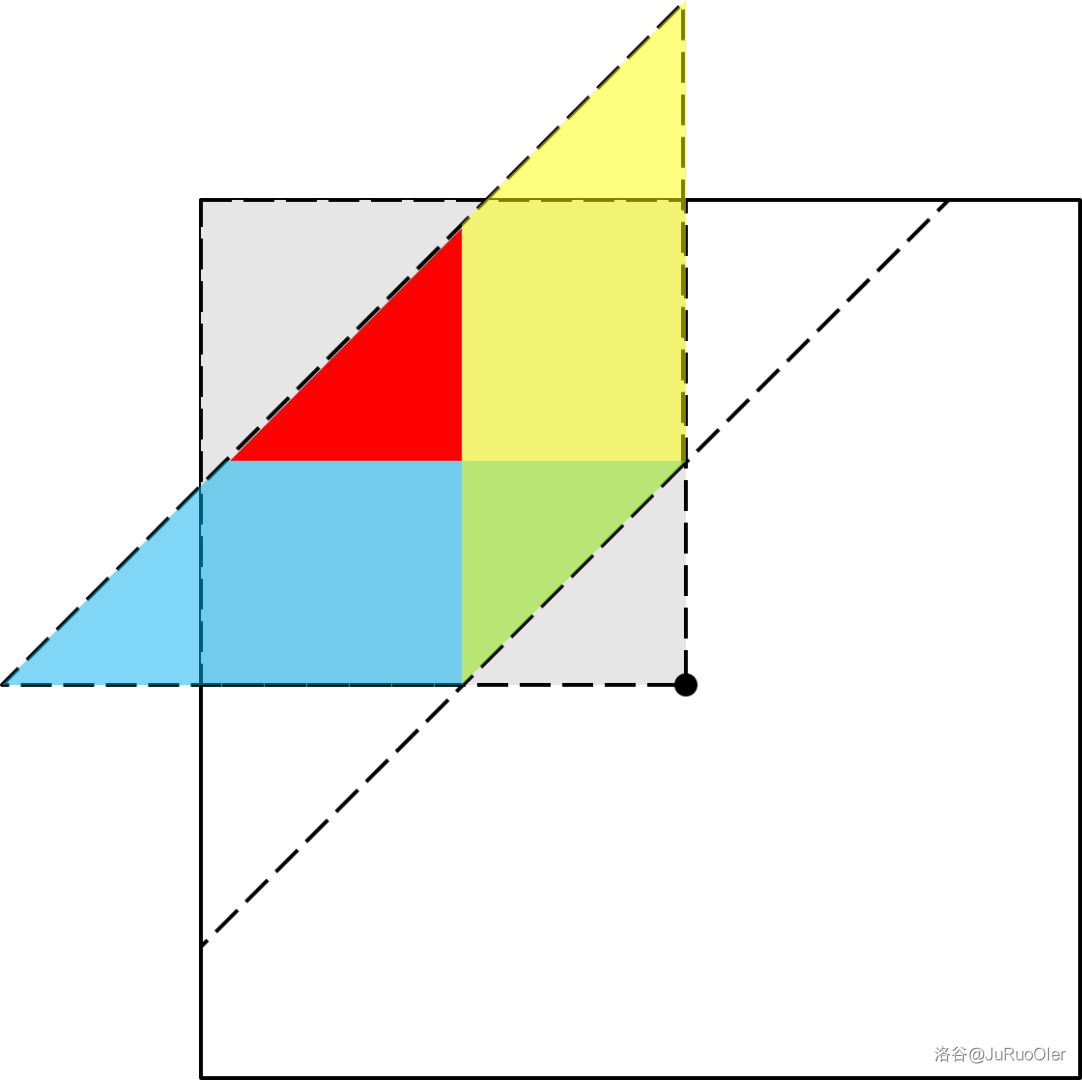
你会发现红色的三角形没算。
按刚才的方法递归地算下去固然没错,但复杂度会带 $\log$,所以需要优化。
考虑倍增分块,将长度范围分成若干块,第 $i$ 块是 $[2^i,2^{i+1}-1]$,则一共只会分成 $\log n$ 块。但这并不能改善复杂度。
但我们可以预处理每个“块区间”,即每段连续的块中每个位置的答案。这时,原询问区间 $[L,R]$ 就被“大卸三块”:设 $[l,r]$ 为其内最长的“块区间”,则答案必然在 $[L,l-1],[l,r],[r+1,R]$ 三段中,取个最值即可。
复杂度 $O(nq+n\log^2 n)$。
# 视频题解
由于技术问题(插入视频不正常,~~不知道是我的锅还是洛谷的锅~~实锤了就是洛谷的,所有视频全炸了,管理员赶紧修!),你可以直接去 B 栈搜 @[JuRuoOIer](https://space.bilibili.com/1366152279) 或者比赛名、题号等应该也能搜到。
~~不过我相信你不会想看的,毕竟讲得一坨。~~