10598
myee
·
·
题解
前言
发现洛谷把 bzoj 题给搬了过来,所以我把当时写的题解传过来了。
其实就一缝合题,没啥意思。
第一问
考虑对补图跑二分图带权最大独立集。
这一部分可以通过一个人类智慧的网络最大流实现。
0 -> 1 - n 101
1 - n -> n+1 - 2n inf, 当且仅当补图上有该边时连边
n+1 - 2n -> 2n+1 100
跑从源点 S=0 到汇点 T=2n+1 的最大流,即最小割。
然后就可以计算出男生、女生人数了。
如下图是样例。
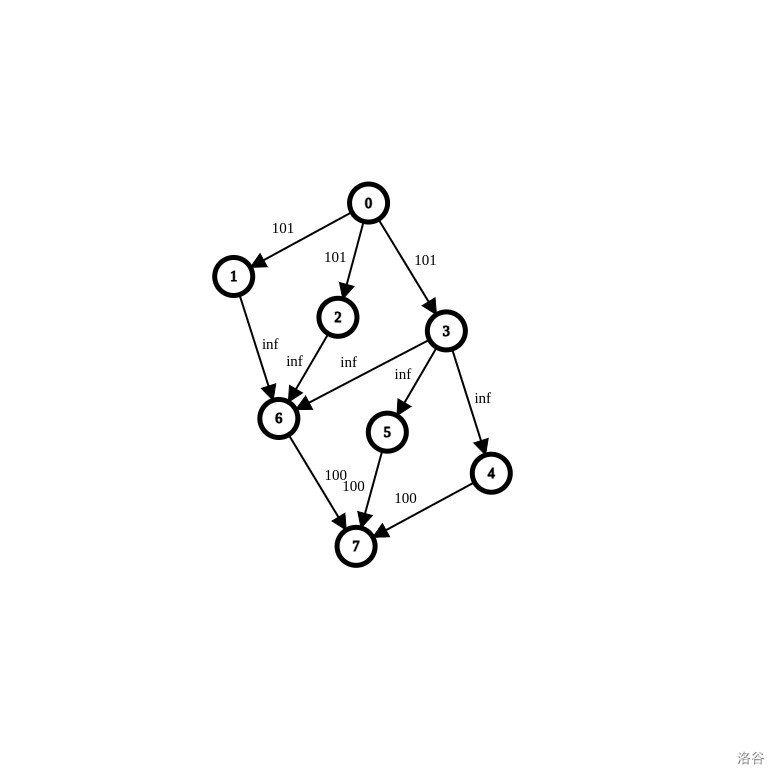
---
### 第二问
记 $n$ 个男生,$m$ 个女生的该图中任意挑 $k$ 条边的方案数为 $f_{n,m}=\binom{nm}{k}$,其中符合题目条件的选法有 $g_{n,m}$ 种。
则显然有
$$
f_{n,m}=\sum_{a,b}\binom na\binom mbg_{a,b}
$$
由**二维二项式反演**,我们得到
$$
g_{n,m}=\sum_{a,b}\binom na\binom mb(-1)^{n+m-a-b}f_{a,b}
$$
即答案为
$$
\sum_{a,b}\binom na\binom mb\binom{ab}k(-1)^{n+m-a-b}
$$
直接做就好了。
---
### Code
码头去掉了。
```cpp
Dinic D;
bol E[55][55];
modint C[5005][5005];
int main()
{
#ifdef MYEE
freopen("QAQ.in","r",stdin);
#endif
uint n,k,m;
scanf("%u%u%u",&n,&k,&m);
D.build((n+1)<<1);
for(uint i=1;i<=n;i++)D.insert(0,i,101),D.insert(i+n,n<<1|1,100);
for(uint i=1;i<=n;i++)for(uint j=1;j<=n;j++)E[i][j]=true;
while(m--){uint u,v;scanf("%u%u",&u,&v),E[u][v]=false;}
for(uint i=1;i<=n;i++)for(uint j=1;j<=n;j++)if(E[i][j])D.insert(i,j+n,-1);
ullt w=201llu*n-D.run(0,n<<1|1);
uint a=w%100;
uint b=w/100-a;
printf("%u %u\n",a,b);
AnyMod::ChgMod(19921228);
C[0][0]=1;
for(uint i=1;i<=5000;C[i][0]=1,i++)for(uint j=1;j<=i;j++)C[i][j]=C[i-1][j-1]+C[i-1][j];
modint ans;
for(uint i=0;i<=a;i++)for(uint j=0;j<=b;j++)
((i^j)&1)?ans-=C[a][i]*C[b][j]*C[(a-i)*(b-j)][k]:ans+=C[a][i]*C[b][j]*C[(a-i)*(b-j)][k];
ans.println();
return 0;
}
```