ABC144D 题解
FurippuWRY
·
·
题解
题意如下
其中 a 是底边长,b 是容器的高,x 是水的体积。
现在要把它倾斜,有三种情况。
图 1
图 2
图 3
前置知识
做这题你首先要知道三角函数、反三角函数、弧度制等知识。
三角函数中常用的有正弦函数、余弦函数、正切函数等。本题只用正切函数就可以 AC,正切函数的定义如下:
三角函数还有一个在平面直角坐标系里的定义,在这里不讲。
那么什么是反三角函数?反三角函数是三角函数的反函数。
反函数即定义域(函数自变量的取值范围)和值域(函数因变量的集合,即 y 值的集合)互换的函数。
我们利用反三角函数来求出一个三角函数值对应的角的大小。
要表示一个三角函数的反函数,用 \operatorname{arc}+ 函数名或在三角函数与自变量中间加上上标“-1”即可。
如正切函数,用 \arctan a 或 \tan^{-1}a 来表示反正切函数(a 是一个常数)。
在 C++ 的 cmath 库里,有一个函数 atan(),可以用它来计算一个数的反正切函数,结果是一个弧度数,(弧度制是表示角的大小的方法之一)但输出结果要求是角度,这时我们就要把弧度转换为角度。
角度与弧度的换算如下(\operatorname{rad} 为弧度单位):
也就是说,要把弧度数转换为角度,只要把这个弧度数乘 \dfrac{180}{\pi} 即可。
回归正题
先定义几个要用的变量:
容积 v=a^2b;
角度 ang;
$h=$ 图 2、图 3 中的 $CP$。
------------
先看第一种情况.。
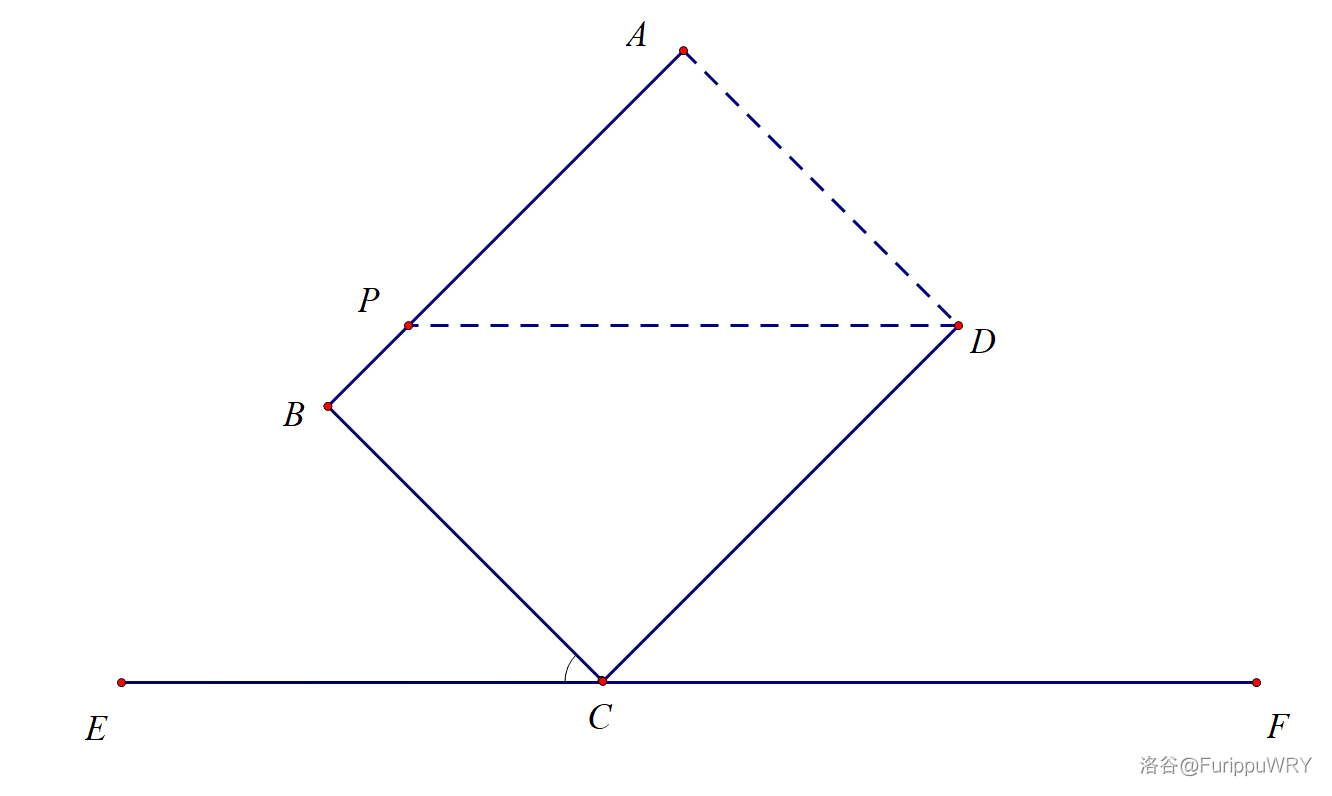
这种情况下,$x>\dfrac{v}{2}$,$PD\parallel EF$,$BC\parallel AD$。
由“两直线平行,同位角相等”可得 $\angle BCE=\angle ADP$。
也就是说,$\tan\angle BCE=\tan\angle ADP=\dfrac{AP}{AD}=\dfrac{m}{a}$。
我们只要求出 $\arctan \dfrac{m}{a}$ 再转换为角度即可。
求 $m$,可以先把剩余体积(即 $v-x$)乘 $2$,当作一个正方体,因为正方体的体积为边长的三次方,所以将剩余体积除容器底面积($a^2$)就可得到 $m$。
即 $m=\dfrac {2(v-x)}{a^2}$。
因为这个容器是个长方体,所以 $AD=BC=a$,所以 $\arctan \dfrac{m}{a}=\arctan \dfrac{2(v-x)}{a^3}$,$ang=\dfrac{180}{\pi}\times\arctan \dfrac{2(v-x)}{a^3}$。
------------
第二、三种情况。
由于这两种情况本质上是一样的,所以放在一起讲。
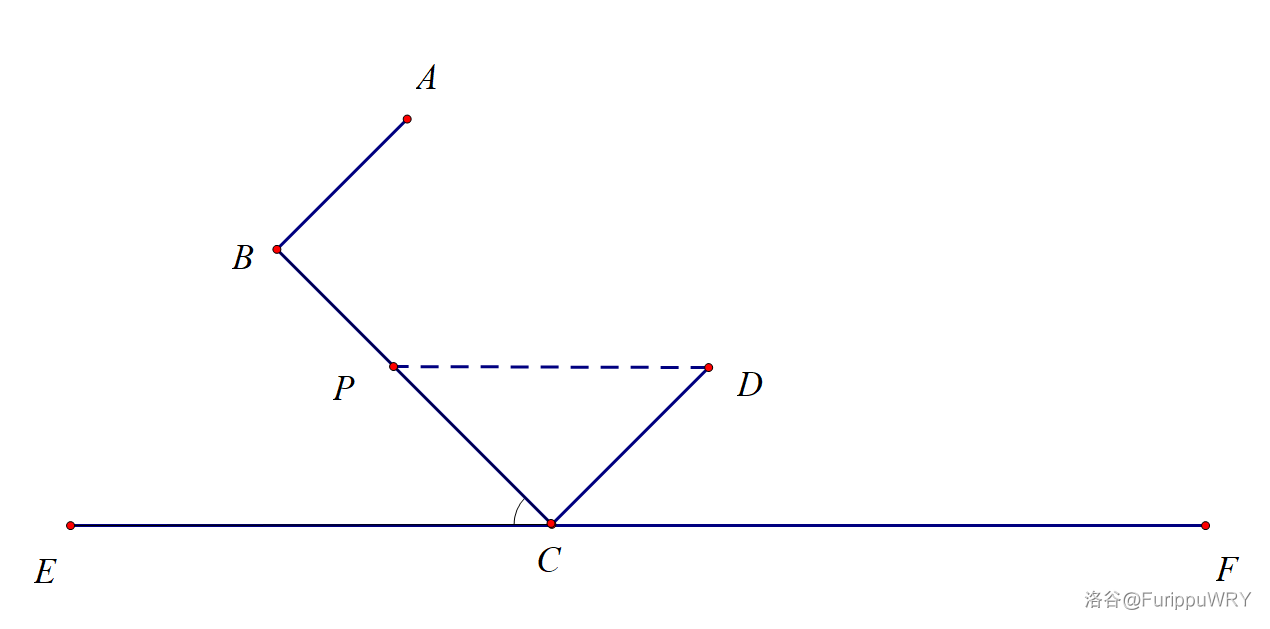
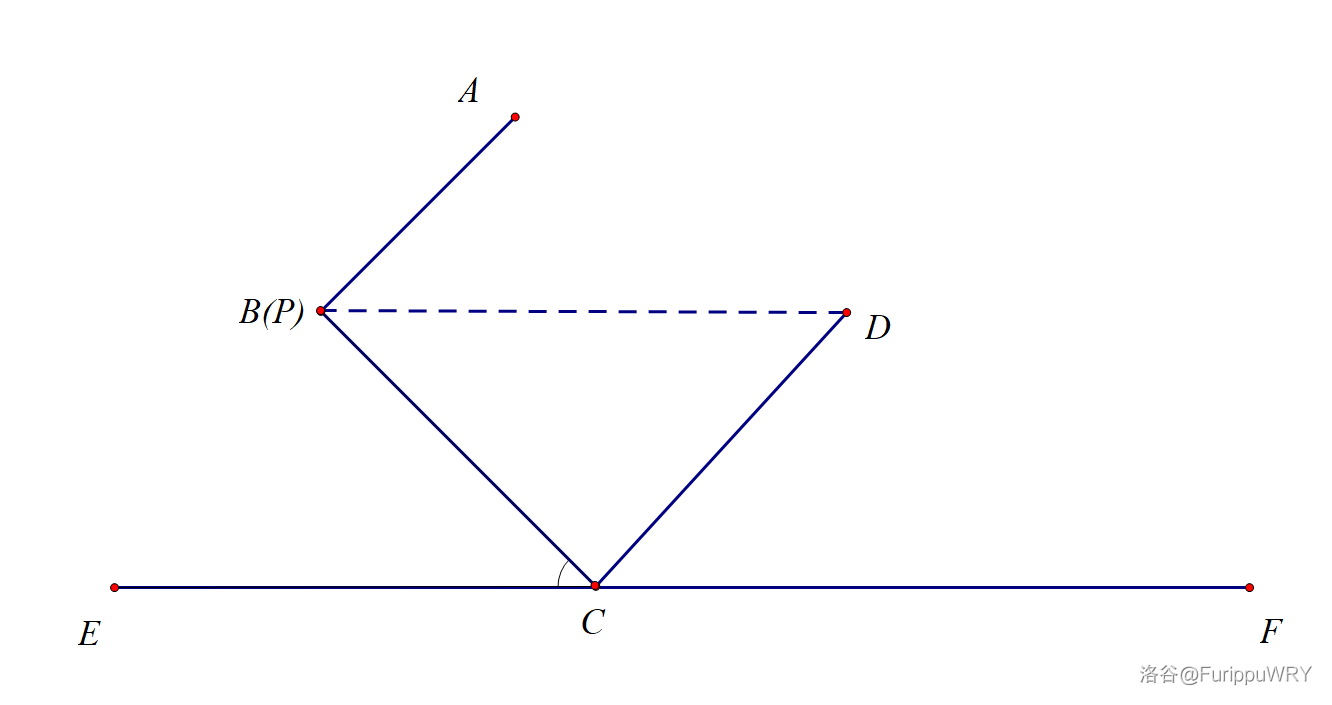
这种情况下,$x\le\dfrac{v}{2}$。
这里要求出 $\tan \angle BCE$ 和第一种情况类似,$PD\parallel EF$,由“两直线平行,内错角相等”可得 $\angle BCE=\angle DPC$。
即 $\tan\angle BCE=\tan\angle DPC=\dfrac{DC}{PC}=\dfrac{b}{h}$。
求 $h$,先求 $2x$,得到一个长方体。
长方体的体积 $=$ 长 $\times$ 宽 $\times$ 高,这里的高就是 $h$,所以长 $\times$ 宽 $=ab$,即 $h=\dfrac{2x}{ab}$。
所以 $\arctan\dfrac{b}{h}=\arctan\dfrac{ab^2}{2x}$,$ang=\dfrac{180}{\pi}\times\arctan\dfrac{ab^2}{2x}$。
综上所述,
$$ang=\begin{cases}\dfrac{180}{\pi}\times\arctan \dfrac{2(v-x)}{a^3},x>\dfrac{v}{2}\\\dfrac{180}{\pi}\times\arctan\dfrac{ab^2}{2x},x\le\dfrac{v}{2}\end{cases}$$
------------
# AC code
```cpp
#include <bits/stdc++.h>
using namespace std;
double a, b, x, ang, v, m, h; //ang 为角度,v 为容积,m 为 AP,h 为 CP
const double pi = 3.14159265358979;
int main() {
cin >> a >> b >> x;
v = a * a * b;
if (x > v / 2){//第一种情况
m = (v - x) * 2 / (a * a);
ang = atan(m / a) * (180 / pi);//求出反正切函数的值,弧度化为角度
}
else {//第二、三种情况
h = 2 * x / b / a;
ang = atan(b / h) * (180 / pi);
}
printf("%.10lf",ang);//要输出 10 位小数
return 0;
}
```
#### 化简:
```cpp
#include <bits/stdc++.h>
using namespace std;
double a, b, x, v, pi = 3.14159265358979;
int main() {
cin >> a >> b >> x;
v = a * a * b;
if (x > v / 2) {
printf("%.10lf", atan((v - x) * 2 / (a * a * a)) * (180 / pi));
}
else {
printf("%.10lf",atan(a * b * b / 2 / x) * (180 / pi));
}
return 0;
}
```