题解 P5031 【庞氏骗局】
天南月
·
·
题解
Markdown炸了,已update
题目简述
有K1份1万元和K2份2万元。每一天都可以选择两份钱,各消费1万元。每天选择的两份钱不能与之前重复。求花光所有的钱,共有多少不同的方案集合。
方案没有先后顺序,每一天不分先后。
例如:如果第一天选择了(1,2)两份钱,第二天就不能花(1,2),但可以从(2,3)或(1,3)这样的组合中拿钱。
输入格式
一行,两个整数,K1,K2
输出格式
一行,一个整数,表示方案数
样例:
输入 2 2
输出 2
做法(以下图中加粗的为新点)
如果有什么问题可以私信或者评论,如果我到时候还没退役会尽量回答的
可以将原题目转化成:
在一张无向图上有K1个出度为一,K2个出度为2的点,每个点的标号都不一样,求图的总可能方案数。
容易发现,最后一定是由若干个环和若干条链组成的图,像这样:
每一条链的两端都是出度为一的点,易得若图有方案,则出度为一的点个数必为偶数。
我们先考虑特殊情况。
当K2=0时,易得方案数为(K1-1)*(K1-3)*(K1-5)……
将该方案数记为sum1
当K1=0时,考虑DP。记f_{i\ j}为i个点组成j个环的方案数,则有f_{i\ j}=f_{i-1\ j}*(i-1)+f_{i-3\ j-1}*C^2_{i-1}
那么K2的总方案数就是\sum^{K2 \over 3}_{i=1}f_{K2 \ i}
DP边界是f_{0\ 0}=1。
接下来我们解释上面的DP式子。
* 1.把第$i$个点插入已有的j个环中,可由$f_{i-1\ j}$转移而来。如图:
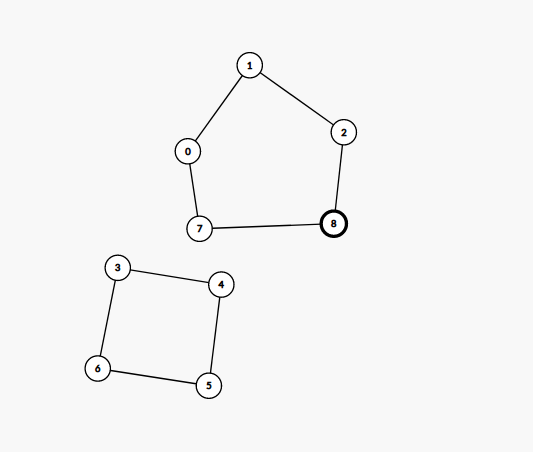会重复,故该情况的方案数为$f_{i-1\ j}*(i-1)
- 2.从已有的i-1个点中选出2个点与点i组成一个新的环,剩下的i-3点再组成j-1个环的方案数,故该情况的方案数为f_{i-3\ j-1}*C^2_{i-2}。至于为什么新环的大小为3,因为环最小为3,如果新环更大,就相当于点i插入一个环中,与之前的情况重复。如图:
特殊情况考虑完了,接下来把两种情况综合到一起。我们发现,其实总方案数就是
而将$i$个点放入$j$条长度为2的链中的方案数为
$j*(j+1)*(j+2)*……*(j+i-1)={(j+i-1)! \over (j-1)!}
即将第1个点放入有j个空可以放,故有j种方案;将第2个点放入有j+1个空可以放,故有j+1种方案……以此类推。
贴代码:
```cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1e9+7,N=6e3;
int k1,k2;
int sum1,zs1;
int f[N][2005];
int jc[N<<1],inv[N<<1];
int QP(int x,int k){
int ret=1;
while(k){
if(k&1)ret=ret*x%mod;
k>>=1;
x=x*x%mod;
}
return ret;
}
signed main(){
scanf("%lld%lld",&k1,&k2);
if(k1&1){puts("0");return 0;}
zs1=k1>>1;
sum1=1;
for(int i=k1-1;i>=0;i-=2)sum1=(sum1*i)%mod;
jc[0]=1;
f[0][0]=1;
for(int i=1;i<=k2+zs1;++i)jc[i]=jc[i-1]*i%mod;
inv[k2+zs1]=QP(jc[k2+zs1],mod-2);
for(int i=k2+zs1-1;i>=0;--i)inv[i]=inv[i+1]*(i+1)%mod;
for(int i=2;i<=k2;++i){
int x=((i-1)*(i-2)>>1)%mod;
for(int j=1;j<=i/3;++j){
f[i][j]=f[i-1][j]*(i-1)%mod;
(f[i][j]+=(f[i-3][j-1]*x)%mod)%=mod;
}
}
for(int i=3;i<=k2;++i)
for(int j=1;j<=i/3;++j)
(f[i][0]+=f[i][j])%=mod;
int ans=0;
if(!k2)ans=sum1;
else if(!k1)ans=f[k2][0];
else{
int ret=0,cs=inv[zs1-1]*jc[k2]%mod;
for(int i=0;i<=k2;++i){
ret=inv[i]*inv[k2-i]%mod*jc[zs1+i-1]%mod*f[k2-i][0]%mod;
(ans+=ret)%=mod;
}
(ans*=sum1*cs%mod)%=mod;
}
printf("%lld",ans);
return 0;
}
```