P6955 [NEERC2017] Designing the Toy 题解
scp020
·
2023-08-10 22:37:24
·
题解
spj 提供者写的题解。
[NEERC2017] Designing the Toy
小清新构造题,需要一点空间想象能力。
值得注意的是每个单位正方体是可以悬空的。
解法
题目大意是给定一个空间几何体(可以不紧挨着)的三视图中可以看到的单位正方体的数量 a,b,c ,让你构造出这个空间几何体。
首先考虑无解情况,如果 a,b,c 中最大值大于其余两个数的乘积,则无解。因为考虑有遮挡关系时我们可以尽可能多放正方体,而一个面可以看到 a 个正方体(下面不妨设 a 最小,c 最大),另一个面可以看到 b 个正方体,则最多可以放 a \times b 个正方体,即一个 1 \times a \times b 的空间几何体。
再考虑有解的情况。下面拿样例举例,考虑贴着 c 所代表的平面放正方体。
首先要满足 a 所代表的平面的要求,沿着对角线放,如图所示。
放完后我们考虑利用遮挡关系,在不影响 a 的情况下放 b ,即可以在这个对角线的左侧放 b-a 个正方体,如图所示。
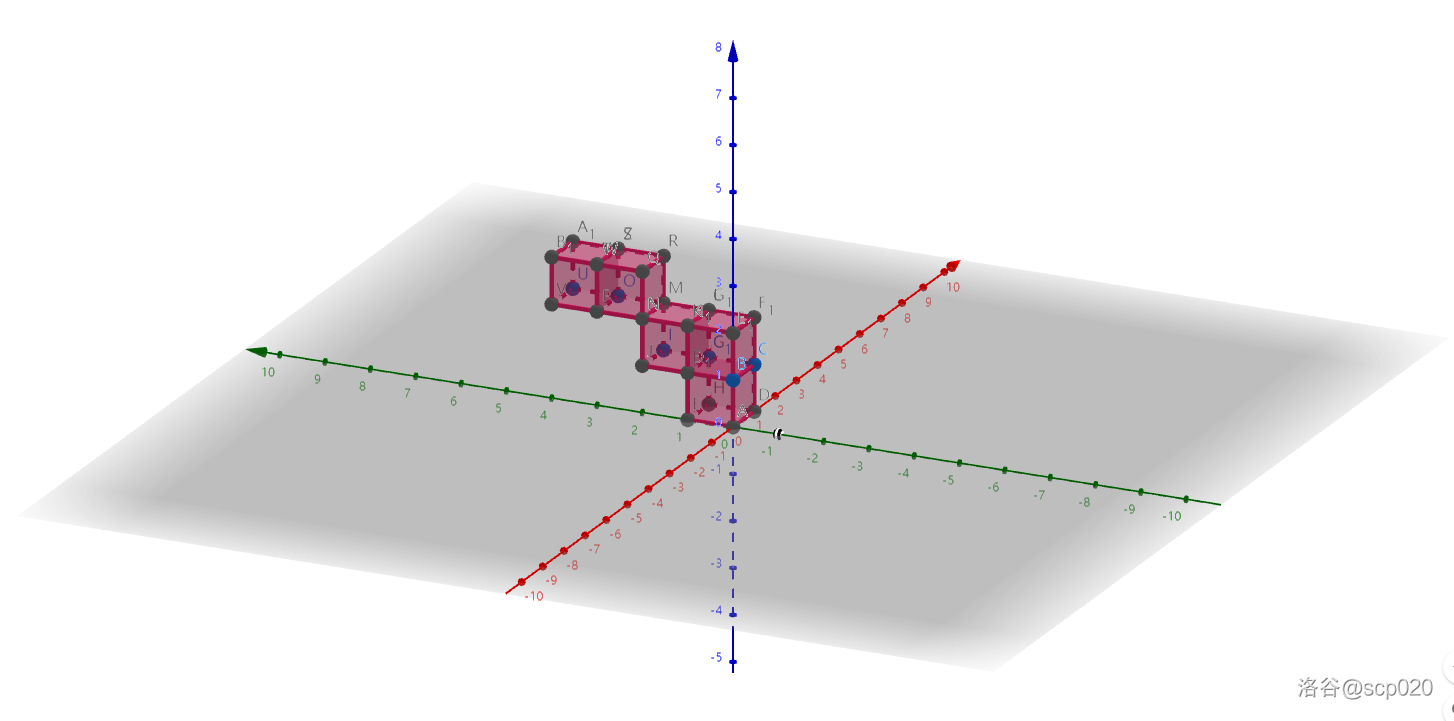
### 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
#define Putchar(c) p3==p4 and (fwrite(Ouf,1,1<<21,stdout),p3=Ouf),*p3++=c
char Ouf[1<<21],*p3=Ouf,*p4=Ouf+(1<<21);
inline void write(int x)
{
if(x<0) Putchar('-'),x=-x;
if(x>=10) write(x/10),x%=10;
Putchar(x^48);
}
int a,b,c,vis[200][200],cnt,v[200][4];
pair<int,int> p[4];
int main()
{
cin>>p[1].first>>p[2].first>>p[3].first,p[1].second=1,p[2].second=2,p[3].second=3,sort(p+1,p+4);
a=p[1].first,b=p[2].first,c=p[3].first;
if(a*b<c)
{
cout<<-1;
return 0;
}
for(int i=1;i<=a;i++) v[++cnt][p[1].second]=i,v[cnt][p[2].second]=i,v[cnt][p[3].second]=1,vis[i][i]=1;
for(int i=a+1;i<=b;i++) v[++cnt][p[1].second]=i,v[cnt][p[2].second]=a,v[cnt][p[3].second]=1,vis[i][a]=1;
for(int i=1;i<=b;i++)
for(int j=1;j<=a && cnt<c;j++) if(!vis[i][j]) v[++cnt][p[1].second]=i,v[cnt][p[2].second]=j,v[cnt][p[3].second]=1;
write(cnt),Putchar('\n');
for(int i=1;i<=cnt;i++,Putchar('\n')) for(int j=3;j;j--) write(v[i][j]),Putchar(' ');
fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);
return 0;
}
```