2.1.0 组合数学基本
LTTXiaochuan
·
·
算法·理论
系列说明:此为笔者的笔记库中的某一篇,其中所指代的章节并不一定被笔者上传投稿了。希望本系列的发布能给部分读者带来一定帮助。
2.1.0 组合数学基本
嗯,终于来了。伟大无需多言。
Part.0 二项式定理 & 杨辉三角
我觉得还是先说组合数怎么算比较好。
示例代码:(用来计算 \operatorname{C}^b_a)
const int N=114514,mod=1919810;
int fact[N],ifact[N],inv[N];
int qmi(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
void init()
{
inv[1]=1;
fact[0]=ifact[0]=1;
for(int i=1; i<N; i++)
{
fact[i]=1LL*fact[i-1]*i%mod;
if(i!=1) inv[i]=1LL*(mod-mod/i)*inv[mod%i]%mod;
ifact[i]=1LL*ifact[i-1]*inv[i]%mod;
//下面是非递推逆元求法,有概率T飞
// fact[i]=1LL*fact[i-1]*i%mod;
// ifact[i]=1LL*ifact[i-1]*qmi(i,MOD-2)%mod;
}
}
int C(int a,int b)
{
return 1LL*fact[a]*ifact[a-b]%mod*ifact[b]%mod; //千万不要漏了"1LL"
}
当然,如果你喜欢,且数据范围比较小,还可以使用递推法求组合数:
\binom{n}{m}=\binom{n-1}{m-1}+\binom{n-1}{m}
void init()
{
C[0][0]=0,C[1][0]=C[1][1]=1;
for(int i=2; i<N; i++)
{
C[i][0]=1;
for(int j=1; j<=i; j++)
C[i][j]=(C[i-1][j]+C[i-1][j-1])%k;
}
}
然后我们再来说说二项式定理。
二项式定理:
(a+b)^n=\binom{n}{0}a^nb^0+\binom{n}{1}a^{n-1}b^1+...+\binom{n}{k}a^{n-k}b^k+...\binom{n}{n}a^0b^n
写成好看一些的求和式:
(a+b)^n=\sum_{i=0}^n \operatorname{C}_n^i a^{n-i}b^i
这里甚至有一道板子:P1313 [NOIP 2011 提高组] 计算系数 - 洛谷
代码我就不放了。
朱世杰恒等式
原式是这样的:
\sum_{i=0}^m\binom{n+i}{i}=\binom{n+m+1}{m}
这等价于
\sum_{i=n}^m \binom in=\binom{m+1}{n+1}
Part.1 卢卡斯定理
上面的组合数求法有一处较为严重的问题:
于是我们掏出组数大定理——卢卡斯定理。
---
**卢卡斯定理**:令 $p$ 为一个质数,令 $n$ 和 $m$ 为非负整数。设 $n$ 和 $m$ 的 $p$ 进制表示分别为:
$$
n = n_k p^k + \dots + n_1 p + n_0 \\
m = m_k p^k + \dots + m_1 p + m_0
$$
其中 $0 \le n_i, m_i < p$。
那么,我们有以下的同余关系
$$
\binom{n}{m} \equiv \prod_{i=0}^{k} \binom{n_i}{m_i} \pmod{p}
$$
该定理的一个等价的、更常用于递归计算的形式是
$$
\binom{n}{m} \equiv \binom{\lfloor n/p \rfloor}{\lfloor m/p \rfloor} \binom{n \bmod p}{m \bmod p} \pmod p
$$
我们将证明这个递归形式,因为原定理可以由递归形式反复推导得出。
##### 【Proof】
证明的核心是利用多项式 $(1+x)^n$ 的二项式展开,并考虑其在模 $p$ 意义下的系数。
**引理:** 对于任意质数 $p$,我们有同余式
$$
(1+x)^p \equiv 1 + x^p \pmod p
$$
根据二项式定理,将 $(1+x)^p$ 展开
$$
(1+x)^p = \binom{p}{0}x^0 + \binom{p}{1}x^1 + \dots + \binom{p}{p-1}x^{p-1} + \binom{p}{p}x^p
$$
考察中间的系数 $\binom{p}{k}$,其中 $1 \le k \le p-1$。
$$
\binom{p}{k} = \frac{p!}{k!(p-k)!} = \frac{p \cdot (p-1)!}{k!(p-k)!}
$$
因为 $p$ 是质数,且 $1 \le k \le p-1$,所以分母 $k!$ 和 $(p-k)!$ 中没有任何因子是 $p$ 的倍数。这意味着 $k!$ 和 $(p-k)!$ 都与 $p$ 互质。
因此,在 $\binom{p}{k}$ 的表达式中,分子有一个因子 $p$,而分母没有。所以 $\binom{p}{k}$ 必然是 $p$ 的倍数。
即
$$
\binom{p}{k} \equiv 0 \pmod p \quad \text{for } 1 \le k \le p-1
$$
将这个结论代入展开式,所有中间项在模 $p$ 意义下都为 0
$$
(1+x)^p \equiv \binom{p}{0}x^0 + 0 \cdot x^1 + \dots + 0 \cdot x^{p-1} + \binom{p}{p}x^p \pmod p
$$
由于 $\binom{p}{0} = 1$ 和 $\binom{p}{p} = 1$,我们得到
$$
(1+x)^p \equiv 1 + x^p \pmod p
$$
证毕。
**卢卡斯定理:**
我们的目标是求 $\binom{n}{m} \pmod p$。显有 $\binom{n}{m}$ 是多项式 $(1+x)^n$ 中 $x^m$ 项的系数。
将 $n$ 写成 $p$ 进制的单步分解形式:$n = q_n p + r_n$,其中 $q_n = \lfloor n/p \rfloor$ 是商, $r_n = n \pmod p$ 是余数。
同样地,$m = q_m p + r_m$,其中 $q_m = \lfloor m/p \rfloor$,$r_m = m \pmod p$。
考虑多项式 $(1+x)^n \pmod p$:
$$
\begin{aligned}
(1+x)^n &= (1+x)^{q_n p + r_n} \\
&= (1+x)^{q_n p} \cdot (1+x)^{r_n} \\
&= \left((1+x)^p\right)^{q_n} \cdot (1+x)^{r_n}
\end{aligned}
$$
由引理得
$$
(1+x)^n \equiv (1+x^p)^{q_n} \cdot (1+x)^{r_n} \pmod p
$$
分别对右侧的两项进行二项式展开
$$
(1+x^p)^{q_n} = \sum_{i=0}^{q_n} \binom{q_n}{i} (x^p)^i = \sum_{i=0}^{q_n} \binom{q_n}{i} x^{ip} \\
(1+x)^{r_n} = \sum_{j=0}^{r_n} \binom{r_n}{j} x^j
$$
将它们相乘
$$
(1+x)^n \equiv \left( \sum_{i=0}^{q_n} \binom{q_n}{i} x^{ip} \right) \left( \sum_{j=0}^{r_n} \binom{r_n}{j} x^j \right) \pmod p
$$
考虑右侧乘积展开式中 $x^m$ 项的系数(即 $\binom{n}{m}$)。$x^m$ 项是由左边和式中的 $x^{ip}$ 项与右边和式中的 $x^j$ 项相乘得到的,其指数满足 $ip + j = m$。
又 $m = q_m p + r_m$,且 $0 \le r_n, r_m < p$,$0 \le j \le r_n < p$。
代入得
$$
ip + j = q_m p + r_m
$$
整理得
$$
(i - q_m)p = r_m - j
$$
由于 $0 \le j < p$ 且 $0 \le r_m < p$,所以 $-p < r_m - j < p$。
这意味着 $r_m - j$ 只有在等于 0 时才可能是 $p$ 的倍数。因此,这个方程有唯一解:
$$
r_m - j = 0 \implies j = r_m
$$
$$
i - q_m = 0 \implies i = q_m
$$
所以,要构成 $x^m$ 项,必须从第一个和式中选取 $i=q_m$ 的项,并从第二个和式中选取 $j=r_m$ 的项。
* 从 $\displaystyle \sum_{i=0}^{q_n} \binom{q_n}{i} x^{ip}$ 中选取的系数是 $\displaystyle \binom{q_n}{q_m}$。
* 从 $\displaystyle \sum_{j=0}^{r_n} \binom{r_n}{j} x^j$ 中选取的系数是 $\displaystyle \binom{r_n}{r_m}$。
因此,$(1+x)^n$ 中 $x^m$ 项的系数在模 $p$ 意义下等于这两项系数的乘积。
即
$$
\binom{n}{m} \equiv \binom{q_n}{q_m} \binom{r_n}{r_m} \pmod p
$$
将 $q_n, q_m, r_n, r_m$ 的定义代回,即
$$
\binom{n}{m} \equiv \binom{\lfloor n/p \rfloor}{\lfloor m/p \rfloor} \binom{n \bmod p}{m \bmod p} \pmod p
$$
证毕。
示例代码:[P3807 【模板】卢卡斯定理/Lucas 定理 - 洛谷](https://www.luogu.com.cn/problem/P3807)
```c++
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
int inv[N];
int fact[N],ifact[N];
int n,m,p;
void init()
{
inv[1]=1;
fact[0]=ifact[0]=1;
for(int i=1; i<N; i++)
{
fact[i]=fact[i-1]*i%p;
if(i>1) inv[i]=(p-p/i)*inv[p%i]%p;
ifact[i]=ifact[i-1]*inv[i]%p;
}
}
int C(int a,int b)
{
if(a<b) return 0;
return fact[a]*ifact[a-b]%p*ifact[b]%p;
}
int lucas(int a,int b) //写成函数其实就是这样
{
if(b==0) return 1;
return C(a%p,b%p)*lucas(a/p,b/p)%p;
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T;
cin>>T;
while(T--)
{
cin>>n>>m>>p;
init();
cout<<lucas(n+m,n)<<"\n";
}
return 0;
}
```
### Part.2 容斥原理
> 这玩意讲了跟没讲似的。
**德摩根律**:
$$
\overline{\bigcup_{i=1}^n A_i} = \bigcap_{i=1}^n \overline{A_i}
\\
\overline{\bigcap_{i=1}^n A_i} = \bigcup_{i=1}^n \overline{A_i}
$$
**容斥原理**:
$$
\left|\bigcup_{i=1}^n A_i\right| = \sum_{i=1}^n |A_i| - \sum_{1 \leq i < j \leq n} |A_i \cap A_j| + \sum_{1 \leq i < j < k \leq n} |A_i \cap A_j \cap A_k| - \cdots + (-1)^{n-1} \left|\bigcap_{i=1}^n A_i\right|
\\
\left|\bigcap_{i=1}^n \overline{A_i}\right| = |U| - \sum_{i=1}^n |A_i| + \sum_{1 \leq i < j \leq n} |A_i \cap A_j| - \sum_{1 \leq i < j < k \leq n} |A_i \cap A_j \cap A_k| + \cdots + (-1)^n \left|\bigcap_{i=1}^n A_i\right|
$$
**广义容斥原理**:
$$
N(r) = \sum_{k=r}^n (-1)^{k-r} \binom{k}{r} S_k
$$
其中 $S_k$ 的定义如下,表示至少具有 $k$ 个性质的元素集合(交集)。
$$
S_k = \sum_{1 \leq i_1 < i_2 < \cdots < i_k \leq n} |A_{i_1} \cap A_{i_2} \cap \cdots \cap A_{i_k}|
$$
关于广义容斥原理的推导,有比较通俗易懂的组合推导方法。下面我们就来讲解。
需要选出**恰好**具有 $r$ 种性质的元素的集合 $N(r)$,以 $r=2,n=4$ 为例,需要首先选出两两大集合相交得到的所有集合,也就是下图右两种形状的集合。这样两两相交的集合可以由这几种组合生成:$(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)$。当然,这部分其实是 $S_2$,我们并不关心具体的 $S_2$ 是怎么来的。重要的是,如何计算重叠部分的重叠次数。
先考虑恰好具有 $3$ 个性质的元素。例如,性质分别为 $A,B,C,D$,我们考虑恰好具有 $A,B,C$ 性质的元素个数。$S_2$ 此时未被去重,其中任意两个集合的交集都包含恰含三个性质的元素,但并不是所有交集都有恰含 $A,B,C$ 性质的元素。只有 $(1,2),(1,3),(2,3)$ 有这种元素。$S_3$ 统计的就是 $(A,B,C),(A,B,D),(A,C,D),(B,C,D)$ 这四种三性质元素的集合,每一种都如上被统计了 $3$ 遍。这里的“$3$”,其实是从 $3$ 个性质中选出 $2$ 个性质,即 $\binom{3}{2}$,并利用它们产生的交集。
其它种的同理,都是利用我们需要的集合(下图右,即最开始选出来的那些)产生出来额外的交集。比如 $4$ 个性质的,就相当于从 $4$ 个性质中任选 $2$ 个,每两个我们需要的集合就能产生一个重叠。于是,对于 $k$ 个性质的 $S_k$,单组性质产生的重叠数量就是 $\binom{k}{r}$ 了。希望下面的配图能帮助读者(笔者?)更好理解。
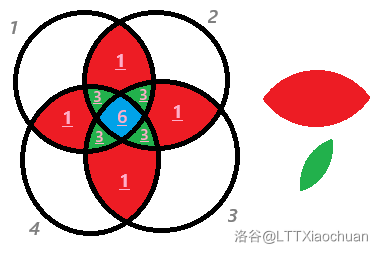
容斥原理的例题讲解请参见 2.1.x 的 **T5**。
### Part.3 经典组合模型
> 这个要是让某某来讲十天半个月都不一定讲得完。
##### #000 可重排列与组合
**模型定义**:可以重复取数的排列/组合。
假设从 $n$ 个数中取 $m$ 个。
**可重排列计算公式**:$n^m
可重组合计算公式:\binom{n+m-1}{m}
001 小球(不定方程)模型
模型定义:多元线性方程的解的数量问题。
已知线性方程 x_1+x_2+\cdots+x_n=m,求方程非负整数解的个数。
可以把问题转化为:“有 m 个小球放进 n 个盒子里,可以有空盒”。那么只需要把 n 个盒子变成 n-1 个隔板,混进小球里当做小球,然后再从这 n+m-1 个“小球”中选 m 个变回真正的小球(或者选 n-1 个变回隔板)即可。
计算公式:\binom{n+m-1}{m}
不难发现上式正好是可重组合数的计算公式。为什么呢?我们可以这样:可重组合数就是挑选重复元素。于是定义 x_i 为挑选了第 i 个元素 x_i 次,一共选了 m 个元素。所以公式是相同的。
由此我们还可以拓展出单调序列模型——给定序列长度 m 和取值范围 [1,n] 时,求解序列数量。不难发现可重组合数序列就是不减序列。如果要求严格单调,不难发现组合数序列就是严格单调序列。直接套上面的公式即可。注意是选几个就把谁放下面。要练习单调序列模型,读者可以尝试这道题:P6475 [NOI Online #2 入门组] 建设城市 - 洛谷,只要熟练运用刚才的知识就可以轻松顺利 AC。
002 球盒模型
下面的表格列出了所有的球盒问题的解法。
| 球 (k) |
盒子 (n) |
限制条件 |
解法/公式 |
备注 |
| 不同 |
不同 |
无限制 |
n^k |
每个球都有n种选择 |
| 不同 |
不同 |
每个盒最多1个 (k \le n) |
P(n, k) = \frac{n!}{(n-k)!} |
排列 |
| 不同 |
不同 |
每个盒至少1个 (k \ge n) |
n! \cdot S(k, n) |
第二类斯特林数乘以盒子的全排列 |
| 相同 |
不同 |
无限制 |
C(k+n-1, n-1) = \binom{k+n-1}{n-1} |
隔板法,允许空盒 |
| 相同 |
不同 |
每个盒最多1个 (k \le n) |
C(n, k) = \binom{n}{k} |
组合,选出k个盒子放球 |
| 相同 |
不同 |
每个盒至少1个 (k \ge n) |
C(k-1, n-1) = \binom{k-1}{n-1} |
隔板法,不允许空盒 |
| 不同 |
相同 |
无限制 |
\sum_{i=1}^{n} S(k, i) |
第二类斯特林数求和 |
| 不同 |
相同 |
每个盒最多1个 (k \le n) |
1 |
盒子相同,放法只有一种 |
| 不同 |
相同 |
每个盒至少1个 (k \ge n) |
S(k, n) |
第二类斯特林数 |
| 相同 |
相同 |
无限制 |
\sum_{i=1}^{n} p(k, i) |
整数拆分数求和 |
| 相同 |
相同 |
每个盒最多1个 (k \le n) |
1 |
盒子相同,放法只有一种 |
| 相同 |
相同 |
每个盒至少1个 (k \ge n) |
p(k, n) |
整数拆分数 |
注意到右侧备注中粗体标注的文本,这些问题对应的解法没有一个直接的单项式,而是需要通过一些复杂的递推或其它办法预先处理出某类数。其中最常见的就是第二类斯特林数。这个数列将会在 2.1.2 节单独说明。