题解 P5677 【[GZOI2017]配对统计】
harryzhr
·
·
题解
蒟蒻的第一篇题解
题目传送门 洛谷P5677 [GZOI2017]配对统计
前情提要
此题要用到树状数组,没有学过的朋友可以先去做做洛谷P3374 【模板】树状数组 1
简要题意
一组数 a_1,a_2,\cdots,a_n
一组配对 (x,y) 是好的配对(以后简称好对)当且仅当 (x,y) 使得 \left\vert a_x-a_y\right\vert 最小。
多组询问 [l,r] 中好对的个数。
思路
寻找所有好对
首先我们来理解题意:
所以就想到了排序,这样每个数可能的好对就是它和它两边的两个数。
举个栗子:
$$3,9,11,4,8,6$$
编号
$$1,2,3,4,5,6$$
排序过后就变成
$$3,4,6,8,9,11$$
对应的编号是
$$1,4,6,5,2,3$$
对于每一个数,判断一下它与它左右两边的数的差的绝对值:
- 如果相等,那么就是两个好的配对(左右两边都是好对),以6为例:
$\left\vert 6-4\right\vert = \left\vert 6-8\right\vert$ 6和4对应的好对为 $(6,4)$ ,6和8对应的好对为 $(6,5)$。
- 如果不相等,那么只有绝对值之差更小的一对,以4为例:
$\left\vert 4-3\right\vert < \left\vert 4-6\right\vert$ 只有4和3的好对 $(4,1)$ 。
- 当然两边的数只有唯一的一对
3和4对应 $(1,4)$ ,11和9对应 $(3,2)$。
注:为方便以后查询,统一把好对中出现位置较小的那个放在前面(就是说6和8对应的好对 $(6,5)$ 记为 $(5,6)$ )。
要注意的是,如果一个配对 $(x,y)$ 是好对, $(y,x)$ 不一定是好对,如9和11: $(3,2)$ 是好对,而 $(2,3)$ 就不是。
数据约束中说到当$i \ne j,a_i \ne a_j$,即$a$中没有相同的元素,这样就保证了这个配对判断的正确性。
至此我们已经找到了所有的配对,时间复杂度 $O(n \log n)$ (瓶颈在排序)。
### 查询所有询问
每次询问都是区间查询,很容易想到树状数组(当然还有线段树),也就是查询所有左右端点都在$[l,r]$内的好对。
但是怎么查呢?
请仔细思考后再继续阅读。
------------
你会发现,如果把所有的好对都放进树状数组里不太好查。
那我们就不要一次性把所有的好对都放进去呗。
也就是说,对于每次查询,我们只把右端点在 $(0,r]$ 内的好对放进树状数组。
树状数组 $tree[i]$ 表示左端点在 $[i-\operatorname{lowbit}(i)+1 , i]$ 内的所有好对的的个数。
已经放入的好对个数,减去左端点在 $(0,l-1]$ 内的好对(也就是减去 $\operatorname{query}(l-1)$ ),就可以得到答案了。
再举栗子:
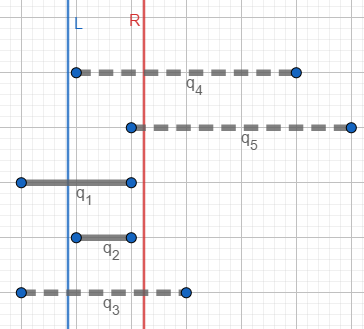
实线表示该好对在树状数组中,虚线表示该好对还未放入树状数组。
待查询的区间 $[L,R]$ 如图所示,此时只有 $q_1,q_2$ 两个好对在R左侧,再减去左端点在L左侧的 $q_1$ ,就得到 $[L,R]$ 内的好对数目:1个( $q_2$ )。
我们再将所有的好对和所有的询问,都按右端点从小到大排个序。
每次R右移,就将右端点小于等于R的所有好对,都加入到树状数组里,再减去左端点在 $(0,l-1]$ 内的好对个数就是答案。
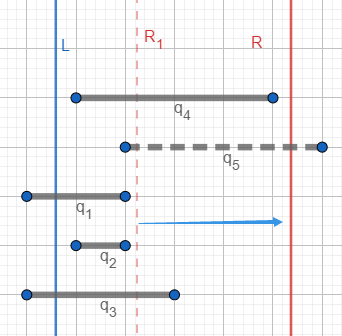
此时R右移, $q_3,q_4$ 被放入树状数组,再减去左端点在L左侧的 $q_1,q_3$ ,就得到 $[L,R]$ 内的好对数目:2个($q_2,q_4$)。
遍历每个询问$O(n)$,每次查询$O(\log n)$,总时间复杂度$O(n \log n)$。
### 统计答案
因为答案的计算方法很~~奇葩~~特殊, $\sum\limits_{i=1}^mAns_i \times i$ 。
所以我们在给询问排序的时候也要记录下它原先的 $i$ (代码中为 $pos$ )。
$Ans_i$ 的计算方法上文已经讲得很清楚了,这里不再多说。
整体时间复杂度 $O(n \log n)$ 。
#### 亲身经历告诉你们一定要开long long!!!
## 关于hack
新增的hack中 $n=1$,如果不特判的话会出现 $i+=lowbit(i)$ 而 $i=0$,从而死循环,下面的代码已经可以通过 hack
## 上代码:
```cpp
#include <iostream>
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
int lowbit(int x){ return x & (-x);}
int n,m;
ll tree[300001];
void add(int pos){ //单点修改(每次只用加1)
while(pos<=n)
tree[pos]++,pos+=lowbit(pos);
}
int Query(int num){
ll sum=0;
while(num>0)
sum+=tree[num],num-=lowbit(num);
return sum;
}
//以上为树状数组的单点修改区间查询
struct Num{
ll num; int pos; //原数组
}a[300001];
bool cmp(Num a1,Num a2){return a1.num<a2.num;} //结构体排序
struct Pair{
int l,r; //好对
}pairr[600002];
int paircnt=0; //记录好对个数
void add_pair(Num a1,Num a2){
int l=min(a1.pos,a2.pos) , r=max(a1.pos,a2.pos);
//为了方便查询,统一把好对中出现位置较小的那个放在前面
pairr[++paircnt].l=l;
pairr[paircnt].r=r;
return ;
}
bool cmpPair(Pair a1,Pair a2){ //对所有的好对按右端点从小到大排序
if(a1.r!=a2.r) return a1.r<a2.r;
else return a1.l<a2.l;
}
struct Questions{
int l,r,pos; //询问
}question[300001];
bool cmpQestions(Questions a1,Questions a2){ //对所有的询问按右端点从小到大排序
if(a1.r!=a2.r) return a1.r<a2.r;
else return a1.l<a2.l;
}
int main(){
scanf("%d %d",&n,&m);
if(n==1){puts("0");return 0;}//新增的hack
for(int i=1 ; i<=n ; i++){
scanf("%lld",&a[i].num);
a[i].pos=i; //记录下该数在原先序列里的位置,排完序后方便添加配对
}
sort(a+1,a+1+n,cmp); //排序
add_pair(a[1],a[2]); //首位特殊处理
add_pair(a[n],a[n-1]); //末尾特殊处理
for(int i=2 ; i<n ; i++){
int ldif = a[i].num-a[i-1].num , rdif = a[i+1].num-a[i].num; //左边的差 和 右边的差
if(ldif<rdif) add_pair(a[i],a[i-1]); //左边差更小,只有左边的一对
else if(ldif==rdif) add_pair(a[i],a[i-1]),add_pair(a[i],a[i+1]);
//两边差更小,有两对
else add_pair(a[i],a[i+1]); //右边差更小,只有右边的一对
}
sort(pairr+1 , pairr+1+paircnt , cmpPair); //对所有的好对按右端点从小到大排序
for(int i=1;i<=m;i++){
scanf("%d %d", &question[i].l ,&question[i].r);
question[i].pos=i;
}
sort(question+1 , question+1+m , cmpQestions);//对所有的询问按右端点从小到大排序
ll ans=0; //ans为最终答案
for(int i=1,j=1 ; i<=m ; i++){ //i为当前询问,j为当前待入树状数组的好对
while(pairr[j].r<=question[i].r && j<=paircnt){
add(pairr[j].l); //如果当前好对的右端点在当前询问的右端点内,就加入树状数组
j++;
}
ans+=1ll * question[i].pos * (j-1- Query(question[i].l-1) ); //计算答案
}
printf("%lld",ans); //输出
return 0;
}
```