考虑到每个云朵的运动周期都是 2len(经过 2len 的时间之后回到原处),我们可以把每个云彩在位置-时间坐标系里画成一个图形:横坐标是位置;纵坐标是时间,而纵坐标的取值范围只有 [0,2len]。一个点 (x,T) 在这个图形里当且仅当 T 时刻时 x 这个位置能接到这个云朵(假定线段的出现时间比 T 早)。
比如样例 1,len=10,一个区间在时刻 0 出现在
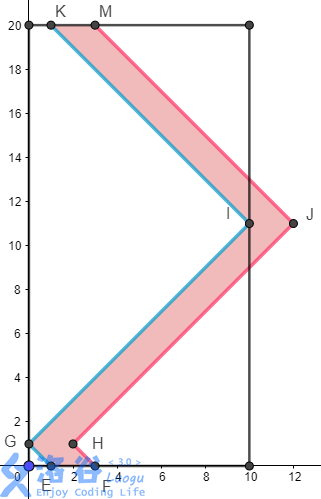
如果这个区间是在时刻 25 出现在 $[4,6]$ 并往右移动,那它对应的图形是一样的。
一般的,如果一个区间在 $0$ 时刻(注意,时间对 $2len$ 取模,相当于在 $2k\cdot len$ 时刻)处于 $[l,r]$ 且向左走,那么蓝折线为 $(l,0)-(0,l)-(len,len+l)-(l,2len)$,红折线的四个点分别是蓝折线四个点向右平移 $r-l$;如果这个区间在 $0$ 时刻处于 $[l,r]$ 且向右走,那蓝折线就是 $(l,r)-(len,len-l)-(0,2len-l)-(l,0)$,红折线同上。
我们把图中的蓝色折线 KIGE 称作图形的“左边界”,红色折线 MJHF 称作其“右边界”。
一个 $T$ 时刻出现的询问区间 $[l,r]$ 可以对应图中的一条水平线段 $(l,T)-(r,T)$;显然这个布袋能接到这个云彩当且仅当这个线段和上图的图形相交;这等价于说 $(l,T)$ 在右边界左边并且 $(r,T)$ 在左边界右边(可以恰好在边界上)。
这启示我们把询问拆开:询问右端点在多少图形的蓝折线右边(包括在折线上),再询问左端点在多少图形红折线的右边(不包括在折线上);两者相减就是答案。(如果你无法理解的话,想一想云彩改成不动的怎么做就知道了)
显然两个问题是对称的,我们只考虑如何求前者(给定坐标系里一点问它在多少蓝折线右边)。
如果蓝色折线只由水平和竖直的线段组成的话我们可以把它拆成若干矩形从而使用二维树状数组解决;但是现在线段都是倾斜 $45^\circ,135^\circ$ 的。
可以想到旋转坐标系。如果我们把坐标系旋转 $45^\circ$,如下图
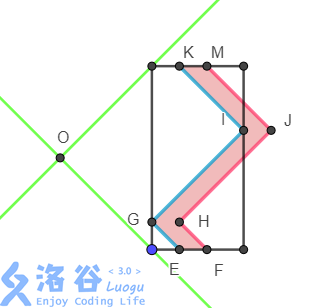
选取点 $O(-len,len)$ 为原点(其实哪里都无所谓的),两条绿色线是新坐标轴。不难发现这样处理之后红折线和蓝折线在新坐标系里是水平和竖直线段组成的(请倾斜 $45^\circ$ 看)。
设原坐标为 $(x,T)$,新坐标为 $X,Y$,可以发现换算规则是(如果要求长度不变的话实际上有 $\frac1{\sqrt2}$ 的系数,但是既然我们只需要知道相对位置关系,所以无所谓了)
$$\left\{\begin{aligned}X&=x-T+2len\\Y&=x+T\end{aligned}\right.$$
所以现在问题变成:在新坐标系里每次添加或删除一条像图中蓝折线那样的线,以及对一个点问它在多少折线的右侧(或者上侧,感性理解一下)。
利用二维树状数组,我们添加图中蓝折线的时候只需要在 $K,G$ 处各加一、在 $I$ 处减一;但是我们发现不会有点处在 $I$ 的右上侧($I$ 点本身除外,可以特判一下),所以只需要在 $K,G$ 点各加一即可;红折线也完全相同。
于是这题在 $O(n\log^2len)$ 的时间内解决。
上代码(CDQ分治,并非二维树状数组,空间 $O(n+len)$):
```cpp
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
const int L = 2050;
const int N = 200050;
const int C = 1000050;
int m, len, cl[C], cr[C], cd[C], ans[N], k;
int P[L * 2];
int readInt() {
int ans = 0, c, f = 1;
while (!isdigit(c = getchar()))
if (c == '-') f = -1;
do ans = ans * 10 + c - '0';
while (isdigit(c = getchar()));
return ans * f;
}
struct Event {
int tp, x, y, id;
Event() {}
Event(int t, int X, int T, int id = 0)
: tp(t), x(X - T + 2 * len), y(X + T), id(id) {
}
friend bool operator<(const Event &a, const Event &b) {
if (a.x != b.x) return a.x < b.x;
return a.y < b.y;
}
} e1[N * 2], e2[N * 2];
int S[L * 3], ll;
void add(int x, int y) { for (++x; x <= ll; x += x & -x) S[x] += y; }
int get(int x) { int y = 0; for (++x; x; x &= x - 1) y += S[x]; return y; }
void Solve(Event *e, int l, int r) {
if (l == r - 1) return;
int mid = (l + r) / 2;
Solve(e, l, mid);
Solve(e, mid, r);
for (int i = l, j = mid; i < mid || j < r; ) {
if (i < mid && (j == r || e[i].x <= e[j].x)) {
if (e[i].tp) add(e[i].y, e[i].tp);
++i;
} else {
if (!e[j].tp) ans[e[j].id] += get(e[j].y);
++j;
}
}
for (int i = l; i < mid; ++i)
if (e[i].tp) add(e[i].y, -e[i].tp);
std::inplace_merge(e + l, e + mid, e + r);
}
inline void eventAdd(int L, int R, int D, int tp) {
if (D == 1) {
e1[m] = Event(tp, L, 0);
e1[m + 1] = Event(tp, 0, 2 * len - L);
P[len - L] -= tp;
e2[m] = Event(-tp, R, 0);
e2[m + 1] = Event(-tp, R - L, 2 * len - L);
} else {
e1[m] = Event(tp, 0, L);
e1[m + 1] = Event(tp, L, 2 * len);
P[len + L] -= tp;
e2[m] = Event(-tp, R - L, L);
e2[m + 1] = Event(-tp, R, 2 * len);
}
m += 2;
}
inline void eventQuery(int L, int R, int T, int i) {
e1[m] = Event(0, R, T, i);
e2[m++] = Event(0, L - 1, T, i);
if (R == len) ans[i] += P[T];
}
int main() {
int n = readInt();
len = readInt();
while (n--) {
int op = readInt(), T = readInt() % (2 * len);
if (op == 1) {
int C = readInt(), L = readInt(), R = readInt() - L, D = readInt();
for (L -= T * D; L < 0 || L > len; D = -D)
L = L < 0 ? -L : 2 * len - L;
eventAdd(L, R += L, D, 1);
cl[C] = L;
cr[C] = R;
cd[C] = D;
} else if (op == 2) {
int L = readInt(), R = readInt();
eventQuery(L, R, T, k++);
} else {
int C = readInt();
eventAdd(cl[C], cr[C], cd[C], -1);
}
}
ll = len * 3;
Solve(e1, 0, m);
Solve(e2, 0, m);
for (int i = 0; i < k; ++i)
printf("%d\n", ans[i]);
return 0;
}
```