【题解】P10230 [COCI 2023/2024 #4] Lepeze
AFewSuns
·
·
题解
题目大意
给定一张三角剖分图,外圈按顺序标号为 1\sim n。定义一次操作为删除一条边,再加入一条边得到一个新的三角剖分。
有 q 次修改或询问,每次会进行一次合法操作,或询问一个点 x,求最少进行多少次操作使得所有对角线都有共同端点 x,以及达到最少操作次数的方案数。
### 题目分析
首先操作数的下界就是顶点不含 $x$ 的对角线个数,而事实上这个下界很容易取到,所以只需要考虑方案数。
按照这个下界手玩一下,便可以发现新增边的加入顺序会有一定的先后关系,即加入某条边之前必须先加入另一条边:
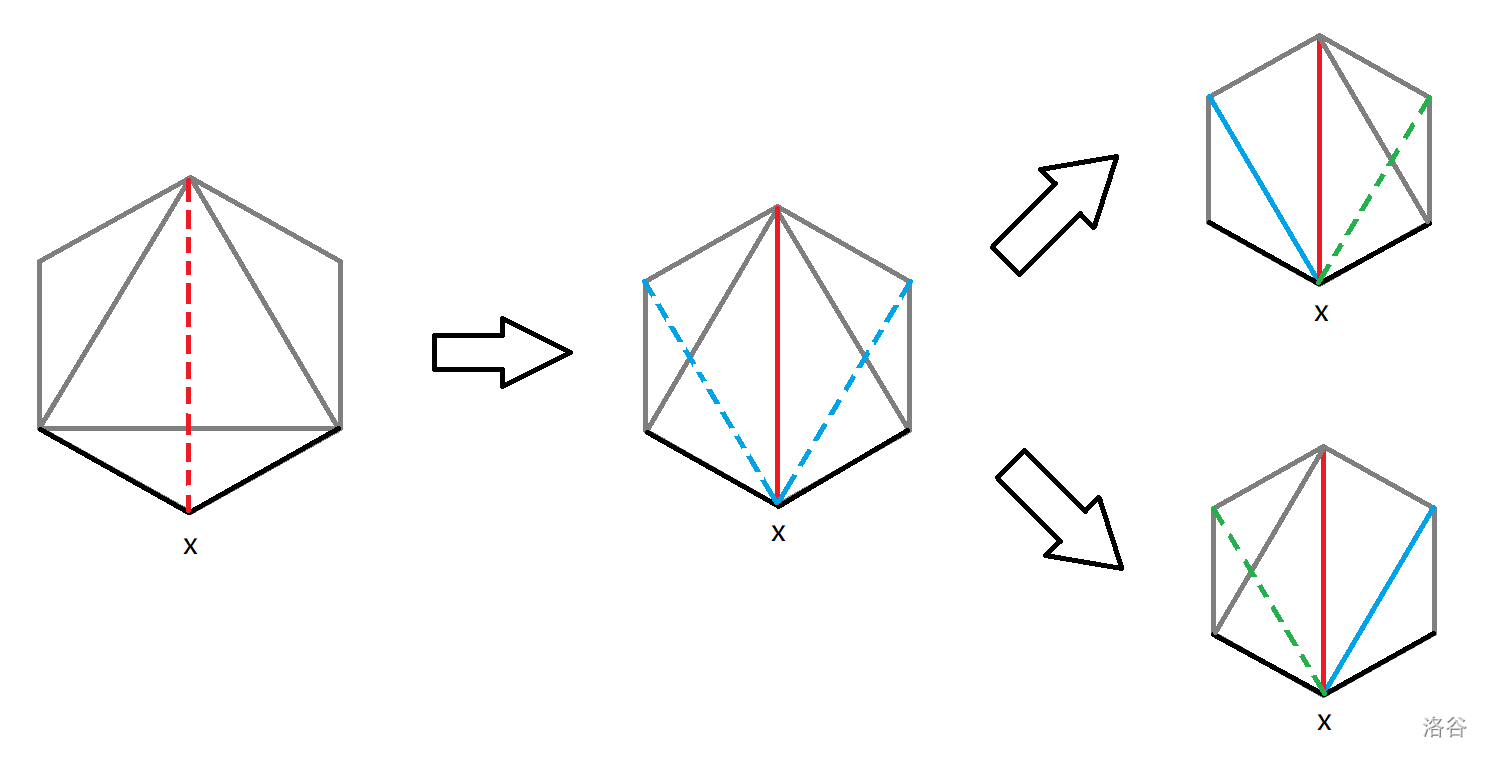
如图,只有在加入红色边之后才能加入另外两条边,故方案数为 $2$。
以此类推,可以发现其先后顺序会形成一种树形结构,必须按照树的拓扑序进行加边:
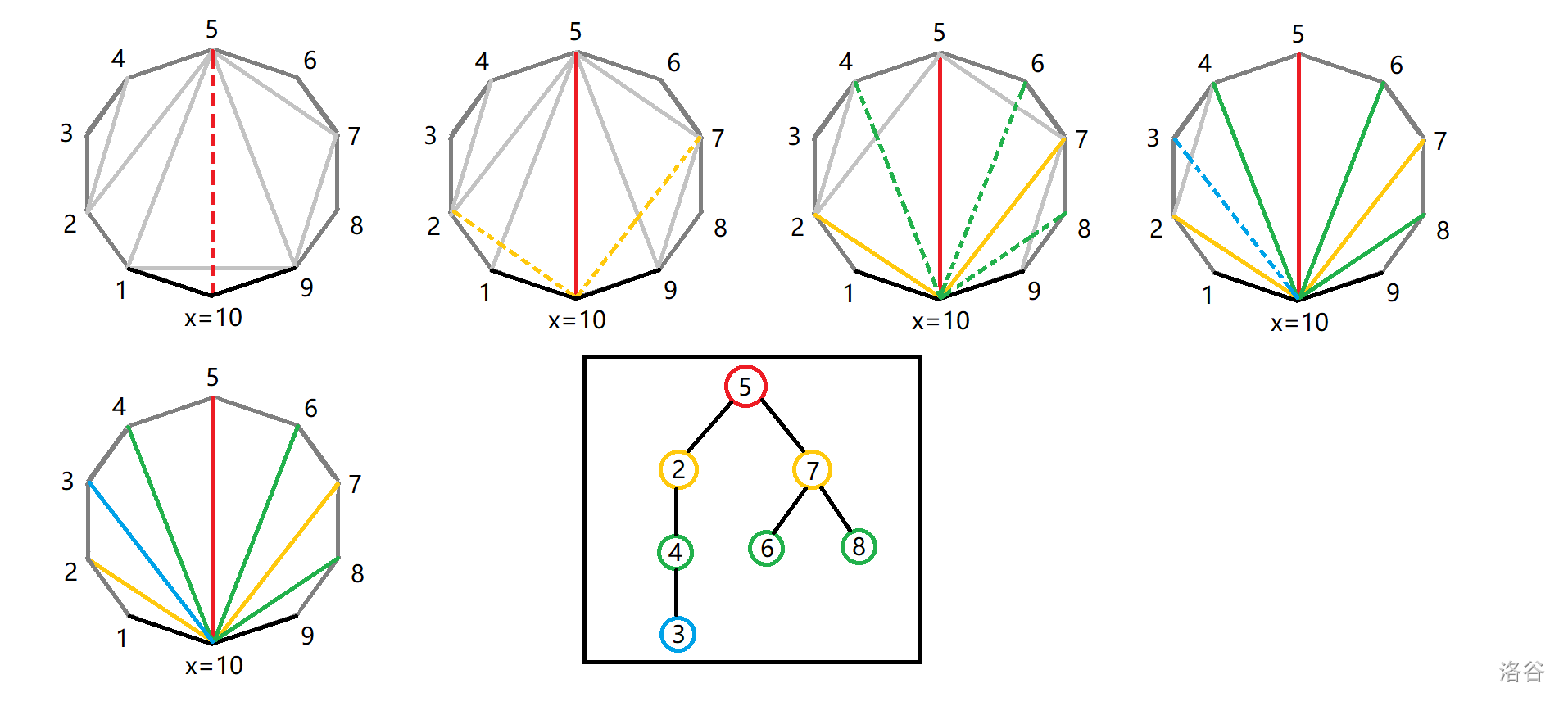
其中不交的两棵子树之间互相独立(中间的边会将两边分开),于是方案数即为这棵树的拓扑序个数。
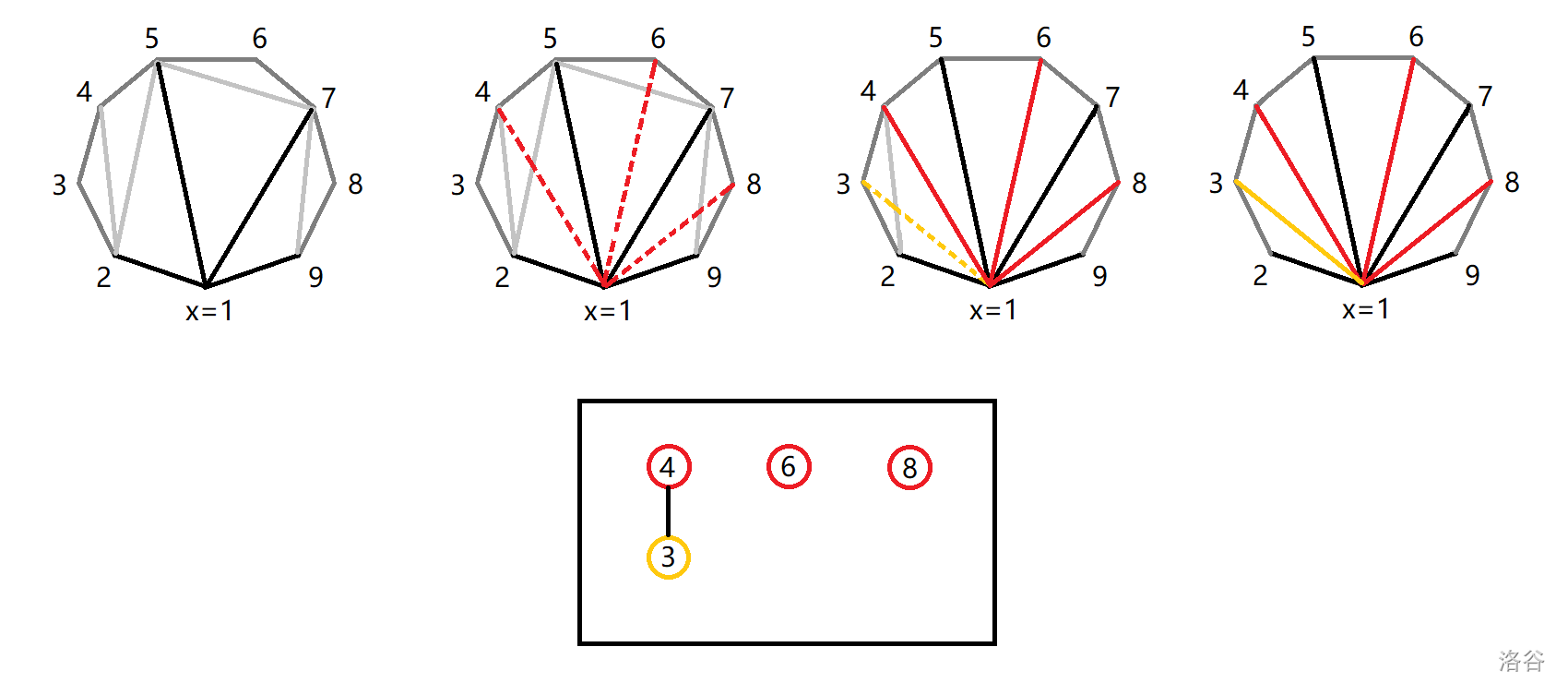
上图为样例二的示意图。可以发现,当初始有对角线顶点包含 $x$ 的时候,这些对角线划分出来的区域互相独立,最终也会形成若干棵树。
而树的拓扑序方案数即为 $\dfrac{n!}{\prod\limits_{i=1}^{n}{siz_i}}$,其中 $siz_i$ 为 $i$ 子树的大小,$n$ 为总节点个数,在题目中的显现即为第一问(最少操作次数)的答案。
考虑如何在原图中快速刻画这棵树。将三角剖分形成的树画出来:
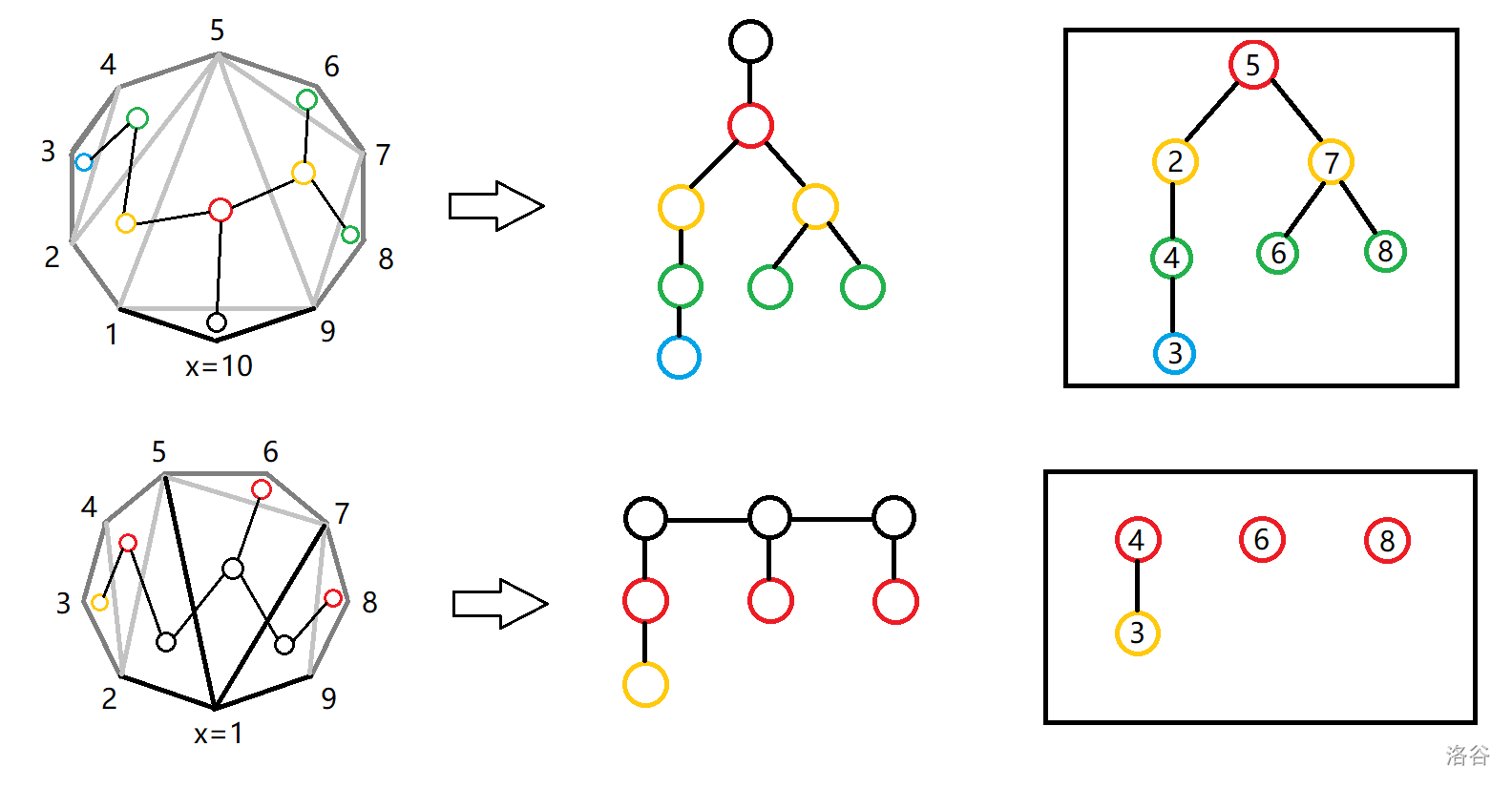
对比发现除去黑点之后,这就是我们想要的树,而黑点就是相邻两个顶点包含 $x$ 的边中间夹成的三角形。证明比较容易,在此省略。
于是现在的主要问题在于如何维护 $\prod\limits_{i}{siz_i}$,修改就相当于删边加边。考虑树上的一个点(非黑点)及其子树,它在原图上其实代表着一段完整圆弧,设其为 $[l,r]$,那么这个子树的大小即为中间剖出来的三角形个数,为 $r-l-1$。而它是非黑点的条件也很简单,即 $[l,r]$ 不能包括 $x$。
现在这道题的做法已经呼之欲出了:对于每条对角线 $(x,y)$,将没被 $x\to y$ 这段圆弧包含的点除以 $len_{x\to y}-1$;将没被 $y\to x$ 这段圆弧包含的点除以 $len_{y\to x}-1$。这是一个区间乘,单点查询问题,使用树状数组即可做到 $\mathcal O((n+q)\log n)$。
### 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
using namespace my_std;
#define mod 1000000007
ll n,q,jc[200020],jcinv[200020],invv[200020],sum[200020],tree[200020];
il ll lowbit(ll x){
return x&(-x);
}
il void mdf(ll x,ll v){
if(v<0) v=-v;
else v=invv[v];
while(x<=n){
tree[x]=tree[x]*v%mod;
x+=lowbit(x);
}
}
il ll query(ll x){
ll res=1;
while(x){
res=res*tree[x]%mod;
x-=lowbit(x);
}
return res;
}
il void solve(ll x,ll y,ll t){
sum[x]-=t;
ll len=(y-x+n)%n-1;
swap(x,y);
x=x%n+1;
y=(y+n-2)%n+1;
if(x<=y){
mdf(x,t*len);
mdf(y+1,-t*len);
}
else{
mdf(x,t*len);
mdf(1,t*len);
mdf(y+1,-t*len);
}
}
int main(){
n=read();
q=read();
jc[0]=1;
fr(i,1,n) jc[i]=jc[i-1]*i%mod;
jcinv[n]=inv(jc[n],mod);
pfr(i,n-1,0) jcinv[i]=jcinv[i+1]*(i+1)%mod;
fr(i,1,n) invv[i]=jcinv[i]*jc[i-1]%mod;
fr(i,1,n) sum[i]=n-3;
fr(i,1,n) tree[i]=1;
fr(i,1,n-3){
ll x=read(),y=read();
solve(x,y,1);
solve(y,x,1);
}
while(q--){
ll opt=read();
if(opt==1){
ll x=read(),y=read(),xx=read(),yy=read();
solve(x,y,-1);
solve(y,x,-1);
solve(xx,yy,1);
solve(yy,xx,1);
}
else{
ll x=read();
pf("%lld %lld\n",sum[x],jc[sum[x]]*query(x)%mod);
}
}
}
```