题解:AT_arc024_2 [ARC024B] 赤と黒の木
残阳如血
·
·
题解
参考了官方题解的思路和一张图片。
\textbf{Description}
下面为形式化题意。
有一个长度为 n 的 01 序列 a,数组下标循环。
定义一次操作为 \forall\,i\in[1,n],若 a_{i-1}=a_{i}=a_{i+1},则修改 a_i 为另一个值(0 或 1)。
求最少的操作次数,使得下一次操作中 a 不会发生变化(即稳定)。
**注意,在一次操作中,$a_i$ 的变化不会影响后续修改**(即对 $a_i$ 的修改在当前操作结束后才生效)。
### $\textbf{Solution}
直接讲正解。
下面假定 $0,1$ 为不同颜色的球。~~其实是为了方便把照片搞过来。~~
> 考虑一种情况。
>
> 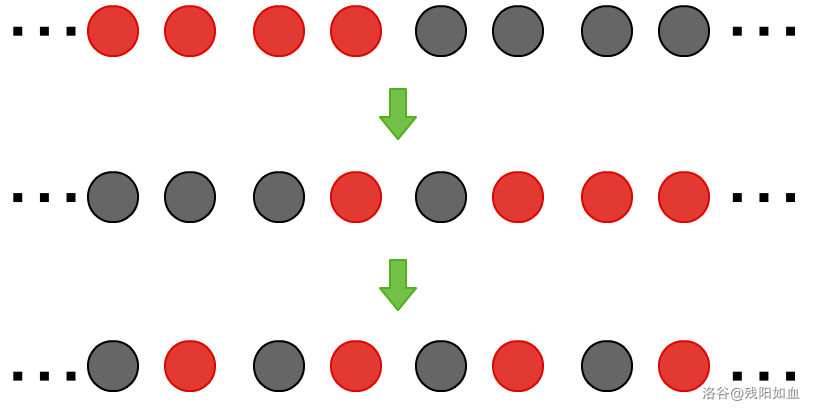
> (假设左边有 $\infty$ 个红色球,右边有 $\infty$ 个黑色球)。
>
> 根据上图可以发现,没有任何操作跨越了初始红、黑球的分界线,所以左边和右边是独立的。
那么,我们就可以用不同颜色的球之间的分界线破环成链。
当然,如果找不到分界线,即序列中都是同一个数,则序列会永远变化下去,输出 $-1$。
容易发现,此时序列变为 $0,0,\cdots,0,1,1,\cdots,1,0\cdots$(假设开头元素为 $0$),分成了好几个 $0$ 和 $1$ 的块。
---
由于各个块之间相互独立,所以我们可以分别考虑。
根据块长 $l$ 奇偶性分类讨论。
- $l$ 为偶数:
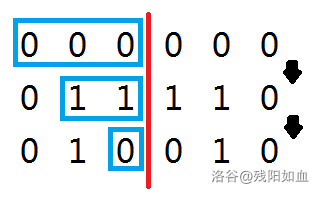
考虑前 $\dfrac{l}{2}$ 个数,可以发现被修改的部分由 $\dfrac{l}{2}$ 变为 $1$(假设初始是由空数组修改得到的),那么操作了 $\dfrac{l}{2}$ 次,稳定的天数为 $\dfrac{l}{2}$。
- $l$ 为奇数:
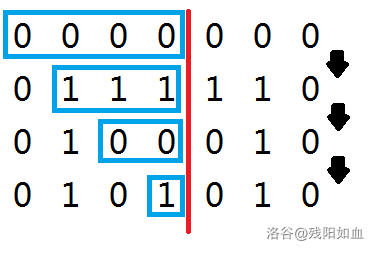
此时考虑前 $\dfrac{l+1}{2}$ 个数,可以得出稳定的天数为 $\dfrac{l+1}{2}$。
将两者结合,可以发现稳定所需要的天数为:
$$
\left\lfloor\dfrac{l+1}{2}\right\rfloor
$$
---
此时做法呼之欲出了。
1. 读入,将 $a$ 序列复制并接到最后;
2. 得到 $0$ 和 $1$ 块的分界线;
3. 对于每个块,统计长度并根据公式计算;
4. 每个块稳定所需的天数最大值即为所求。
### $\textbf{Code}
数组一定要开到 2\times10^5!
数组一定要开到 2\times10^5!
数组一定要开到 2\times10^5!
record。
#include <bits/stdc++.h>
const int N = 2e5 + 10; // 数组开两倍!
int n, p, ans, cnt = 1, a[N];
/*
n:输入的序列长度
p:0 和 1 块的任一分界线
ans:最终答案
cnt:当前统计块的长度(初始值为 1 是因为预先将 a[p] 放入)
a:序列
*/
int main() {
std::cin >> n;
for (int i = 1; i <= n; ++i) {
std::cin >> a[i], a[i + n] = a[i]; // 复制并放到后面
if (i > 1 && a[i] != a[i - 1]) p = i; // 找到分界线
}
if (!p) return std::cout << "-1\n", 0; // 找不到分界线
for (int i = p + 1; i <= n + p; ++i) {
if (i > p && a[i] == a[i - 1]) ++cnt; // 在同一个块中
else ans = std::max(ans, cnt + 1 >> 1), cnt = 1; // 统计答案,重置计数器
}
std::cout << ans << std::endl;
return 0;
}