P7915/2021CSPST3题解
Danno0v0
·
·
题解
感谢机房大佬@嘉年华让这个 O(n^2) 的暴力优化到了近似于 O(n) (可恶为什么我没在考试的时候优化出来)
然后这个题解思路清奇(就是暴力加上了一堆优化然后跑过了),相较于 std 可能会有所不同。
首先一看,回文,好耶, Hash —— 然而并不是。
众所周知,了解一道题的最好方法就是手推样例(瞎说的),所以我们来手推一下。
样例一的第一组数据的 a 和 b:
然后手模一下怎么生成 b 的:
嗯,连得密密麻麻的不想看,做 T4 去了。
这当然是不可以的,但是这样看确实看不出来什么东西。
想一下题上有什么提示……
b 是一个回文数列。
既然 b 是一个好观察的回文数列那就从 b 入手吧。

好像也没有什么。
不对,看一看后半段 $b$ 。
这是由连续的一段 $a$ 组成的。
想一想,不论什么 $b$ 的后半段都是由 $a$ 中一段连续的,长度为 $n$ 的数列组成的。
就像这样:

(长度不准确请忽视)
有了这个,我们就可以开始我们优雅の暴力了。
1.暴力枚举每一个后半段区间位置。
2.判断是否合法。
3.输出。
然后这个时候有人就会跑上来说,你这个暴力是 $O(n^3)$ 的啊不是 $O(n^2)$ 的啊。
( $n^3$ : 枚举 $n$ 个区间、记录每个区间 $n$ 个数,判断是否合法要 $n$ 次判断)
所以我们需要对暴力进行优化。
### 优化一
首先我们想,一个后半段区间假若有机会成为解,那么必要条件是……
当然是这个区间里包含了 $1,2,...,n$ 啦(不然你怎么回文)。
那么我们在枚举一个后半段区间时可以顺便来看看它是否包含了 $1,2,...,n$ ,没有则直接跳到下一个区间,否则来判断是否合法以及假如合法则方案是否是字典序最小的。
当然这个优化对于随机数据收益巨大,能大幅消减判断的 $n$ 以至于能看成 $O(n^2)$ ,因为减少了很多不必要的判断;但是对于构造的数据,比如说这个:
$1,2,...,10000,1,2,...,10000
那这个优化就什么用都没有,直接退化 O(n^3) 。
优化二
所以再来一个显而易见的优化:每个区间都是在上一个区间基础上挪了一个罢了,所以可以直接在上一个区间的基础上进行改动,这样就把记录每个区间的数的 n 就消掉了,这样就是一个完全的 O(n^2) 暴力了。加上前面的优化,对于随机数据能直接跑到近似于 O(n) 乘上一个大常数。
```cpp
#include<bits/stdc++.h>
using namespace std;
int t,n,tot,now,check,qrs;
int num[1000001],cnt;
int in[1000001];
char ans[1000001],maybeans[1000001];
stack<int>castle_3;
stack<int>lancet_2;
int main()
{
// freopen("palin.in","r",stdin);
// freopen("palin.out","w",stdout);
cin>>t;
while(t--)
{
memset(ans,0,sizeof(ans));
memset(in,0,sizeof(in));
cnt=0;
qrs=0;
cin>>n;
for(int i=1;i<=2*n;i++)
{
cin>>num[i];
}
int l=1,r=n;
for(int i=l;i<=r;i++)
{
in[num[i]]++;
if(in[num[i]]==1)
{
cnt++;
}
}
while(r<=2*n)
{
if(cnt==n)
{
memset(maybeans,0,sizeof(maybeans));
check=0;
for(int i=1;i<l;i++)
{
castle_3.push(num[i]);
}
for(int j=2*n;j>r;j--)
{
lancet_2.push(num[j]);
}
int ll=l,rr=r;
int a,b;
int now=0;
while(ll<=rr)
{
a=-1;
b=-1;
if(castle_3.size()) a=castle_3.top();
if(lancet_2.size()) b=lancet_2.top();
if(b==num[ll])
{
maybeans[n-now]='R';
maybeans[n+1+now]='L';
lancet_2.pop();
now++;
ll++;
}
else if(b==num[rr])
{
maybeans[n-now]='R';
maybeans[n+1+now]='R';
lancet_2.pop();
now++;
rr--;
}
else if(a==num[ll])
{
maybeans[n-now]='L';
maybeans[n+1+now]='L';
castle_3.pop();
now++;
ll++;
}
else if(a==num[rr])
{
maybeans[n-now]='L';
maybeans[n+1+now]='R';
castle_3.pop();
now++;
rr--;
}
else
{
check=1;
break;
}
}
if(!check)
{
if(!qrs)
{
for(int i=1;i<=n*2;i++)
{
ans[i]=maybeans[i];
}
qrs=1;
}
else
{
int i=1;
int checks=0;
for(;i<=n*2;i++)
{
if(ans[i]!=maybeans[i])
{
checks=1;
break;
}
}
if(maybeans[i]=='L'&&checks)
{
for(int j=1;j<=n*2;j++)
{
ans[j]=maybeans[j];
}
}
}
}
while(!lancet_2.empty()) lancet_2.pop();
while(!castle_3.empty()) castle_3.pop();
}
in[num[l]]--;
if(!in[num[l]]) cnt--;
l++;
r++;
in[num[r]]++;
if(in[num[r]]==1) cnt++;
}
if(!qrs)
{
cout<<-1<<endl;
}
else
{
for(int i=1;i<=n*2;i++)
{
cout<<ans[i];
}
cout<<endl;
}
}
}
```
_判断可行性解释:用两个栈记录左边前半部分与右边前半部分,然后和后半部分尝试匹配。每匹配成功就把它们加入maybeans方案中。对于这个“匹配”,请好好读读,因为后半段优化是基于这个“匹配”的。_
_代码解释: in 数组是用来记录区间内所有数的个数, cnt 是用来记录区间内有多少个不同的数;对于 in 和 cnt 的变化规律为什么是这样,手推一遍就很容易明白。然后是让每个区间生成最优解:因为我们需要让操作 $R$ 尽可能在后,那么我们就先让 前半部分的右端先进行匹配,这样对于每个枚举的后半段区间,生成的答案就是局部最优解_
然后机房大佬 FJN 因为没有打出暴力 T3 感到非常悲伤,然后听说我打出了一个随机化数据能跑 $O(n)$ ,构造能跑 $O(n^2)$ 的暴力于是来找我看看代码。
看着看着然后他就来了一句:你这个可以再优化成 $O(n)$ 的。
对,这就是最后一个优化。
### 优化三
概括一下就是:倒序枚举后半段区间,当找到第一个解时就一定是最优解。
为甚么呢?
首先我们想一个基础事实:假如 $a$ 中有 $2$ 个或以上的符合要求的后半段区间,那么它们一定是有重合部分的。
(例外: $1,2,3,1,2,3$ 中前一个 $1,2,3$ 和后一个 $1,2,3$ 不重合,但是看一眼就知道选后面一个答案更优。)
就像这样:
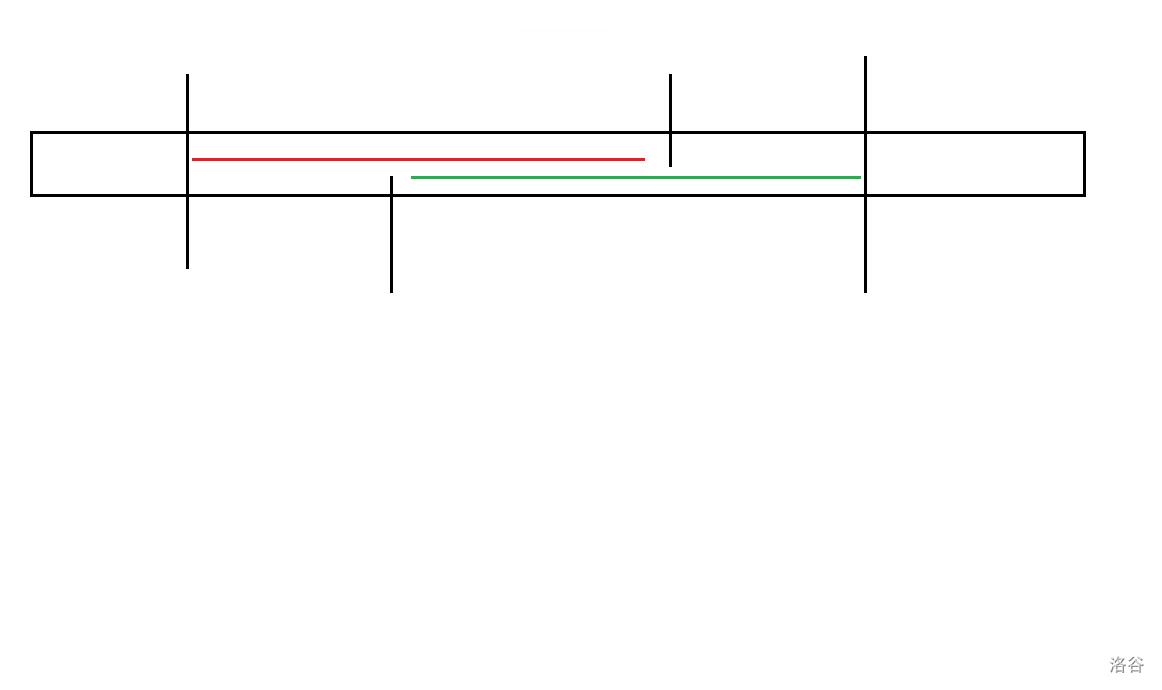
为什么会重合?因为两段区间都包含 $1$ 至 $n$ 中所有数,而 $1$ 至 $n$ 每个又只有两个,所以一定会重合。
上图的红绿线段就是两个符合要求的后半段区间,那么显而易见的可以知道,没有重叠的部分是相同的。(你问为什么? $A-B=A-B$ )
那么,在进行回文配对时,红色没有重叠部分一定是跟绿色没有重叠部分进行配对。毕竟含有相同的数。
那么,假若我们选择红色作为后半段区间,那么绿色的未重叠部分则是用 $R$ 操作弹出。(假如可行)
假若我们选择绿色作为后半段区间,那么红色的未重叠部分则是用 $L$ 操作弹出。(假如可行)
回看匹配过程,不管我们选择红色还是绿色,我们一定是先将不属于红色或绿色的是跟红绿重合部分匹配(你不把它们匹配完怎么匹配中间的啊),那么它们的在方案中位置及方案是固定的,那么就剩红色和绿色不重叠部分了。
假如我们选择是红色且红色可行,那么在这里我们会全部用 $R$ 进行剩余匹配。
假如是绿色且绿色可行,那么在这里我们会全部用 $L
进行剩余匹配。
显而易见的,绿色更优。
所以两段后半部分区间都可行时,那么选择后面那段作为后半区间更优。
于是乎,倒着枚举区间,遇到第一个可行的区间就输出答案,正确性证明完毕,于是就开心滴砍掉了大部分判断这个 n 。结合前面的优化,一个近似于 O(n) 就这么搞出来啦~
当然,如果真的要专门构造数据来卡当然是可以退化到 O(n^2) 的(悲)
```cpp
#include<bits/stdc++.h>
#define ooffof 1000001
using namespace std;
int t,n,tot,now,check,qrs;
int num[ooffof],cnt;
int in[ooffof];
char ans[ooffof],maybeans[ooffof];
int l[ooffof],r[ooffof],klk=0;;
int main()
{
// freopen("palin.in","r",stdin);
// freopen("palin.out","w",stdout);
cin>>t;
while(t--)
{
memset(ans,0,sizeof(ans));
memset(in,0,sizeof(in));
cnt=0;
qrs=0;
klk=0;
cin>>n;
for(int i=1;i<=2*n;i++)
{
cin>>num[i];
in[num[i]]++;
if(in[num[i]]==1)
{
cnt++;
}
if(i>n)
{
in[num[i-n]]--;
if(in[num[i-n]]==0)
{
cnt--;
}
}
if(cnt==n)
{
l[++klk]=i-n+1;
r[klk]=i;
}
}
for(int q=klk;q>=1;q--)
{
memset(maybeans,0,sizeof(maybeans));
check=0;
int ll=l[q],rr=r[q],sl=l[q]-1,rl=r[q]+1;
int a,b;
int now=0;
while(ll<=rr)
{
a=-1;
b=-1;
if(sl>=1) a=num[sl];
if(rl<=2*n) b=num[rl];
if(b==num[ll])
{
maybeans[n-now]='R';
maybeans[n+1+now]='L';
rl++;
now++;
ll++;
}
else if(b==num[rr])
{
maybeans[n-now]='R';
maybeans[n+1+now]='R';
rl++;
now++;
rr--;
}
else if(a==num[ll])
{
maybeans[n-now]='L';
maybeans[n+1+now]='L';
sl--;
now++;
ll++;
}
else if(a==num[rr])
{
maybeans[n-now]='L';
maybeans[n+1+now]='R';
sl--;
now++;
rr--;
}
else
{
check=1;
break;
}
}
if(!check)
{
for(int i=1;i<=n*2;i++)
{
cout<<maybeans[i];
qrs=1;
}
cout<<endl;
}
if(qrs)
{
break;
}
}
if(!qrs)
{
cout<<-1<<endl;
}
}
}
```
~~好长的TJ~~