Trick:平面图转对偶图
hcx2012
·
·
算法·理论
一些奇葩定义:
:::info[定义[^1]]{open}
在一个平面上,如果能够画出无向图 G 的图解,其中没有任何边的交叉,则称图 G 是一个平面图;否则,称 G 是非平面图。
设平面图 G,其含有面 F_1,F_2\cdots ,F_n,包括有无限面,则可用以下方法构造 G 的对偶图 G^* :
在 F_i 内画出每个 F_i 对应的结点 v_i^*,并且连通 v_i^* 和 v_j^* ,去交叉 F_i 和 F_j 所有公共的边。易知
:::
很不像人话是吧?~我绝对不会告诉你我也没看懂。~
简单来说,一张图通过某种摆放方式使它的边互不相交,则它是一个平面图。
平面图的一个典型示例就是一个网格图。
:::align{center}
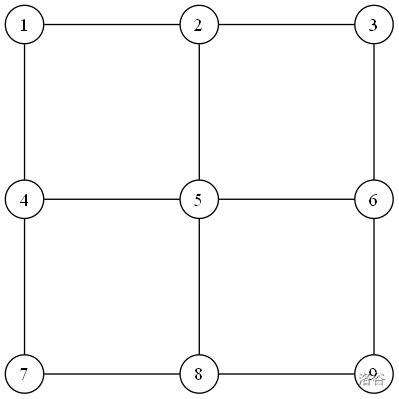
图 1:一张 $3\times 3$ 的网格图
:::
看到边与边之间围成的区域了吗?它们被称为一个“面”。(其中没有被图上的边围着、但被外边界围着、面积无限的区域叫做“无限面”)
我们把相邻的面与面连接起来,就成了对偶图。
:::align{center}
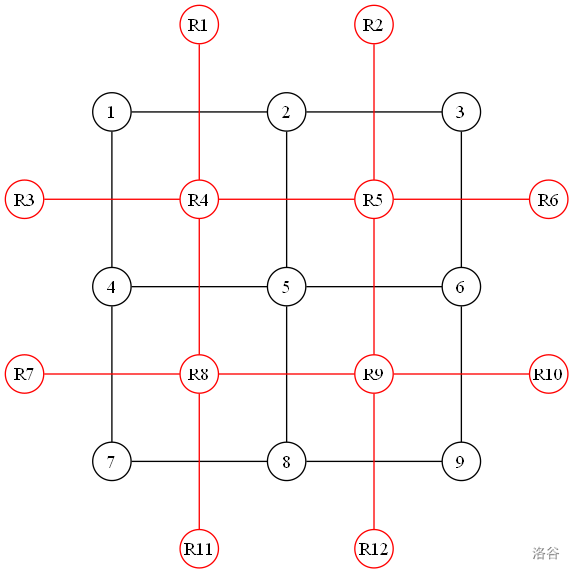
图 2:图 1 的对偶图,相对美化处理。
其中 R1、R2、R3、R6、R7、R10、R11、R12 均是无限面的“分身”。
:::
:::align{center}
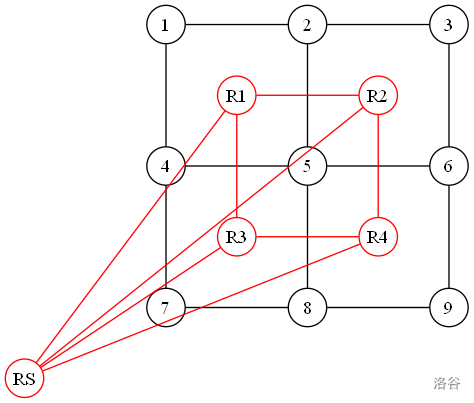
图 3:图 1 的对偶图,无特殊处理。
:::
我们发现,图 2 和图 3 虽然都是图 1 的对偶图,但图 2 更加清晰地反映出对偶图与原图的关联,所以之后本文的图片主要使用图 2 的样式,并会标明无限面的“分身”。
我们又发现,原图的每一条边有且仅对应一条对偶图上的边(下称对应边)。
对偶图的边权并不固定,换句话说,它只是一种“形状”,边权的规定需要因题而异。
## 例 1 无权无向平面图的最小割
我们还是以 $3\times 3$ 网格图为例(参考图 2),我们发现由于对偶图的每一条边都恰好交一个原图上的边,即对偶图上的边可以对应删掉对应边(的代价)。
连边跑一个最短路即可。注意我们需要克隆一个超级源点(即无限面对应的点出现两次)。
连出来的图接近于图 3,这里不再给图。
## 例 2 有权无向平面图的最小割(P4001)
例 1 中我们已经知道无权做法。对于有权图,做法类似。这里我们主要考虑边权如何赋。
可以非常简单地注意到边权赋原图的权值即可。注意刚才所述结论的括号部分:
> 对偶图上的边可以对应删掉原图上的边(**的代价**)。
所以同样只需要跑最短路即可。
## 例 3
考虑用这个 trick 做别的问题。
给一个 $n\times m$ 的网格图,$q$ 次询问,每次询问删掉 $(x_1,y_1)$ 与 $(x_2,y_2)$ 之间的边,在线询问此时的联通块个数。
$1\le nm\le 10^7$,$1\le q\le \min(mn,10^5)$,保证询问时边存在。
显然这个范围不能暴力。
但是,我们都会加边维护联通块——并查集。
继续之前的定义,对无权图,对偶图的边权是删掉对应边的代价。
我们维护一个空的对偶图,对每次操作加对偶图的边,即并查集的合并操作。
我们发现增加原图的联通块个数当且仅当合并时两个对偶图上的点已经在一个联通块内,而题目又保证询问合法,直接维护即可。
## 例 4 P7916 交通规划
题意已经很清楚了,这里不再多说。
看到网格图就想到建对偶图,我们就可以把染色时对点的操作转移到对边的操作。
观察到我们其实就是寻找若干条路径使附加点的颜色在每个路径分割出的空间中只有一种。
按照顺时针顺序排列附加点。遍历,遇到颜色不同的一对点就以它为源点跑一遍最短路。
最优的最短路一定不会相交,根据这个性质做一遍 dp 就求出了答案。
[^1]: 来自 <https://zhuanlan.zhihu.com/p/389763287>。