P2860 [USACO06JAN]Redundant Paths G 题解
Belarus
·
·
题解
Update 2020/11/22:修复了一个小错误。
Update 2021/09/30:修复了一个大错误,更新了更严谨的证明。
注意:本题解主要详细讲解为什么答案是 \lfloor\dfrac{s+1}{2}\rfloor(s 为叶子节点数)
首先我们要明白: 进行 e-DCC 缩点之后,最终形成的图是一棵树。
因为: 假设缩点之后的图不是树,那么一定存在一个环,因此这个环还可以缩成一个点,这产生了矛盾。
接下来讲解为什么是 \lfloor\dfrac{s+1}{2}\rfloor:
这个公式实际上是对 s 奇偶性的讨论得出来的通式。
先看 s 为偶数的情况。
不妨从基环树下手,考虑先连两个叶子节点。
Step 1
那么让我们先证明一个结论:存在叶子节点 x,y,连接 (x,y) 后构成的基环树有偶数个支链。
所谓支链,就是基环树环上的点向外连边的个数。
证明过程(反证法):
假设所有连边方案中,基环树都有奇数个支链。那么对于画出这样的图:
(那些歪歪曲曲的代表其他支链)
那么我们现在断开 (x,y),将 y(x 也行,这里取一个来证明)与一个支链的末端叶节点相连。
那么可以发现 y 处于一个新的环中(下图青色)。
根据假设,这个环应该拥有奇数个支链。
但实际上我们开始假设时,是对任意图的,所以不一定在这条链上有偶数个支链,产生矛盾,假设不成立。
所以,**存在叶子节点 $x,y$,连接 $(x,y)$ 后构成的基环树有偶数个支链**。
## Step 2
我们将对这个拥有偶数条支链的基环树做一些处理。
以下面这个图为例:
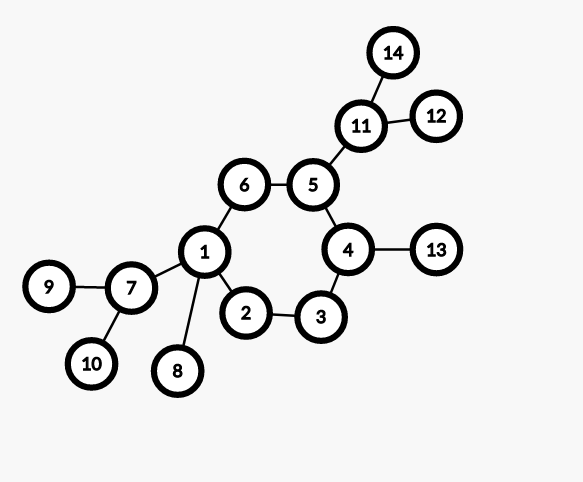
我们将不同支链上的叶子节点两两配对,直到无法配对为止。
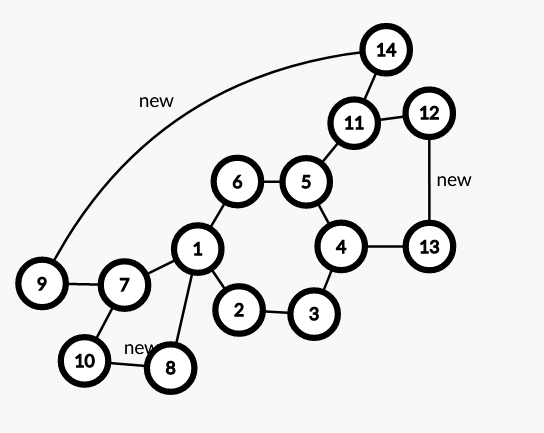
可以看到,这上面每两个点都有至少两条分离路径。
但是这是运气好的情况,假如运气不好,出现这样的情况呢:
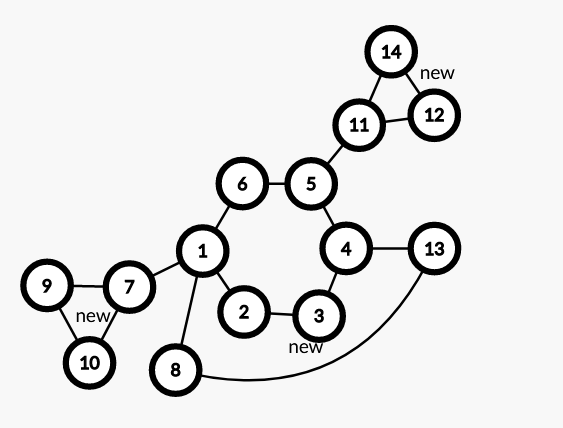
$(9,10)$ 和 $(12,14)$ 连了之后,是无法满足条件的。
症结就在于它们的 $lca$ 不在环上,所以这种情况**是绝对不可以出现的**!
但是运气很差,这种情况就是出现了。那么接下来我们要证明的就是,**这种情况是可以改变成一个合法的解的**。
以下图为例:
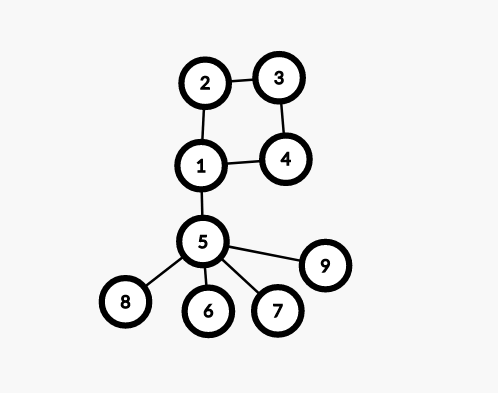
方便起见,我省去了所有已经配对的链,简化为一个环。
可以证明,这些遗留下来的叶子节点一共有偶数个(因为本来有偶数个,两两配对,不能配对到最后肯定剩偶数个)。
并且这个环上面一定有两个叶子节点(毕竟环就是这样构造出来的),我们姑且设为 $3,4$。
断开 $(3,4)$,连接 $(3,8),(4,9)$,得到:
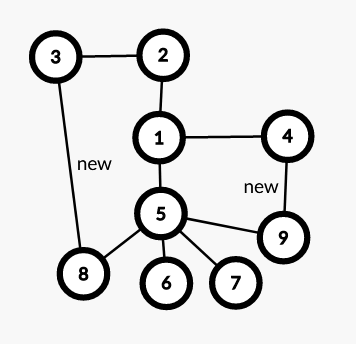
这时候连接 $(6,7)$,就满足条件了:
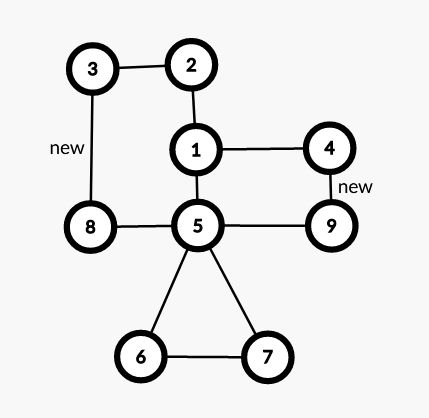
可以见得,遇到这种情况,我们**断开环上的叶子节点,将其与两个未配对的叶子节点相连,构成一个新的大环**。
此时剩余的叶子节点的 $lca$ 就在环上了。
当然这是一种情况,还有其他情况,比如:
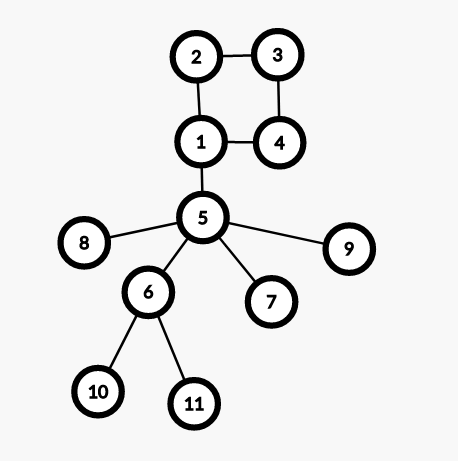
证明方法类似,不再赘述。
这样,每个叶子节点都只与一个叶子节点相连,所以总共 $\dfrac{s}{2}$ 个新增的边。
那么接下来,奇数就好办了,只要新增的这个节点与已经成体系的“大环”上一点相连,就满足条件。
因此奇数时答案为 $\dfrac{s+1}{2}$。
综合两者,得出答案为 $\lfloor\dfrac{s+1}{2}\rfloor$。完结撒花!
~~这估计是这个题第一篇完整证明了这个结论的题解吧~~