```cpp
3
dec 1
new 2
ifneq 1 3 goto 1
```
### task 2
${n\choose 2}=1+2+\dots+n-1=n+(2+\dots+n-2)$,从 $2$ 循环到 $n-2$ 即可。
```cpp
9
dec 1
dec 1
dec 1
assign 2 1
dec 2
new 3
iftry 2 goto 5
dec 1
ifneq 1 4 goto 4
```
### task 3
$600=n+(600-n)$,很直接的想法是构造出 $600-n$ 次循环,变成相反数变成 $n-600$,$600$ 可以视为 $24\times 25$,循环即可。
```cpp
35
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
assign 3 2
dec 3
dec 4
assign 5 6
dec 5
dec 1
ifneq 5 3 goto 29
ifneq 4 2 goto 27
dec 6
new 8
ifneq 1 6 goto 33
```
### task 4
直接加一即可。
```cpp
1
new 1
```
### task 5
$n^2-1=(n+1)(n-1)=n+(n+1)(n-2)+1$。
```cpp
10
assign 2 1
dec 2
dec 2
new 4
dec 1
assign 3 2
dec 3
new 4
ifneq 3 5 goto 7
iftry 1 goto 5
```
### task 6
$n+2000=n+2\times10\times10\times10$。
```cpp
24
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 2
dec 3
dec 3
dec 4
assign 5 8
dec 5
assign 6 8
dec 6
assign 7 8
dec 7
new 9
ifneq 7 2 goto 19
ifneq 6 2 goto 17
ifneq 5 2 goto 15
ifneq 3 4 goto 13
```
### task 7
考虑倍增。将 $p_1$ 一直减去 $2$ 的幂次,若大于等于 $0$ 则倍增,次数加一。
```cpp
13
assign 2 1
dec 3
dec 3
dec 2
dec 2
new 7
assign 4 3
assign 5 6
dec 5
dec 3
dec 2
ifneq 5 4 goto 9
iftry 2 goto 6
```
### task 8
考虑将 $n$ 一直减 $2$ 直到 $n<0$,那么 $n$ 只会为 $-1, -2$ 其中一种。而我们需要做的是将 $-1$ 的情况加 $1$,$-2$ 的情况加 $2$。用一个初始为 $-1$ 的变量,减 $1$ 并判断是否相等,相等再执行一遍加 $1$ 操作。
```cpp
6
dec 1
dec 1
iftry 1 goto 1
dec 2
new 3
ifeq 1 2 goto 4
```
### task 9
$\gcd(n,n-4)=\gcd(4,n-4)=\gcd(n\bmod4,4)$。
类似 task 8 的方法我们可以对 $n$ 一直减 $4$,但是这里的处理方法有点不同。这里我将 $-4$ 的情况变为 $0$ 的情况,然后有 $0,-1,-2,-3$ 的情况,需要增加的数分别为 $5,2,3,2$。对于任意数先 `new` 两次,然后减 $2$。如果等于 $-4$ 则跳回第二个 `new`,如果等于 $-2$ 跳回第一个 `new`。
```cpp
18
dec 1
dec 1
dec 1
dec 1
assign 2 1
dec 2
iftry 2 goto 1
dec 3
dec 3
assign 4 3
dec 4
dec 4
new 5
new 5
dec 1
dec 1
ifeq 1 4 goto 14
ifeq 1 3 goto 13
```
### task 10
这里我用了点~~奇淫技巧~~。思路是尽可能的构造一个一次函数,使得满足条件。然后玩弄半天后发现 $y=4.3x$ 最佳,~~似乎没有更好的了~~。下面是函数图像:
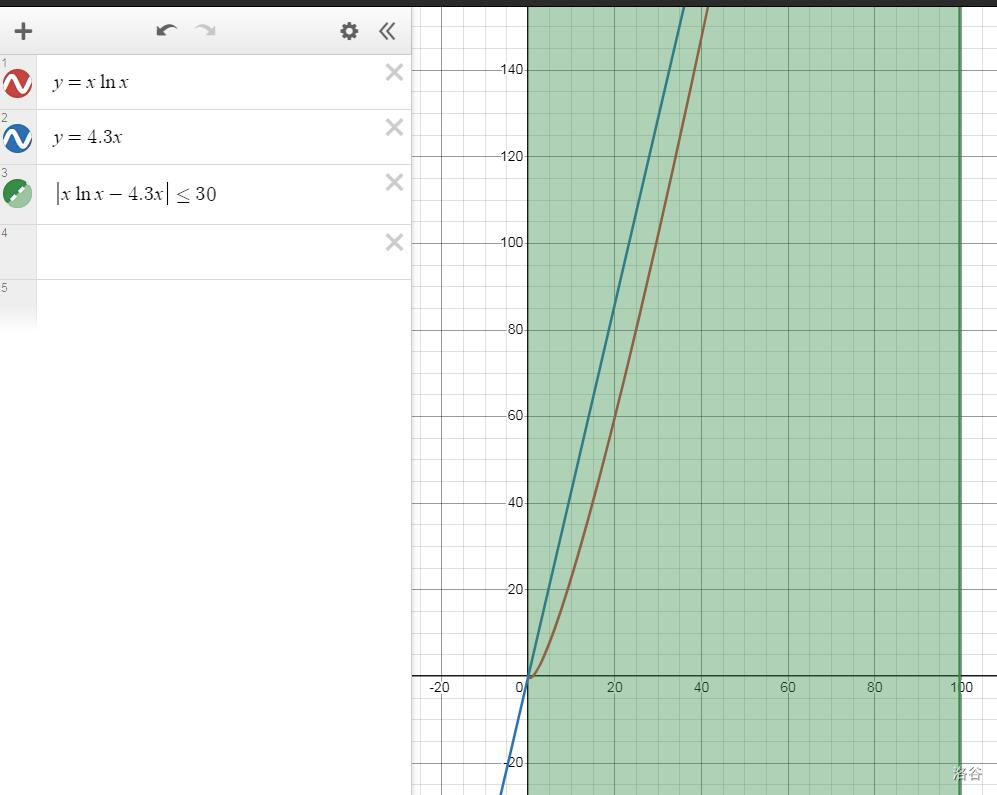
然后如何凑出 $4.3n$ 呢?$4n$ 部分好搞,而 $0.3n$ 部分则可以看成 $\dfrac{n}{3}$,这个只需长度为 $n$,步长为 $3$ 的循环即可,那么就解决了。
```cpp
11
assign 2 1
dec 1
new 4
new 4
new 4
ifneq 1 3 goto 2
dec 2
dec 2
dec 2
new 4
iftry 2 goto 7
```