题解 【第五届传智杯 决赛】
kkksc03
·
2023-04-05 10:56:50
·
个人记录
A 时效「月岩笠的诅咒」
题解
注意到题目所求等价于询问 a,b 的小数点部分是否相同。这里提供三个常见思路:
直接以浮点数形式读入 a,b ,比较其小数部分,即比较 a-\lfloor a\rfloor 和 b-\lfloor b\rfloor 是否相同。然而由于题设输入数据精确到了小数点后 12 位,且整数部分的范围也较大,因此这样做会爆精度。
以字符串来处理。即分别读入两个字符串,比较其小数点后面的部分是否相同。
以长整型来处理。直接读入小数点后面的部分比较就行。
代码
版本 1 :
#include<bits/stdc++.h>
using namespace std;
string a, b;
int main(){
cin >> a >> b;
int u = a.find('.');
int v = b.find('.');
puts(a.substr(u) == b.substr(v) ? "YES" : "NO");
return 0;
}版本 2 :
#include<bits/stdc++.h>
using namespace std;
typedef long long i64;
int main(){
i64 a1, a2, b1, b2;
scanf("%lld.%lld", &a1, &a2);
scanf("%lld.%lld", &b1, &b2);
puts(a2 == b2 ? "YES" : "NO");
return 0;
}B 不死「火鸟 −凤翼天翔−」
题解
容易发现,从 (x_0,y_0) 出发,走了奇偶两步后,能到达的位置只有:
因此考虑以 2 为步距。按照一共走的步数是奇数步还是偶数步来讨论。
在一共走了偶数步的情况下,题目转化为每步可以沿着 x 轴或者 y 轴方向走 2 个单位长度。那么此时 (x_0,y_0) 走到 (x, y) 的最少步数显然是 \dfrac{|x_0-x|}{2}+\dfrac{|y_0-y|}{2} ,在 x_0-x 或者 y_0-y 是奇数的情况下无解。
在一共走了奇数步的情况下,考虑最后一步(奇数步)是怎么走的。把这一步扣除则回到了走偶数步的情况。
代码
#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647 - 1;
int qread(){
int w=1,c,ret;
while((c = getchar()) > '9' || c < '0') w = (c == '-' ? -1 : 1); ret = c - '0';
while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0';
return ret * w;
}
int dis(int a1, int b1, int a2, int b2){
int dx = abs(a2 - a1);
int dy = abs(b2 - b1);
if(dx % 2 == 1 || dy % 2 == 1) return INF;
return dx + dy;
}
int main(){
int a1 = qread(), b1 = qread();
int a2 = qread(), b2 = qread();
int ans = INF;
ans = min(ans, dis(a1, b1, a2, b2));
ans = min(ans, 1 + dis(a1, b1, a2 - 1, b2 - 1));
ans = min(ans, 1 + dis(a1, b1, a2 + 1, b2 + 1));
printf("%d\n", ans >= INF ? -1 : ans);
return 0;
}C 藤原「灭罪寺院伤」
题解
容易发现沿着竖直方向移动与沿着水平方向移动,是可以独立考虑的。最终的答案就是沿着竖直方向移动的最小步数加上沿着水平方向移动的最小步数。
在这两个方向上,问题都可以转化为:
有 n 个区间 [a_i,b_i] 互相嵌套。每次可以将一个区间 [a,b] 变为 [a-1,b-1] 或者 [a+1,b+1] ,但是要时刻保持嵌套状态。现在要将 [a_n,b_n] 变成 [a_{\mathrm{end}},b_{\mathrm{end}}] ,问最小步数。
容易发现,
若 [a_{\mathrm{end}},b_{\mathrm{end}}]\subseteq [a_i,b_i] 则 [a_i,b_i] 不需要移动;
若 a_{\mathrm{end}}\le a_i 则至少要向左移动 a_i-a_{\mathrm{end}} 距离;
若 b_{\mathrm{end}}\ge b_i 则至少要向右移动 b_{\mathrm{end}}-b_i 距离。
并且容易构造出这样一个最优方案。
代码
#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647;
const int MAXN= 1e5 + 3;
int n, xe, ye, X1[MAXN], Y1[MAXN], X2[MAXN], Y2[MAXN];
i64 solve(int e, int *P1, int *P2){
i64 ret = 0;
up(1, n, i){
if(e <= P1[i]) ret += P1[i] - e;
if(e >= P2[i]) ret += e - P2[i];
}
return ret;
}
int qread(){
int w=1,c,ret;
while((c = getchar()) > '9' || c < '0') w = (c == '-' ? -1 : 1); ret = c - '0';
while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0';
return ret * w;
}
int main(){
n = qread(), xe = qread(), ye = qread();
up(1, n, i){
X1[i] = qread(), X2[i] = X1[i] + i - 1;
Y2[i] = qread(), Y1[i] = Y2[i] - i + 1;
}
i64 ans = solve(xe, X1, X2) + solve(ye, Y1, Y2);
printf("%lld\n", ans);
return 0;
}D 不死「徐福时空」
题解
按照题设模拟即可,没有太大难度。
代码
#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647;
const int MAXN= 1e5 + 3;
const int MAXM= 100 + 3;
int ans = 0;
void insert_sort(int n, int *A){
for(int i = 0;i < n;++ i){
int p = i, a = A[i];
for(int j = i - 1;j >= 0;-- j) if(A[j] > A[i]) -- p; else break;
for(int j = i ;j > p;-- j) A[j] = A[j - 1];
A[p] = a, ans += i - p + 1;
}
}
void shell_sort(int n, int m, int *A, int *M){
int *B = new int[n];
for(int j = 0;j < m;++ j){
int l = M[j];
for(int i = 0;i < l;++ i){
int m = 0;
for(int j = i;j < n;j += l) B[m ++] = A[j];
insert_sort(m, B), m = 0;
for(int j = i;j < n;j += l) A[j] = B[m ++];
}
}
}
int n, m, P[MAXN], Q[MAXM];
int main(){
cin >> n >> m;
for(int i = 0;i < n;++ i) cin >> P[i];
for(int i = 0;i < m;++ i) cin >> Q[i];
shell_sort(n, m, P, Q);
cout << ans << endl;
for(int i = 0;i < n;++ i) cout << P[i] << " \n"[i == n - 1];
return 0;
}E 灭罪「正直者之死」
题解
可以证明,在数列 [a_1,a_2,\cdots ,a_p] 满足 u\le a_i\le v 的情况下(u<0<v ),可以通过改变求和的顺序使得计算过程中零时变量始终在 [u,v] 范围内,充要条件即为 u\le \sum a_i\le v 。
必要性显然。下面证明充分性。
假定当前零时变量的值为 x ,剩下来的还没有加到 x 里面的数字,按照它们与 0 的大小关系可以分为两类:大于等于 0 的部分和小于 0 的部分。
如果 v\ge x\ge 0 ,假设剩余的元素存在 a<0 ,由 u\le a\le v 则一定有 u\le a<0 ,于是 u\le x+a\le v 。如果不存在 a<0 ,那么把所有剩下来的元素都加到 x 上也肯定不会超过 v ,因为此时 x 的值就等于 \sum a_i ,而由条件这是不超过 v 的;
如果 u\le x< 0 ,假设剩余的元素存在 a\ge 0 ,由 u\le a\le v 则一定有 0\le a\le v ,于是 u\le x+a\le v 。如果不存在 a\ge 0 ,那么把所有剩下来的元素都加到 x 上也肯定不会小于 u ,因为此时 x 的值就等于 \sum a_i ,而由条件这是不小于 u 的。
因此题目等价于,选出尽可能多的数字,使得这些数字的和在 [-2^{k-1},2^{k-1}) 内。可以使用背包。
设 f_{i,j} 表示在考虑前 i 个数的情况下,凑出一些元素,这些元素的和为 j ,这些元素个数的最大值。容易得到状态转移方程:
f_{i,j}\gets \max(f_{i-1,j} ,f_{i-1,j-a_i}+1)
值得注意的是,可能存在 j 中途大于 v (或者小于 u )而在最后回到 [u,v] 范围内的情况,因此 j 的范围应当是 [nu,nv] 。当然,有理论证明,一组合法的选数方案内的元素(即这些元素的值域为 [u,v] ,且和的值域也为 [u,v] ),在随机排列 的情况下,这些元素的前缀和的值域的期望是 [u\sqrt n,v\sqrt n] 。因此将整个数列进行若干次随机打乱,并且每次把 j 的值域设定为 [u\sqrt n,v\sqrt n] ,最终有极大概率得到正确结果。
当然在这里数据范围没有考察这一点。写一个平凡的 \mathcal O(n^22^k) 做法即可。
一个更好的做法是,注意到如果某个时刻剩余的数字里同时有正数和负数,那么总是可以根据当前临时变量的值选择符号相反的那个数字,这样肯定是合法的。因此,最终肯定只会剩下正数或者只会剩下负数。
以只剩下正数为例,这时候将所有负数加在一起,贪心地去从小到大尽可能多地选择正数,并且使得最后的和在 $[-2^{k-1},2^{k-1})$ 就行了。这种做法复杂度只有 $\mathcal O(n\log n)$。
### 代码
```cpp
#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647;
const int MAXN= 500 + 3;
const int MAXM= 500 * 256 + 3;
int F[MAXM], n, k, o;
int main(){
scanf("%d%d", &n, &k), o = n * (1 << k - 1);
up(0, 2 * o, i) F[i] = -INF;
F[o] = 0;
up(1, n, i){
int a; scanf("%d", &a);
if(a >= 0) dn(2 * o, 0, j) if(F[j] >= 0)
F[j + a] = max(F[j + a], F[j] + 1);
if(a < 0) up(0, 2 * o, j) if(F[j] >= 0)
F[j + a] = max(F[j + a], F[j] + 1);
}
int ans = 0;
up(- (1 << k - 1), (1 << k - 1) - 1, i)
ans = max(ans, F[i + o]);
printf("%d\n", ans);
return 0;
}
```
## F 虚人「无」
### 题解
下文中我们记 $C_i$ 表示子树 $T_i$ 内所有结点的 $c_i$ 之积,$V_i$ 表示子树 $T_i$ 内所有结点的 $v_i$ 之积,用 $\bar V_i$ 表示子树 $T_i$ 以外的所有结点的 $v_i$ 之积。
答案即为
$$
\sum C_i\times \bar V_{i}
$$
$C_i$ 和 $V_i$ 都可以通过一次 dfs 轻易求出。下面考虑 $\bar V_i$。
注意到由于 $m$ 不一定是质数,所以不能简单地将整棵树的 $v_i$ 乘积 $V_1$ 乘上某棵子树的 $v_i$ 乘积的逆元 $\operatorname{inv} V_i$ 来获得 $\bar V_i$。下面介绍两种思路。
#### 思路 1
一种利用树形 $\mathrm{dp}$ 的思路是,尝试利用前缀乘积来避免除法,以此维护每个子树补集的 $v_i$ 乘积。对于当前处理到的节点 $u$,假定我们已经计算出了 $\bar V_u$。记它的儿子节点分别为 $s_1,s_2,\cdots,s_k$。尝试维护这些节点的 $V_i$ 值的前后缀乘积。
- 计算出 $P_i=\prod_{j\le i} V_{s_{j}}$;
- 计算出 $Q_i=\prod_{j\ge i} V_{s_{j}}$。
容易发现 $\bar V_{s_i}=P_{i-1}\times Q_{i+1}\times \bar V_{u}\times v_u$。于是只需要进行一次 dfs 即可。
#### 思路 2
考虑将整棵树拍平到 dfs 序上。那么每棵子树对应着序列上的一段区间 $[l_i,r_i]$。只需要维护 dfs 序上的前后缀乘积 $P_i,Q_i$,就可以轻易地求出 $\bar V_i=P_{l_i-1}\times Q_{r_i+1}$。
### 代码
```cpp
#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647;
const int MAXN= 3e5 + 3;
vector <int> V[MAXN];
int ans, n, p, A[MAXN], B[MAXN], C[MAXN], X[MAXN], Y[MAXN], S[MAXN];
void dfs1(int u, int f){
S[u] = B[u], X[u] = A[u];
for(auto &v : V[u]) if(v != f){
dfs1(v, u);
X[u] = 1ll * X[u] * X[v] % p;
S[u] = 1ll * S[u] * S[v] % p;
}
}
void dfs2(int u, int f){
static int P[MAXN];
static int Q[MAXN];
static int W[MAXN];
int t = 0, o = 0;
for(auto &v : V[u]) if(v != f) W[t ++] = S[v];
P[0] = W[0], Q[t - 1] = W[t - 1];
up( 1, t, i) P[i] = 1ll * P[i - 1] * W[i] % p;
dn(t - 2, 1, i) Q[i] = 1ll * Q[i + 1] * W[i] % p;
for(auto &v : V[u]) if(v != f){
Y[v] = 1ll * Y[u] * B[u] % p;
if(o > 0) Y[v] = 1ll * Y[v] * P[o - 1] % p;
if(o < t - 1) Y[v] = 1ll * Y[v] * Q[o + 1] % p;
ans = (ans + 1ll * X[v] * Y[v]) % p;
o ++;
}
for(auto &v : V[u]) if(v != f) dfs2(v, u);
}
int qread(){
int w=1,c,ret;
while((c = getchar()) > '9' || c < '0') w = (c == '-' ? -1 : 1); ret = c - '0';
while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0';
return ret * w;
}
int main(){
n = qread(), p = qread();
up(1, n - 1, i){
int u = qread(), v = qread();
V[u].push_back(v);
V[v].push_back(u);
}
up(1, n, i) A[i] = qread();
up(1, n, i) B[i] = qread();
dfs1(1, 0), Y[1] = 1, ans = X[1], dfs2(1, 0);
printf("%d\n", ans);
return 0;
}
```
## G 不灭「不死鸟之尾」
### 题解
考虑第 $i$ 辆车停放的位置对它后面的车的影响。假设第 $i$ 辆车停放后,停放在它左侧的车组成的序列为 $A$,右侧的车组成的序列为 $B$,那么最终整个停车场的模样应该是 $[A,i,B]$。记**停放不包含 $\bm i$ 的车辆**的总代价为 $f([A,i,B])$。容易发现:
- $f([A,B,i])=f([i,A,B])$。这是因为从 $A,B$ 的视角来看,这两种情况留下来的是长度相等的连续段,自然两种方案没有区别;
- $f([A,i,B])\le f([A,B,i])$。这是因为在前一种方案里,停放在 $B$ 里面的车辆时,$B$ 区域左边一定会有 $i$ 号车挡在这里;但是在后一种方案里,$B$ 区域左边不一定有车停放(至少不会更劣)。
接着考虑第 $i$ 辆车停放花费的代价,假设此时 $i$ 车要停进去的这段连续空位的总长度为 $s+1$:
$$
\begin{aligned}
W_i-L_i\times l-R_i\times r&=W_i-L_i\times l-R_i\times (s-l)\cr
&=(W_i-sR_i)-l(L_i-R_i)\cr
&=(W_i-sL_i)-r(R_i-L_i)\cr
\end{aligned}
$$
无论是 $W_i-sR_i$ 还是 $W_i-sL_i$,都是定值。
- 假设 $R_i-L_i> 0$,那么我们就希望 $r$ 取得一个最大值 $s$,也就是停在最左侧,这样对 $i$ 来说花费肯定最小;
- 假设 $L_i-R_i< 0$,那么我们就希望 $l$ 取得一个最大值 $s$,也就是停在最右侧,这样对 $i$ 来说花费肯定最小;
- 如果 $L_i=R_i$,那么 $i$ 车停在那里花费都是一样的。
上文我们已经证明了在 $i$ 车停放在最左侧或者是最右侧的情况下,对于剩下来要停进去的车而言花费总是最小的。现在又说明 $i$ 停在最左侧或者最右侧时对于 $i$ 的花费是最小的。因此,一个最优决策一定是 $i$ 停放在最左侧或者最右侧,具体停在哪侧由 $L_i$ 和 $R_i$ 的大小关系决定。
### 代码
```cpp
#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647;
i64 qread(){
i64 w=1,c,ret;
while((c = getchar()) > '9' || c < '0') w = (c == '-' ? -1 : 1); ret = c - '0';
while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0';
return ret * w;
}
const int MAXN = 1e5 + 3;
i64 n, L[MAXN], R[MAXN], W[MAXN]; i64 ans;
int main(){
n = qread();
up(1, n, i) W[i] = qread();
up(1, n, i) L[i] = qread();
up(1, n, i) R[i] = qread();
up(1, n, i){
i64 w1 = W[i] - 1ll * (n - i) * L[i];
i64 w2 = W[i] - 1ll * (n - i) * R[i];
ans += min(w1, w2);
}
printf("%lld\n", ans);
return 0;
}
```
## H 蓬莱「凯风快晴 −富士火山−」
### 题解
假定原树第 $i$ 层的宽度为 $w_i$,选出的导出子树第 $i$ 层的宽度为 $\hat w_i$。同时设导出子树最下面一层对应着原树的第 $d$ 层。容易发现,这棵导出子树一定会有一个大小上限。这个上限可以通过如下方式计算:
$$
\hat w_i\le \min_{j=i}^d\{w_i\}=m_i
$$
这是显然的。因为题设要求我们满足 $\hat w_{i}\le \hat w_{i+1}$,而 $\hat w_i\le w_i$,那么用这些小于等于号就可以建立出这样一个上界。
下面证明这个上界可以被取得。我们随便选择一个第 $d$ 层的节点,连同它的父亲、父亲的父亲,一直到根节点 $1$,全部加入到导出子树内。这条链显然是符合题设的一个合法方案。
这个时候从第 $d$ 层开始,假如第 $d$ 层选到的节点个数还没有 $m_d$ 个,就说明这一层肯定还有节点没选上。同样地,我们把这个节点连同他的所有的祖先全部都给选上。直到第 $d$ 层选上的节点个数已经到了 $m_d$ 个。
接着考虑第 $d-1$ 层,同样地,按照上述步骤,若这一层选到的节点个数还没有 $m_{d-1}$ 个就随便选一些节点连同他们的祖先加进去。一直这样操作,直到第 $1$ 层。
容易发现按照这样的思路最终每一层选出来的节点个数都不会小于 $m_i$ 个。但是这样合法吗?
- 首先,由于每次我们都是将一个节点一直选到了根节点 $1$,因此这一棵树肯定是连通的。
- 接着继续考虑这样的选点过程。假如一个节点没有选上,那么它的所有儿子节点肯定也没有被选上,在儿子节点选上的情况下它的父亲一定被选了。我们用 $0$ 和 $1$ 分别表示之前这个节点有没有被选上过,如果被选上了那么就会对这一层的 $\hat w_i$ 值造成一个贡献。那么从根节点到节点 $i$ 的这条路径,一定组成了这样一个序列:$[0,0,\cdots,0,1,1,\cdots 1]$。这是单调不增的。若干条单调不增的序列全给叠加到一起,那最后一定也是一个单调不增的序列,因此这样的构造方法一定保证了 $\hat w_i\le \hat w_{i+1}$。
因此我们要做的事情就是从 $m$ 序列里选出来一个单调不减的子串,并且最大化这个子串内的元素之和。容易使用单调栈实现。
### 代码
```cpp
#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647;
const int MAXN= 5e5 + 3;
int H[MAXN], V[MAXN * 2], N[MAXN * 2], t;
void add(int u, int v){
V[++ t] = v, N[t] = H[u], H[u] = t;
}
int D[MAXN], W[MAXN], d;
void dfs(int u, int f){
D[u] = D[f] + 1, d = max(d, D[u]), W[D[u]] ++;
for(int i = H[u], v;i;i = N[i]) if((v = V[i]) != f){
dfs(v, u);
}
}
int n, s, ans;
int qread(){
int w=1,c,ret;
while((c = getchar()) > '9' || c < '0') w = (c == '-' ? -1 : 1); ret = c - '0';
while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0';
return ret * w;
}
int main(){
n = qread();
up(1, n - 1, i){
int u = qread(), v = qread();
add(u, v), add(v, u);
}
dfs(1, 0);
using pii = pair<int, int>; stack<pii> S;
int f = 0;
up(1, d, i){
int p = 0;
while(!S.empty() && S.top().first >= W[i]){
s -= S.top().second * (S.top().first - W[i]);
p += S.top().second, S.pop();
}
S.push(make_pair(W[i], p + 1)), s += W[i];
if(s > ans) f = i;
ans = max(ans, s);
}
printf("%d\n", ans);
return 0;
}
```
## I 「不死鸟附体」
### 题解
考虑一个由长度为 $l_0$ 的循环节 $S_0$ 生成的长度为 $l$ 的字符串 $S$:
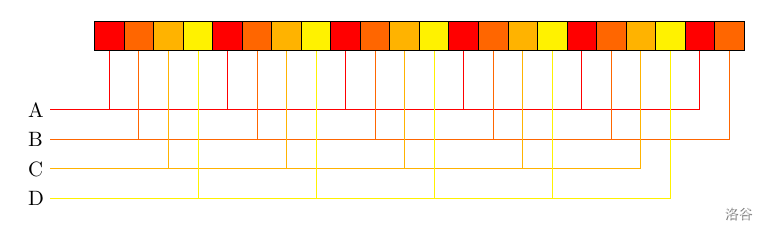
将下标对 $l_0$ 取模来进行分类,容易发现余数相同的下标位置它对应的字符肯定是相同的。这个是「$S_0$ 是 $S$ 的循环节」的充要条件。
我们希望找到一个 $l_0$,使得一个长度为 $l_0$ 的字符串 $S_0$ 为 $S$ 的循环节。那么我们可以贪心地选取 $S_0$ 的每一位为它在 $S$ 里对应的字符里,出现次数最多的那一个字符(容易发现,这样可以使得生成的 $S'$ 与 $S$ 的差值尽量小)。我们需要保证生成的字符串 $S'$ 和 $S$ 的差值不超过 $m$。
为了检查 $l_0$ 是否符合条件,一个容易想到的想法是去利用刚刚得到的充要条件进行校验。我们去枚举每一对**应该相同**的字符对,判断它们在 $S$ 里是不是真的相同。直觉告诉我们,如果不相同的情况发生得很少,那么生成的 $S'$ 应该和 $S$ 的差值很小。由于字符对的数量极多,直接全部枚举肯定会超时,因此可以**抽样**。随机抽查一些应该相同的字符对,检验它们是否相等。
但是不相同的情况数发生多少次以下,这个 $S'$ 才是可以被接受的呢?这就需要我们进行定量分析。
由于下标按照取模后的结果分成了不同的类,我们可以取出其中某一类来进行观察:
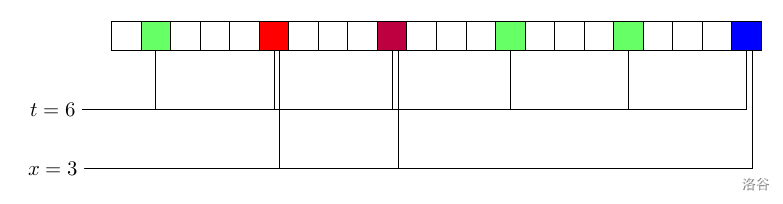
在这一类中,一共有 $t$ 个字符。出现次数最多的字符出现了 $t-x=3$ 次,而剩下来的 $x=3$ 个字符不等于这个出现次数最多的字符。如果我们在这个类里随机抽查一个点对(为了方便代码的编写,这里抽查的方式是,随机生成 $i\in\{0, 1, 2, \cdots ,t-1\}$,$j\in\{0, 1, 2, \cdots, t - 1\}$,那么 $(i,j)$ 就是生成的一组合法点对),点对不相等的概率是多少?
容易发现一共可以找到 $t^2$ 组合法点对。这 $t^2$ 组点对可以分成三类:
- 两个字符全都都是出现次数最多的字符;
- 两个字符有一个是出现次数最多的字符;
- 两个字符全都不是出现次数最多的字符。
第一种情况点对一定相等,第二种情况一定不等,第三种情况可能相等也可能不相等。三种情况出现的次数分别是 $(t-x)^2,2x(t-x),x^2$,容易得到点对不相等的概率的范围:
$$
\dfrac{2x(t-x)}{t^2}\le p\le \dfrac{2x(t-x)+x^2}{t^2}
$$
我们等概率抽查每一类下标。假设一共有 $u$ 类下标。记第 $i$ 类下标里,不等于出现次数最多的那个字符的下标的个数为 $x_i$,那么总的抽查到不相等点对的概率的取值范围是:
$$
\sum_{i=1}^u\dfrac{1}{u}\times \dfrac{2x_i(t-x_i)}{t^2}\le p\le \sum_{i=1}^u\dfrac{1}{u}\times \dfrac{2x_i(t-x_i)+x_i^2}{t^2}
$$
容易发现 $u=l_0$,$t\approx \dfrac{l}{l_0}$。但是 $x_i$ 的值是变量,我们希望找到 $p$ 的确切的上下界。
首先可以约定一下 $x$ 的范围。
- 由于题设保证了 $S$ 是一个 $S_0$ 无限循环生成后,修改了不超过 $n$ 个位置得到的,所以**必然存在一个 $\bm{l_0}$** 使得 $\sum x_i\le n$;
- 由于题设只要我们求出一个与 $S$ 相差不超过 $m$ 的字符串 $S'$,所以一个**不可以**接受的字符串,一定有 $\sum x_i> m$。
我们需要计算出在 $\sum x_i\le n$ 的情况下,$p$ 的**最大值**;同时需要计算出 $\sum x_i> m$ 的情况下,$p$ 的**最小值**。
事实上,无论是 $f(x)=2x(t-x)$ 还是 $f(x)=2x(t-x)+x^2$,它们都是开口向下的抛物线,全都是**下凸函数**。可以证明在 $x_i$ 最平均(也就是 $x_i=\dfrac{n}{u}$)的情况下 $\sum f(x_i)$ 取得最大值,在 $x_i$ 最不平均(也就是 $\dfrac{m}{t/2}$ 个 $x_i$ 满足 $x_i=t/2$,其他的 $x_i=0$)的情况下 $\sum f(x_i)$ 取得最小值。
可以使用导数相关知识进行证明,限于篇幅这里不再展开。
应用上述结论,可以得到:
$$
\begin{aligned}
p&\le \sum_{i=1}^u\dfrac{1}{u}\times \dfrac{2x_i(t-x_i)+x_i^2}{t^2}\cr
&=\sum_{i=1}^{l_0}(2x_i(\dfrac{l}{l_0}-x)+x_i^2)\times \dfrac{1}{l_0}\times \dfrac{l_0^2}{l^2}\cr
&\le l_0\times \dfrac{2nl-n^2}{l_0^2}\times \dfrac{1}{l_0}\times \dfrac{l_0^2}{l^2}\cr
&=\dfrac{2nl-n^2}{l^2}
\end{aligned}
$$
此为 $\sum x_i\le n$ 的情况下 $p$ 的最大值。代入题设条件 $n=3\times 10^3$,$l=3\times 10^5$,可以得到最大值约为 $\dfrac{1}{50}$。
$$
\begin{aligned}
p&\ge \sum_{i=1}^u\dfrac{1}{u}\times \dfrac{2x_i(t-x_i)}{t^2} \cr
&=\sum_{i=1}^{l_0}(2x_i(\dfrac{l}{l_0}-x_i))\times \dfrac{1}{l_0}\times \dfrac{l_0^2}{l^2}\cr
&\ge m\times \dfrac{2l_0}{l} \times 2\times \dfrac{1}{2}\times \dfrac{l}{l_0}\times \dfrac{1}{2}\times \dfrac{l}{l_0}\times \dfrac{1}{l_0}\times \dfrac{l_0^2}{l^2}\cr
&=\dfrac{m}{l}
\end{aligned}
$$
此为 $\sum x_i\ge m$ 的情况下 $p$ 的最小值。代入题设条件 $m=10^4$,$l=3\times 10^5$,可以得到最小值约为 $\dfrac{1}{30}$。
也就是说,如果一个 $S_0$ 是不合法的,那么对应的 $p$ 值不可能会小于 $\dfrac{1}{30}$;我们总是可以找到一个 $p$ 值不大于 $\dfrac{1}{50}$ 的 $l_0$,那么找到的这个 $l_0$ 一定是合法的。
实践上,我们可以随机抽查 $h=100$ 组字母对,用蒙特卡洛的方式计算出 $p$ 的值。取使得 $p$ 值最小的 $l_0$,那么它一定是符合条件的。
### 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
const int INF = 2147483647;
const int MAXN= 3e5 + 3;
const int MAXM= 26 + 3;
int n, m, lmax, l, h = 100, l0, ans = INF; char S[MAXN]; mt19937 MT;
int main(){
scanf("%d%d%d%d", &l, &lmax, &n, &m);
scanf("%s", S);
for(int i = lmax;i >= max(1, lmax / 2);-- i){
int cnt = 0;
for(int j = 1;j <= h;++ j){
int p = MT() % i, q = (l - 1 - p) / i;
int x = p + MT() % q * i;
int y = p + MT() % q * i;
cnt += S[x] != S[y];
}
if(cnt <= ans) l0 = i, ans = cnt;
}
printf("%d\n", l0);
for(int i = 0;i < l0;++ i){
map <char, int> M; char f = 'a';
for(int j = i;j < l;j += l0)
if((++ M[S[j]]) >= M[f]) f = S[j];
putchar(f);
}
return 0;
}
```
## J 「蓬莱人形」
### 题解
统计 $[l, r]$ 内符合条件的 $a_i$ 的个数,显然可以转化成统计 $[1, r]$ 内符合条件的个数减去 $[1, l - 1]$ 内符合条件的个数。又因为题目可以离线,所以可以扫描线,每次加入第 $i$ 个数,然后处理询问区间为 $[1, i]$ 的询问。
我们需要统计满足 $(a+x)\bmod m<(a+y)\bmod m$ 的 $a$ 的个数。为了方便进行讨论,可以先取 $a_0=a\bmod m$,$x_0=x\bmod m$,$y_0=y\bmod m$。接着讨论 $x_0,y_0$ 的相对大小:
- **第一种情况 $\bm{x_0=y_0}$**,此时一定不存在符合条件的 $a$。询问的结果就是 $0$。
- **第二种情况 $\bm{x_0<y_0}$**,此时又可以分成两种情况:
- $a_0+y_0< m$ 时一定有 $a_0+x_0<a_0+y_0$;
- $a_0+x_0\ge m$ 时一定有 $a_0+y_0\ge m$,所以各减去 $m$ 后一定有 $a_0+x_0< a_0+y_0$。
- 对于其他情况一定不符合条件。所以一定有 $m-x_0\le a_0$ 或者 $a_0\le m-y_0 - 1$。
- **第三种情况 $\bm{x_0>y_0}$**,容易发现当且仅当 $a_0+x_0\ge m$ 且 $a_0+y_0<m$ 时符合条件。即 $m-x_0\le a_0\le m-y_0-1$。
值得注意的是,第二种情况可以通过简单地从所有情况里减去不符合条件的 $a$ 的个数。所以也可以转化为统计 $m-y_0\le a_0\le m-x_0-1$ 的 $a_0$ 的个数。那么两种情况都可以转化成统计在一定区间内的 $x_0$ 的个数。不妨把该区间记为 $[l_0,r_0]$。容易发现,$[l_0,r_0]$ 的长度不超过 $m$。
此时我们可以对询问给出的 $m$ 进行根号分治。也就是确定一个常数 $b$,分别讨论 $m\le b$ 和 $m> b$ 的情况。
#### 情形一:$\bm{m\le b}
这部分的 m 只有 b 个。此时我们可以在加入一个新的 a 之后暴力地维护每个 m 的答案。具体而言,我们对每个 m 都开一个桶,即用 C[m,i] 存储模 m 后余 i 的 a 的个数。每次加入一个新的 a 后,枚举 m 的值,让 C[m,a\bmod m] 的值增加 1 。对于每个查询操作 [l_0,r_0] ,直接暴力地查询 C[m,l_0\sim r_0] 这部分元素之和即可。
容易发现时间复杂度为 \mathcal O(nb+qb) ,空间复杂度为 \mathcal O(b^2) 。
情形二:\bm{m> b}
这部分的 m 较多,[l_0,r_0] 的长度也比较大,不便于直接维护 C[m,i] 的值。但是此时 \left\lfloor\dfrac{a}{m}\right\rfloor 的值不太大,可以去考虑统计 [l_0+im,r_0+im],\ i=0,1,2,\cdots,\left\lfloor\dfrac{v}{m}\right\rfloor 内的 a 的值有多少个。我们在值域上使用数据结构进行统计。
我们一共会在值域上插入 n 个数字,查询次数最多一共有 q\left\lfloor\dfrac{v}{b}\right\rfloor 次,所以我们希望找到一个查询效率高,但是修改效率可以低一些的数据结构。于是考虑分块,块长为 t 。我们在每个块内维护前缀和,以及维护以块为单位的另一个前缀和。每次插入一个数字 a ,需要花费 \mathcal O(t+v/t) 的效率来更新这些前缀和,但是查询时可以 \mathcal O(1) 地回答每个询问。取 t=\sqrt v 时效率最高。
容易发现在取 b=\sqrt v 的情况下,可以得到一个优秀的时间复杂度 \mathcal O(q\sqrt v) 。
代码
#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647;
const int MAXN= 1e5 + 3;
const int MAXQ= 5e5 + 3;
const int BLOK= 1200 + 1;
const int MAXM= MAXN / BLOK + 3;
int C[BLOK + 3][BLOK + 3], v = 100000, b = v / BLOK;
int L[MAXQ], R[MAXQ], X[MAXQ], Y[MAXQ], M[MAXQ], T[MAXQ], A[MAXN];
int P[MAXN], Q[MAXN], S[MAXM];
int qread(){
int w=1,c,ret;
while((c = getchar()) > '9' || c < '0') w = (c == '-' ? -1 : 1); ret = c - '0';
while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0';
return ret * w;
}
vector <int> O[MAXN];
int main(){
int n = qread(), z = qread();
up(1, n, i) A[i] = qread();
up(1, z, i){
L[i] = qread(), R[i] = qread();
X[i] = qread(), Y[i] = qread(), M[i] = qread();
O[L[i] - 1].push_back(-i);
O[R[i] ].push_back( i);
}
up(1, n, i){
int a = A[i], t = a / BLOK;
{
up(1, BLOK, j) C[j][a % j] ++;
int l = t * BLOK;
int r = min(v, t * BLOK + BLOK - 1);
up(a, r, j) P[j] ++;
up(t, b, j) Q[j] ++;
}
for(auto &o : O[i]){
int d = abs(o), f = o > 0 ? 1 : -1;
int m = M[d], x0, y0, w = 0;
int x = X[d] % m;
int y = Y[d] % m;
if(x == y) continue;
if(x < y){
x0 = m - y, y0 = m - x - 1, T[d] += i * f, f *= -1;
} else {
x0 = m - x, y0 = m - y - 1;
}
if(x0 > y0) continue;
if(m <= BLOK){
up(x0, y0, j) w += C[m][j];
} else {
for(int l = x0, r = y0;l <= v;l += m, r += m){
r = min(r, v);
int p = l / BLOK;
int q = r / BLOK;
if(p == q){
w += P[r];
if(l % BLOK != 0) w -= P[l - 1];
} else {
w += P[r] + Q[q - 1];
if(l % BLOK != 0) w -= P[l - 1];
if(p != 0) w -= Q[p - 1];
}
}
}
T[d] += f * w;
}
}
up(1, z, i)
printf("%d\n", T[i]);
return 0;
}