P2753题解
Grisses
·
·
题解
题面
如果做本题时,你知道 皮克定理,那么会非常轻松,如果不知道,现在就会知道了。
皮克定理:
皮克定理是用来计算点阵中顶点在格点上的多边形面积的,公式表示为 S=a+\dfrac{b}{2}-1,其中 a 表示多边形内部的点数,b 表示多边形落在格点边界上的点数,S 表示多边形的面积。
皮克定理的适用条件又:
$$p+\gcd(n,m)+\gcd(|n-p|,m)$$
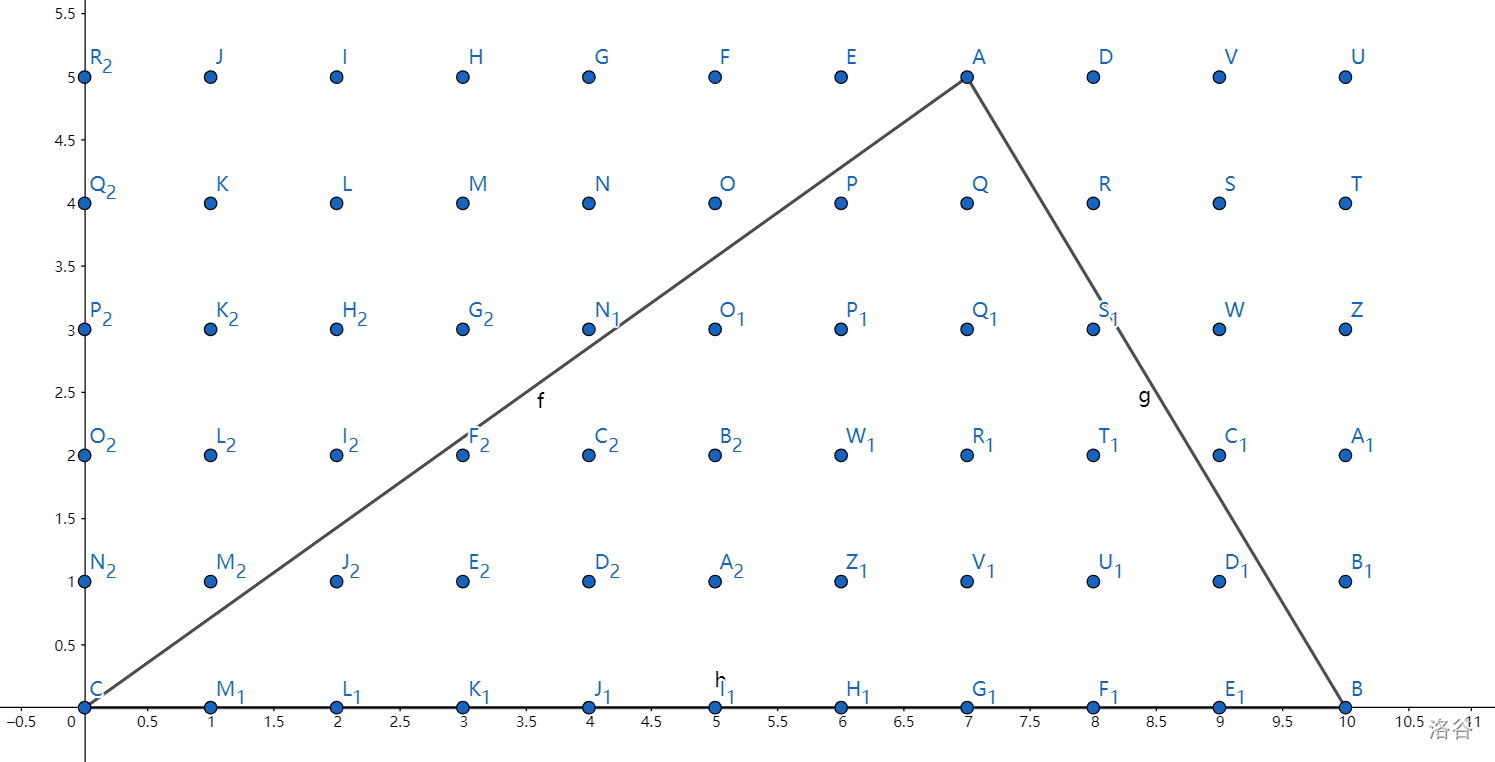
$p+1$ 是 BC 边上的格点数,$\gcd(n,m)+1$ 是 AC 边上的格点数(看经过了几个最小矩形),$\gcd(|n-p|,m)+1$ 是 AB 边上的格点数(同理)。最后,因为三个顶点被多算了一次,减掉 3。
最后三角形内的格点数 $a$ 就是 $S-\dfrac{b}{2}+1$ 了。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m,p,B;//B是边上的格点数
double P,a,b,S;//P是半周长,S是面积
double len(int x1,int y1,int x2,int y2){return sqrt(1.0*(x1-x2)*(x1-x2)+1.0*(y1-y2)*(y1-y2));}//求距离
int main()
{
scanf("%d%d%d",&n,&m,&p);
a=len(0,0,n,m);
b=len(p,0,n,m);
P=(a+b+p)/2.0;
S=sqrt(P*(P-a)*(P-b)*(P-p));//海伦公式
B=p+__gcd(n,m)+__gcd(abs(n-p),m);//上面讲过
printf("%d",int(S+1-B/2.0+0.5));//反推a
return 0;
}
```