题解:P3375 【模板】KMP
Zilljy258
·
·
题解
模式串和模板串我分不大清楚,但我们暂且记短串叫做模式串吧。
这个算法大概就是用来判断能否在主串中匹配到子串。
KMP 算法在入门阶段是一个很常考的字符串算法,后期高级阶段不知道还考不考,因为我菜。
下面就来讲一讲思想:
一、最长公共前后缀
这里提到了最长公共前后缀的概念。
什么是最长公共前后缀?
前缀:字符串中不包含最后一个字符,必须包含第一个字符的连续子串。
后缀:字符串中不包含第一个字符,必须包含最后一个字符的连续子串。
那么一个字符串的最长公共前后缀,就是这个串中长度最长的一对相同的前缀和后缀。
举个例子:
abcab
ababab
abcba
它们的最长公共前后缀分别是:
ab
abab
a
注意两个点:
- 前缀和后缀可以重叠,但是都不可以等于原串。
- 不要自己想象着就把后缀倒过来!公共前后缀不是回文串。
二、失配数组
失配数组顾名思义就是在匹配失败的时候用到的数组。
我们记为 fail 数组。
呃,好像有点绕,多读几遍理解一下。
所以 $fail$ 数组存的是最长公共前后缀的长度。
有什么用呢,当模式串和主串匹配失败的时候,我们需要跳到模式串的最长公共前后缀去继续匹配,这就是该数组在匹配失败时的作用。
这里后面会详细讲到,看不懂别着急,理解 $fail$ 的含义就好了。
## 三、算法流程
在程序的开始,我们遍历主串,同时与模式串进行匹配。
(不得不拿出经典套图了!)
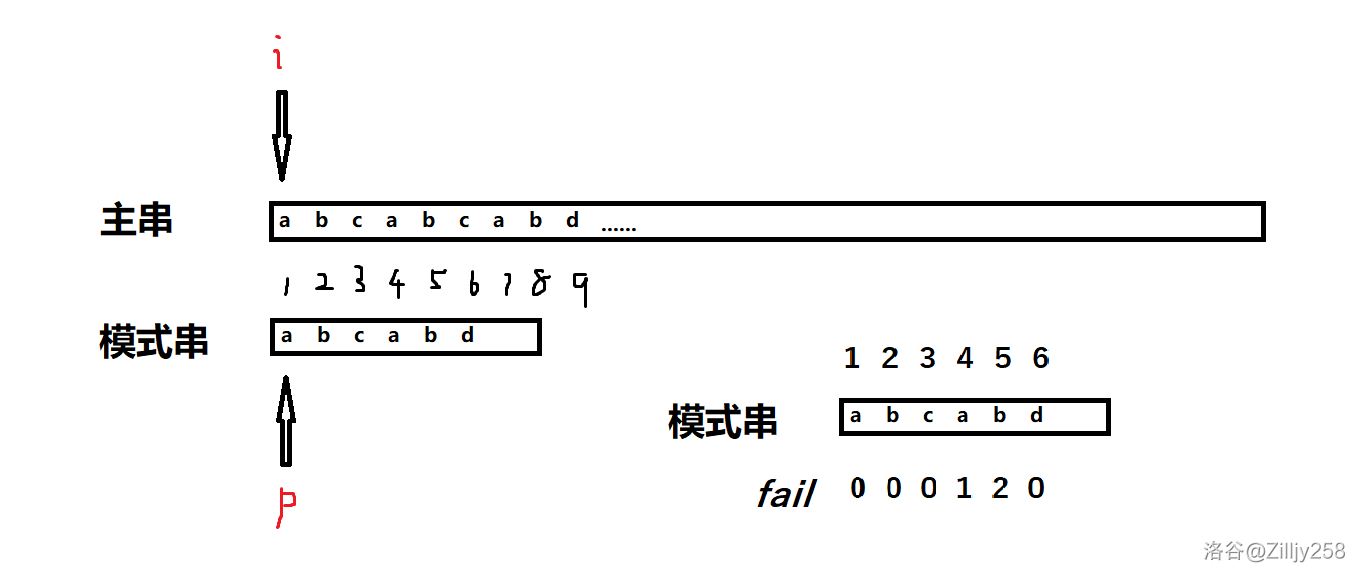
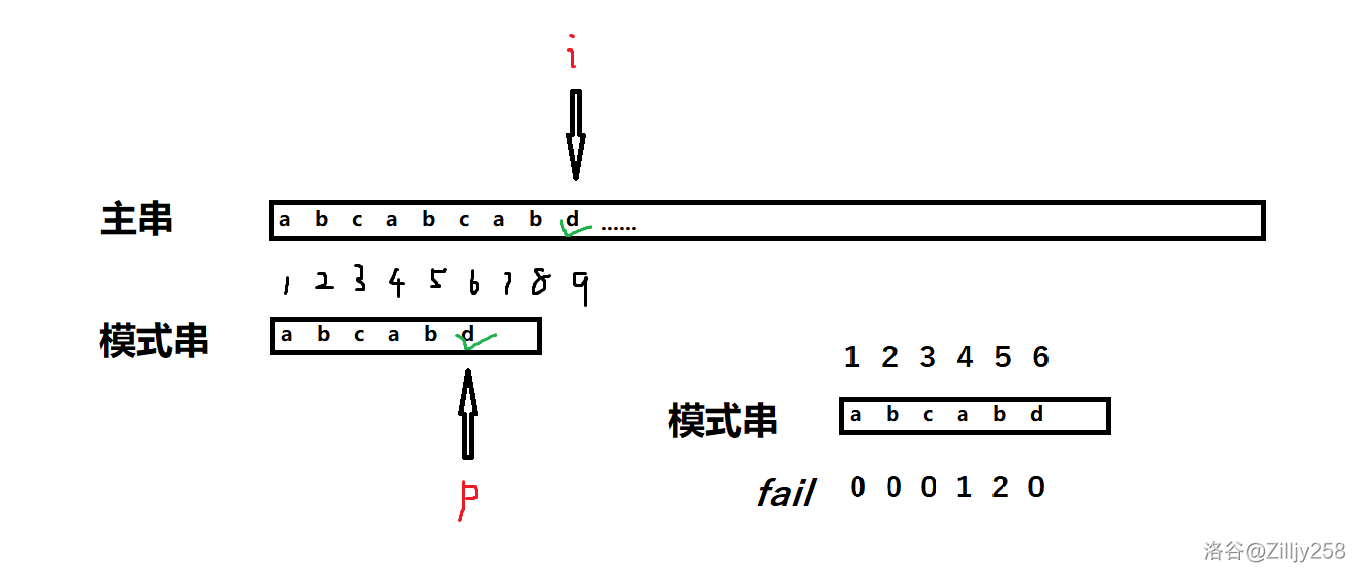
$i$ 是遍历主串的变量,$p$ 是我们模式串的指针。
起初,匹配很平稳(两个指针共同向右移动)……直到:
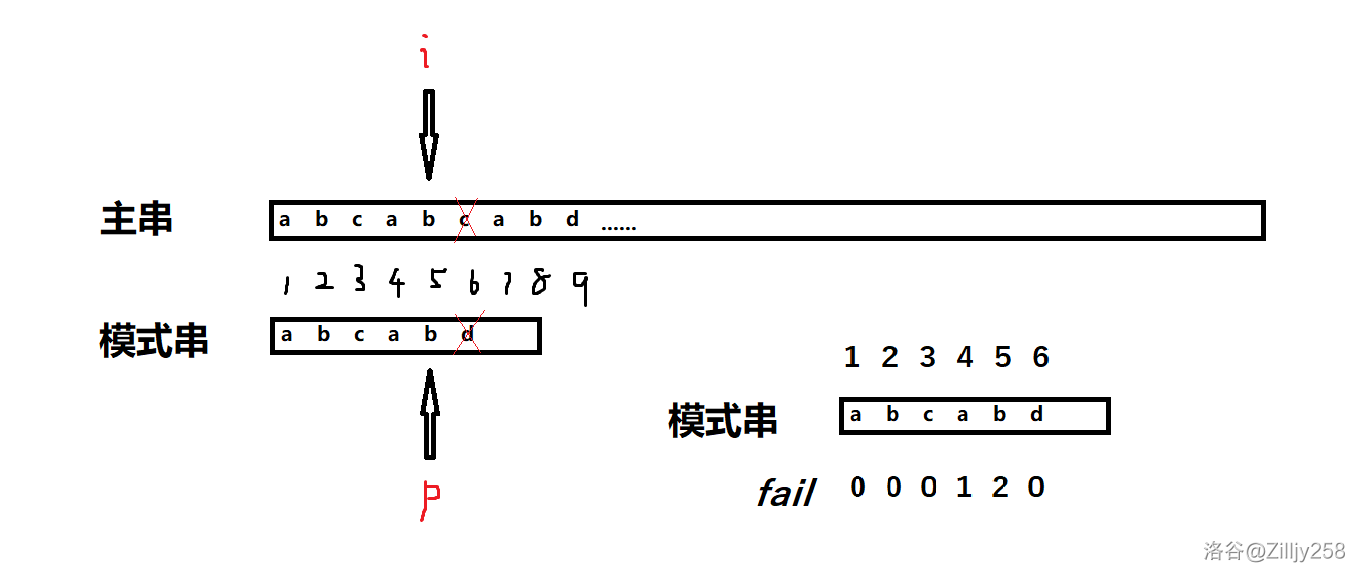
接下来这一位(画红叉号的位置)不一样!
此时,匹配失败!我们跳转至模式串 $fail_p$ 继续匹配。
### 为啥要跳 $fail_p$?
因为如果此时我们暴力退回去重新从零开始匹配实在是太慢了。
在我们失配之前,模式串和主串还是可以正常匹配的。仅仅是这一位不匹配了。从模式串的头重新开始岂不是前功尽弃了?
聪明的科学家们想到:既然之前都可以匹配,那之前的子串的**所有公共前后缀一定也可以匹配!**
如下图,三个绿色的串是完全相等的!
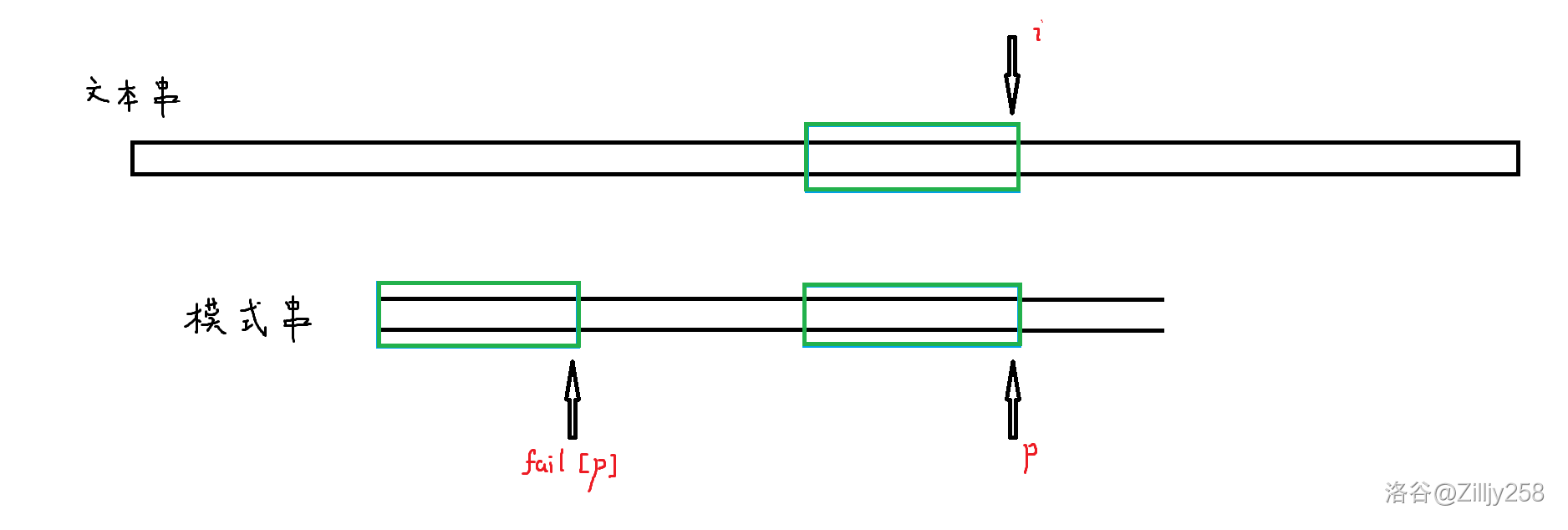
查表可知,$fail_5$ 值为 $2$,那我们跳呗!
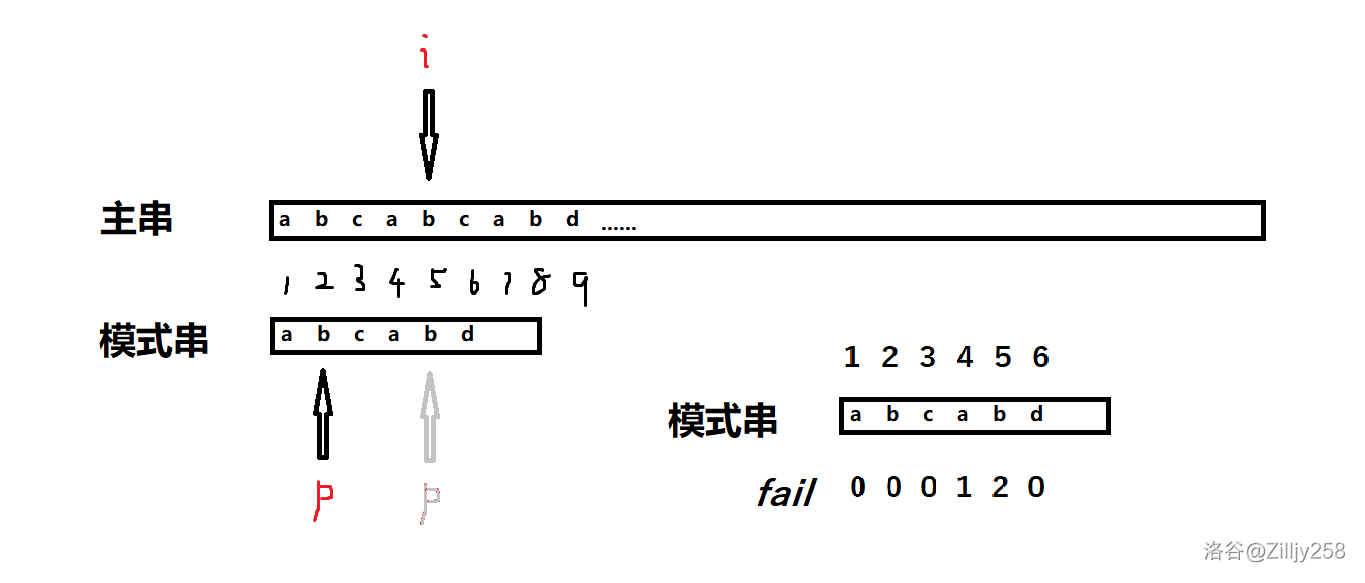
好的,跳完我们发现模式串的前两位和主串中$i$ 前面的两位果然是一样的。(都为“ab”)
可以继续进行下一位匹配了。(如果下一位还不匹配,就再调 $fail_2$,一直到跳到可以匹配或者 $p$ 归零)
继续匹配……直到结尾,$p=6$ 模式串跑完了。
这时候我们知道:匹配成功!
---
代码放一下。
```cpp
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char s[1000010];
char t[1000010];
int fail[1000010];
int main(){
scanf("%s%s",s+1,t+1);
int n=strlen(s+1);
int m=strlen(t+1);
int p;
fail[0]=0;
p=0;
for(int i=1;i<m;++i){ //这里在求 fail 数组。
while(t[p+1]!=t[i+1]&&p) p=fail[p]; //失配就跳 fail。
if(t[p+1]==t[i+1]){ //下一位可以匹配,我们就前进一位。
p++;
}
fail[i+1]=p;
}
p=0;
for(int i=1;i<=n;++i){ //这里在进行文本串和模式串的匹配。
while(t[p+1]!=s[i]&&p) p=fail[p]; //失配就跳 fail。
if(t[p+1]==s[i]){
p++;
}
if(p==m){ //匹配成功!
printf("%d\n",i-m+1);
p=fail[p];
//这里注意一下,匹配成功以后也要跳 fail,具体原理和失配一样,都是前后缀相同嘛。
//不过如果题目要求匹配的模式串不能重叠,这里就得 p=0 了。好像有个剪布条的题就得这么写。
}
}
for(int i=1;i<=m;++i){
printf("%d ",fail[i]);
}
return 0;
}
```
写模板题的题解就是累,还写不明白。欸。
---
### Update:
2025.4.6:@[Frielen](https://www.luogu.com.cn/user/1125685) 提醒我更正了一个错误的例子,感谢!
2025.7.21:@[jiangjiangQwQ](https://www.luogu.com.cn/user/590609) 提醒我更正了一处错别字,感谢!