P5419 [CTSC2016]单调上升序列 题解
KAMIYA_KINA
·
·
题解
Tag
构造。
Description
你需要构造一个 n 阶完全图,使得其最大上升路径长度最小。
## Solution
非常好玩的构造题,看了鱼大的题解之后又学到了新知识呢!
先给出题面中的一个证明,对于一个带权无向完全图而言,一共有 $2n$ 个点,其有 $n(2n-1)$ 条边,每个点上放一个人,然后将边从小枚举到大,每次交换两个点上的人,那么所有人一共走了 $2n(2n-1)$ 步,所以一个人就走了 $(2n-1)$ 步,然后这 $(2n-1)$ 步就是答案的下界了。
现在的问题是我们需要构造一个完全图来达到这个下界,接下来的内容大多是鱼大的方法给的启发。
考虑一个完全图的生成子图 $H$ 是 $k-$正则的,即为这个生成子图中所有点的度数为 $k$,那么我们称这个生成子图 $H$ 是 $G$ 的一个 **$k-$因子**。
特殊地,$G$ 的一个 $1-$因子就是这个图的一个**完美匹配**。(根据定义即可证明)
那么给出一个非常显然的结论:**偶数阶完全图 $K_{2n}$ 一定存在 $1-$因子分解**。
而且一个 $1-$因子一定是只有 $n$ 条边,那么这个完全图 $K_{2n}$ 一定可以分解成 $2n-1$ 个 $1-$因子。(因为他有 $n(2n-1)$ 条边嘛)
我们惊讶的发现这个东西的数值跟答案的下界一样,所以我们就可以想办法去构造这 $2n-1$ 个 $1-$因子,然后保证这 $2n-1$ 个因子中第 $i$ 个当中的值严格小于第 $i+1$ 个就可以了。
思考这样为什么是对的,根据 $1-$因子的定义,这个生成子图中点度数为 $1$,所以通过了一条第 $i$ 个 $1-$因子的边后,不可能再次达到第 $i$ 个 $1-$因子的点,这是显然的,所以只能往更高的 $1-$因子转移,但是整体的 $1-$因子个数是 $2n-1$ 个,所以肯定不会上升超过 $2n-1$ 次,证毕。
接下来思考如果构造。
我们将这 $2n$ 个点分成两部分,第一部分是 $2n-1$ 个正多边形围在最外圈,最后一个点放在里面,之后就可可以~~螺旋构造~~很容易构造了。每个 $1-$因子就是将中间这个点连到周围的 $2n-1$ 个点其中一个上,然后其他的点与中心点连的这条边垂直就可以了,具体可以看下图,是 $n=4$ 时的一种构造:
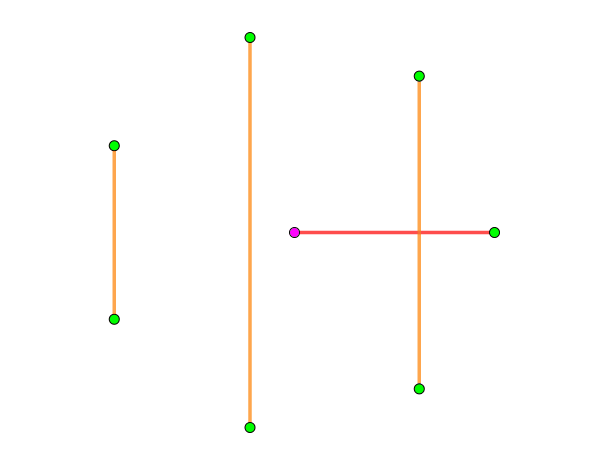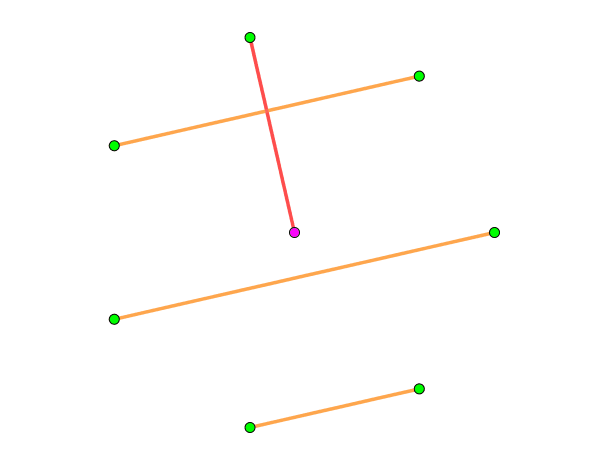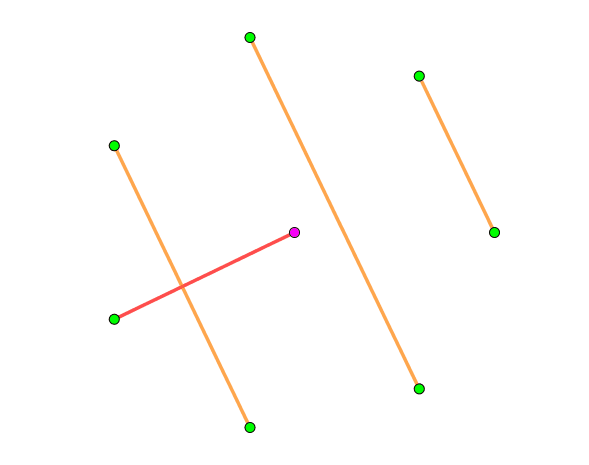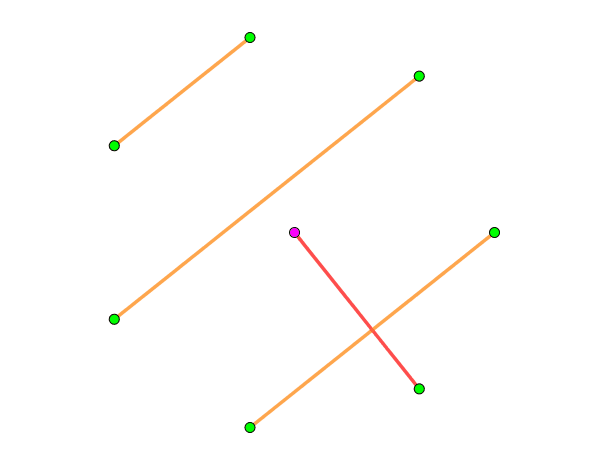
(从鱼大那里蒯的,图床崩了的话可以点一下去[原地址](https://yhx-12243.github.io/OI-transit/records/uploads/12.gif)看)
然后直接做就可以了。
时间复杂度 $O(n^2)$.
## Code
```cpp
const int N = 5e2 + 1;
int g[N][N];
inline void solve() {
int n = rd - 1, w = 0;//钦定第 n 个点为放到中间的那个点
for(int i = 0; i < n; i++) {
g[i][n] = g[n][i] = ++w;
for(int j = 1; j <= n >> 1; j++) {//螺旋构造转转转
int u = (i - j + n) % n, v = (i + j) % n;
g[u][v] = g[v][u] = ++w;
}
}
for(int i = 0; i < n; i++)
for(int j = i + 1; j <= n; j++)
cout << g[i][j] << (j == n ? '\n' : ' ');
return ;
}
```
## Final
本来是想要做另一道题来着,然后看到鱼大的题解里面放了这一题的链接,以为是前置知识什么的,发现那题比这题简单多了。