P8010 「Wdsr-3」令人感伤的红雨
I_am_Accepted
·
·
题解
Preface
赛场上一开始打的暴力,O(n\log^2n) 的线段树 + 二分拿了 70 pts,没想到 100 pts 代码只写了这么点(如下 Code,没压行)。
不过还是给这个 D 题和出题人 @八云蓝 好评。
Analysis
线段树 + 二分就不讲了。反正读者人均 AK 月赛水平
下文将 \alpha(n)(反阿克曼函数)看作常数处理。
不要被题目中的 A(l,r),B(l,r),\Omega(l,r) 吓到,题目中的 A(l,r) 翻译成人话就是数组中区间 [l,r] 内的最大值位置,相同的取靠右的。
其实认真推导一下,\Omega(l,r)=\max(0,|l-A(1,r)|),接下来问题就在维护 A(1,x) 上了。
本白内障 OIer 漏看的条件:y\in[0,10^9]。
就是说修改操作只有前缀加一个非负数。
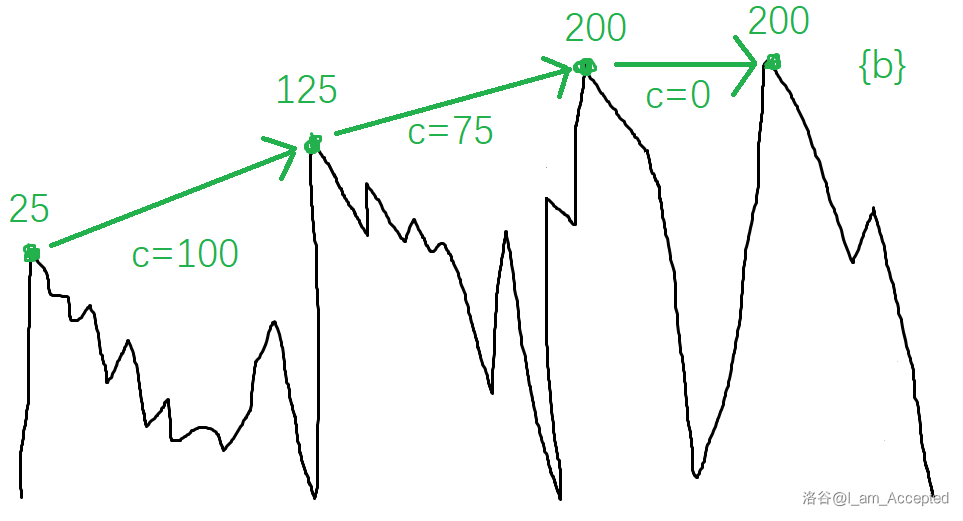
我们将 a_x=\max\limits_{i=1}^x(a_i) 的所有 x 存入 \{b\}。
发现操作只会让 \{b\} 内元素只减不增。
我们尝试均摊 O(n) 吧!
算法(丑图预警):
初始化:
将 f_x 记为小于等于 x 的最大 \{b\} 中的元素。
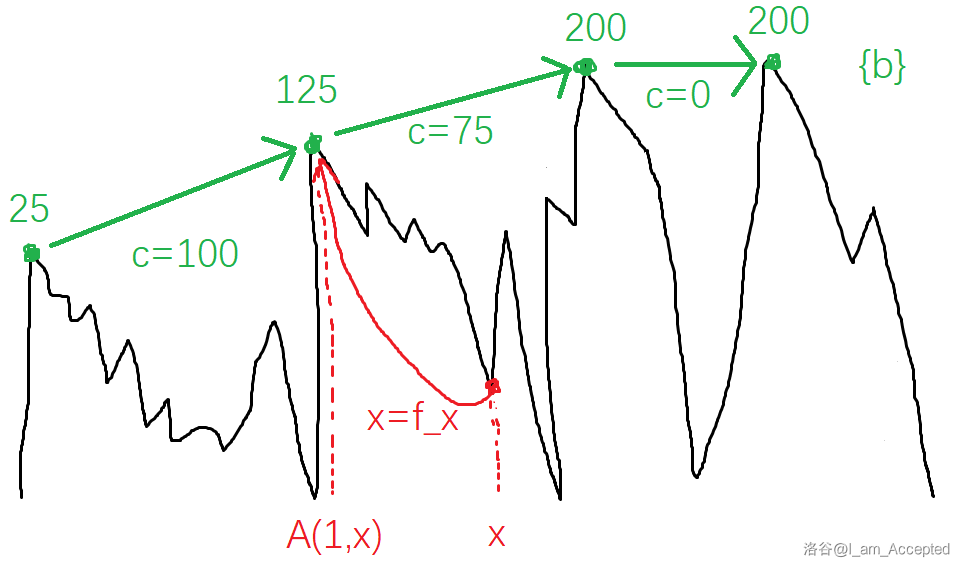
**询问** $A(1,x)$:
类似并查集,将 $x$ 一直跳 $f_x$(可路径压缩),终点即为 $A(1,x)$。
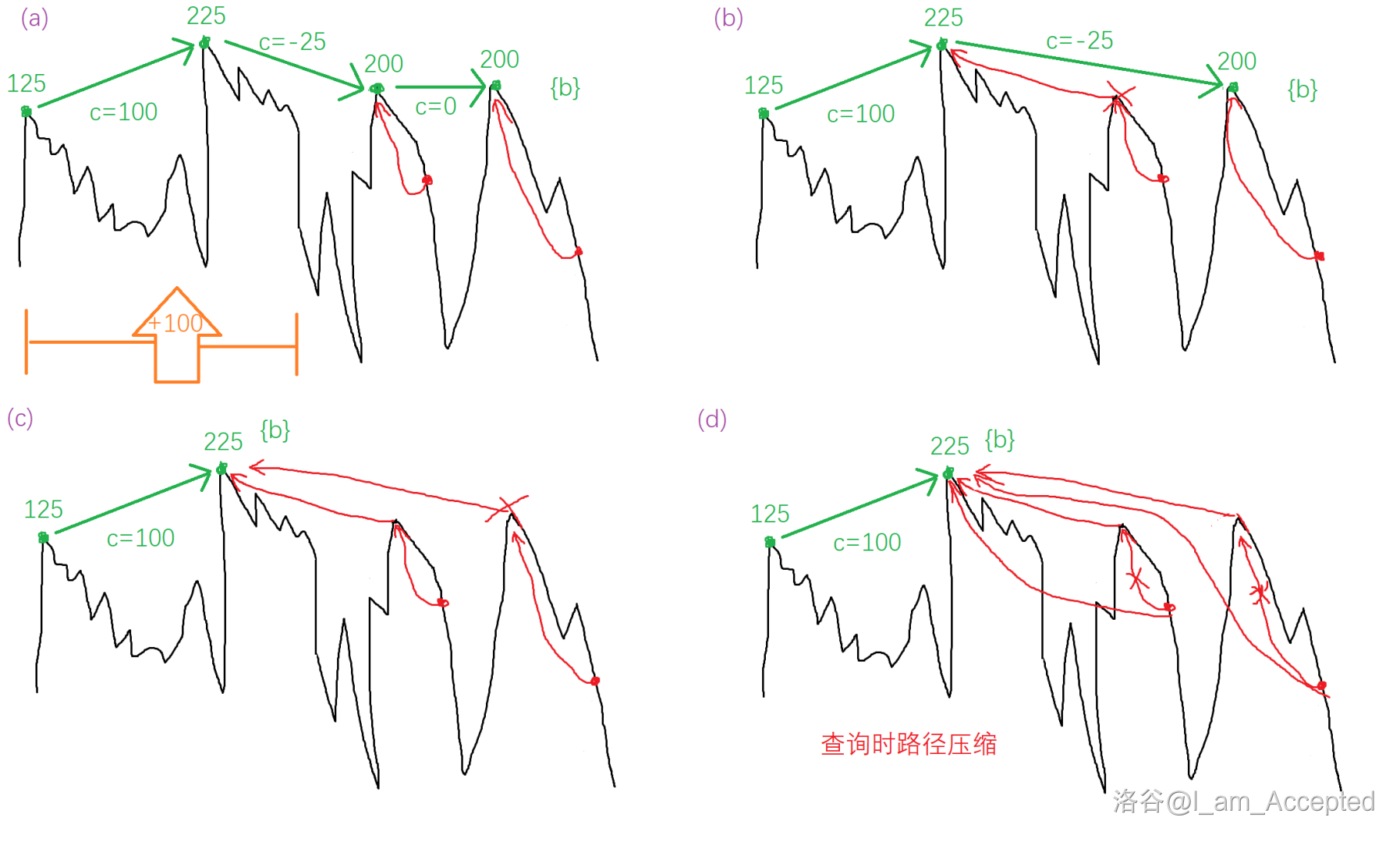
**修改** $[1,x]$ 加上 $y$:
将 $x$ 跳到 $A(1,x)$,将链表中的边权 $-y$,如果边权 $<0$ 将 $A(1,x)$ 链表中的后继从 $\{b\}$ 中删除,重复直至停止。
所以这个算法叫做什么名字呢?~~不知道的话就叫 ZSJ 链表并查集吧(doge)~~
**Upd:**
当然,本蒟蒻的语文非常得垃圾,所以这里写上 @[Konata28](https://www.luogu.com.cn/user/177029) 的语言:
首先,初始的序列肯定有一个单调递增的峰,假设是 $x_1,x_2,x_3,\dots$(即我的 $\{b\}$)。
那么 $[x_{i},x_{i+1})$ 之间的查询的结果都会是 $x_{i}$。
然后我们发现因为是前缀加非负整数,所以 $[x_i,x_{i+1})$ 区间内的查询答案,要么是 $x_i$,要么是因为修改之后的 $x_{i-1}$ 大于 $x_i$ 了导致合并到 $x_{i-1}$ 里面了,$x_{i-2},x_{i-3},\dots$ 同理。
所以我们可以初始化集合,$[x_i,x_{i+1})$ 内的数都在 $x_i$ 的集合内。
如果因为修改导致的 $x_{i-1}>x_i$(即链表边权 $<0$),那么就把 $x_i$ 的集合合并到 $x_{i-1}$ 的中。
## Code
```cpp
#define For(i,j,k) for(register int i=j;i<=k;i++)
#define N 6000100
int n,q,a[N];
int nxt[N],c[N],f[N];
inline int gf(int x){return f[x]==x?x:f[x]=gf(f[x]);}//get father
signed main(){
n=read(),q=read();//fast read
For(i,1,n) a[i]=read();
For(i,1,n) f[i]=i;
For(i,1,n) nxt[i]=n+1;//list
For(i,1,n) c[i]=-1;//the delta(cost) to nxt[i]
int tmp=1;
For(i,2,n){
if(a[i]>=a[tmp]){
nxt[tmp]=i;
c[tmp]=a[i]-a[tmp];
tmp=i;
}else f[i]=tmp;
}
int op,x,y,del;
while(q--){
op=read(),x=read(),y=read();
if(op==1){
tmp=gf(x);
c[tmp]-=y;
while(nxt[tmp]<n+1 && c[tmp]<0){
del=nxt[tmp];//delete it
c[tmp]+=c[del];
nxt[tmp]=nxt[del];
f[del]=tmp;
nxt[del]=n+1;
c[del]=-1;
}
}else write(max(0,x-gf(y))),pc('\n');//fast write
}
return 0;
}
```