数据结构补完计划 P11900~P12000
noip
·
·
个人记录
计划逐步做完所有公开的以数据结构为主的题目,涉及到做法超出目前能力(如高级字符串)的以及难度低(紫以下)的会被跳过。
难度评测分为:下位紫,中位紫,上位紫,下位黑,中位黑,上位黑,彩。
P11901 数组的划分
3min:这才看到数据随机,每次贪心选最长的子区间是最优的,于是可以用弹飞绵羊的套路,LCT 维护后继。由于数据随机,所以每次匹配的长度最多是 O(\log n) 的,可以暴力预处理所有长度 O(\log n) 的初始数组区间的哈希,每次 link cut 的时候花费 O(\log n) 的时间找到具体 link 到哪里。
总时间复杂度 O((n+m+q)\log n)。
难度评测:下位紫(LCT 模板太难)。
P11923 [PA 2025] 砖块收集 / Zbieranie klocków
10min:2\times2 的肯定删不了,然后画各种奇怪图形看看什么样的能删。
15min:2\times2 的是被完全保护的,然后发现只有连接两个被完全保护的区域的折线部分不能删,而且这个折线还必须像围棋的征子一样一直拐弯。
16min:直接对斜率正负的 45 度维护两种线段树,每次修改最多影响 O(1) 个 2\times2 位置的保护性,以及 O(1) 个斜线的保护性,然后在线段树上二分即可。
总时间复杂度 O(k+q\log n)。
难度评测:和数据结构没什么关系,中位紫?
P11930 [PA 2025] 吃树叶 / Liście
之前看过。我 2021 年都出过 3dmq 了,你们 2025 年出 2dmq 是几个意思。
难度评测:下位紫。
P11945 [KTSC 2025] 军事基地 / safezone
之前看过,不过忘了怎么做了。
4min:考虑扫描线优化建图,维护一棵线段树,然后每次就是插入一个区间,要将和这个区间有交的区间全部都连边。
用线段树拆区间之后,用标记永久化讨论结点上下关系的套路,对于新加入的区间,递归过程中经过的 O(\log n) 个结点上的标记都会和这个区间合并。但是实际上我们只需要对一个结点,随便挑一个标记与这个区间合并就行,因为一个结点的多个标记之前已经维护了连通性。
现在的问题就是如何高效删除一个结点的标记,这里因为随便维护任何一个标记就行,所以很简单,可以用链表,或者用对顶堆的思路,维护两个队列,一个是插入队列一个是删除队列,每次删除就往删除队列里面插入元素,然后 while 队列头相同 pop 就行。
然后的问题就是现在只对被插入的标记,考虑了其祖先标记和其的贡献,没有考虑子树内标记的贡献。
这个我们反着做一遍扫描线,子树内的标记就会被该标记更晚打上,就可以计算这部分贡献了。
最后 DFS 一遍图求连通性即可。
总时间复杂度 O(n\log n)。
难度评测:中位紫。
P11947 [KTSC 2025] 可爱区间 / maxsum
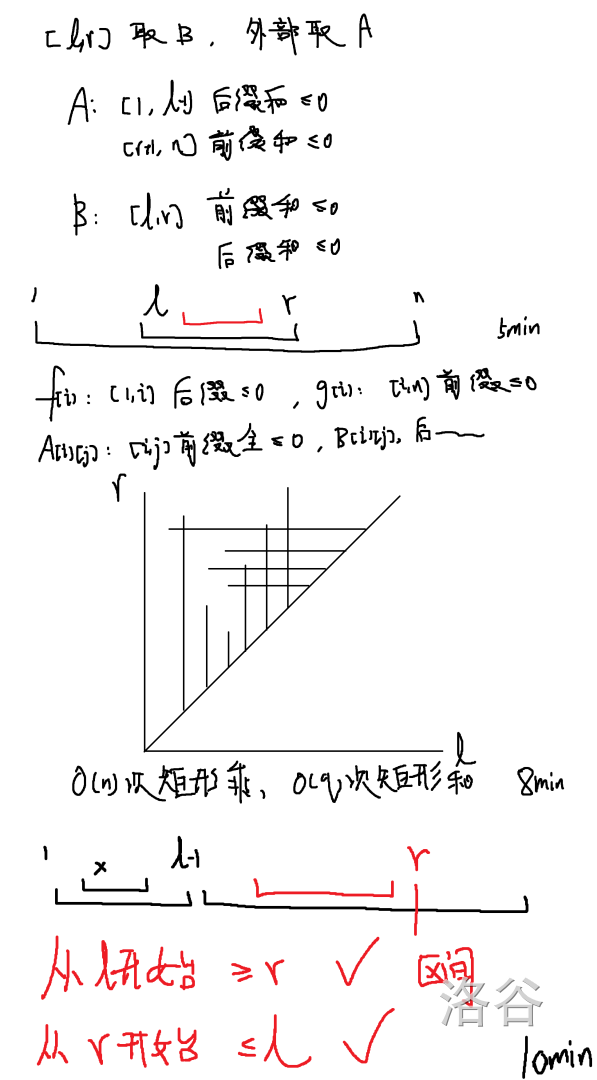
5min:推一下条件:[l,r] 是最大子段和的条件是什么。
-
-
-
-
$3,4$ 可以对每个 $l$ 每个 $r$ 用线段树上二分来处理,对每个 $l,r$,合法的另一个端点一定是一个区间。
10min:刚刚少算了一种情况,还需要:
5. $[l,r]$ 的区间和比 $[1,l-1]$ 的最大子段和大。
6. $[l,r]$ 的区间和比 $[r+1,n]$ 的最大子段和大。
对固定的每个 $l,r$,合法的另一个端点显然也是连续的一个区间。
把每个线段变成补集,于是现在变成有一堆横着竖着的线段,每次询问矩形内有多少位置没有被任何线段覆盖,直接扫描线维护矩形面积并即可。
16min:发现还是做错了一个地方,因为是 $[l,r]$ 的区间和比 $[1,l-1]$ 的最大子段和大,所以实际上是要求值域的一个区间限制,和序列的区间限制没法共存。
继续研究题目性质,发现固定 $l$,只有 $[l,i]$ 构成前缀和 $\max$ 的那些 $i$ 才是合法的,不然违背了前面的一些条件,于是我们维护出 $[l,i]$ 的前缀 $\max$ 单调栈,每次相当于只有某个 $i$ 的区间是符合条件的。
这里虽然我们发现只有单调栈位置是合法的,但是因为同时有 $l$ 和 $r$ 的限制,所以实际上我们还需要放宽限制,不管每个点是否在单调栈上了,因为不在单调栈上的点会被前面的条件排除。于是我们在单调栈数据结构上查出了对固定的 $l$ 来说合法的 $i$ 区间使得 $[l,i]$ 不违背 $5$ 条件,对固定的 $r$ 来说合法的 $i$ 区间使得 $[i,r]$ 不违背 $6$ 条件。
至此所有条件都可以表示为一条横线或者竖线,再套用 10min 的矩形面积并即可。
总时间复杂度 $O((n+q)\log n)$。
难度评测:下位黑。
### P11949 [KTSC 2025] 木筏制作
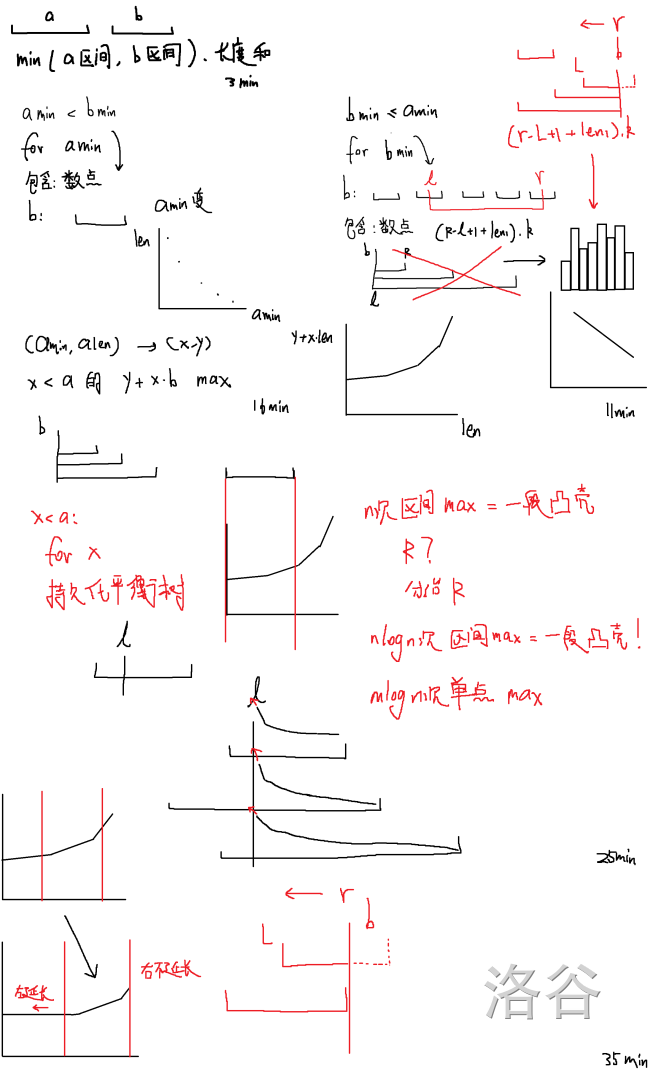
3min:发现题目等价于求从 $a$ 中选一个区间,$b$ 给定的区间中选一个区间,让总的 $\min$ 乘 长度 尽可能大。
考虑讨论一下最小值是哪里取到的。
11min:对于 $\min(b)\le \min(a)$ 的情况比较简单,我们枚举 $b$ 的 $\min$,此时 $b$ 序列会被划分为若干个连续段,每个连续段内是 $\ge$ 当前枚举的 $\min$ 的数。
我们可以根据 $\min(b)$ 的限制判断出在该限制的条件下能选的最优的 $a$ 的区间长度,设为 $len_a$。
每次询问的 $b$ 区间和这些连续段的关系有两种:
1. 包含:这个比较简单。可以发现所有连续段拓展长度只会发生 $O(n)$ 次,当每个连续段拓展长度时,因为我们知道 $len_a$,于是可以算出所有 $b$ 拓展形成的极长区间所对应的最优值,问题变成有 $n$ 个区间,每次询问区间内子区间的 $\max$,可以扫描线做。
2. 在询问区间边界处相交,这个麻烦一些。类似 $1$ 那样预处理出所有 $b$ 内极长的区间,极长的条件是发生拓展则 $\min$ 会变化。我们考虑右端点 $r$ 询问相交的答案,对 $b$ 做扫描线,从右往左扫,扫到一个极长区间,则插入一条直线 $(r-L+1+len_a)\times \min(b)$。每次询问 $[l,r]$ 需要满足 $l\le L$ 该直线才能产生贡献。这里需要注意,$r\ge L$ 是不必要的,因为 $r<L$ 会把 $(r-L+1)$ 算成负数。然后对于 $l\le L$ 的限制可以分治掉,这部分总复杂度是 $O((n+m)\log^2n)$ 的。
16min:对于 $\min(a)<\min(b)$ 的情况比较麻烦。
我们枚举 $\min(a)$,包含的情况还是能数点。具体来说我们找出每个 $\min(a)$ 对应的长度 $len(a)$。对于每个 $b$ 的极长区间,设该区间的最小值是 $\min(b)$,则我们要求 $\min(a)<\min(b)$ 的情况下,所有 $(\min(a),len(a))$ 构成的直线中,固定 $x$ 的 $y$ 最大直线。这里可以将直线排序,依次加入 “李超线段树”中,并查询单点值。找到极长区间后还是要做一遍数点。
为了处理不包含的情况,我们把前面这个“李超线段树”改成一个持久化平衡树,维护出所有历史版本,这样可以在要求 $\min(a)<\min(b)$ 的情况下求出一个区间所对应的 $\max$。
接下来我们用 11min 类似的扫描线过程,对每个 $b$ 的极长区间,对该区间的 $\min(b)$,我们在 $\min(a)<\min(b)$ 的持久化平衡树版本中提取出和该极长区间长度相同的一个区间,这个区间构成一个凸壳。然后将该凸壳做一个加上直线的简单变换,得到将该 $a$ 区间和 $b$ 区间拼起来后的凸壳。
然后将这个凸壳的贡献放到每个 $l$ 的答案序列上,具体来说,就是将该极长区间对拼起来的凸壳取 $\max$。
这里复杂度是 3log 的,因为 $r$ 有一维限制,需要分治掉,$l$ 我们是区间对凸壳取 $\max$,需要分治乘单点对凸壳取 $\max$。两个凸壳取 $\max$ 需要在持久化平衡树上二分,所以还有一个 log。
需要注意这里询问全是单点询问,所以修改全部是标记永久化形式的。
总时间复杂度 $O((n+m)\log^3n)$。
35min:我们考虑通过 11min 的做法来去掉对 $r$ 的分治。
我们刚刚的做法是区间对一个凸壳取 $\max$,现在直接改成全局对一个凸壳取 $\max$,将我们的凸壳做一个斜率为 $0$ 的左延长线。这样每次操作就是一个全局的凸壳对一个只有前缀的凸壳取 $\max$,还是可以用持久化平衡树 $O(\log n)$ 实现。
40min:补全细节。和 critnos 的做法应该是类似的,不过我滥用了持久化平衡树可以随便复制和拼接的特性。类似那个用持久化平衡树做闵可夫斯基和的奇怪东西。
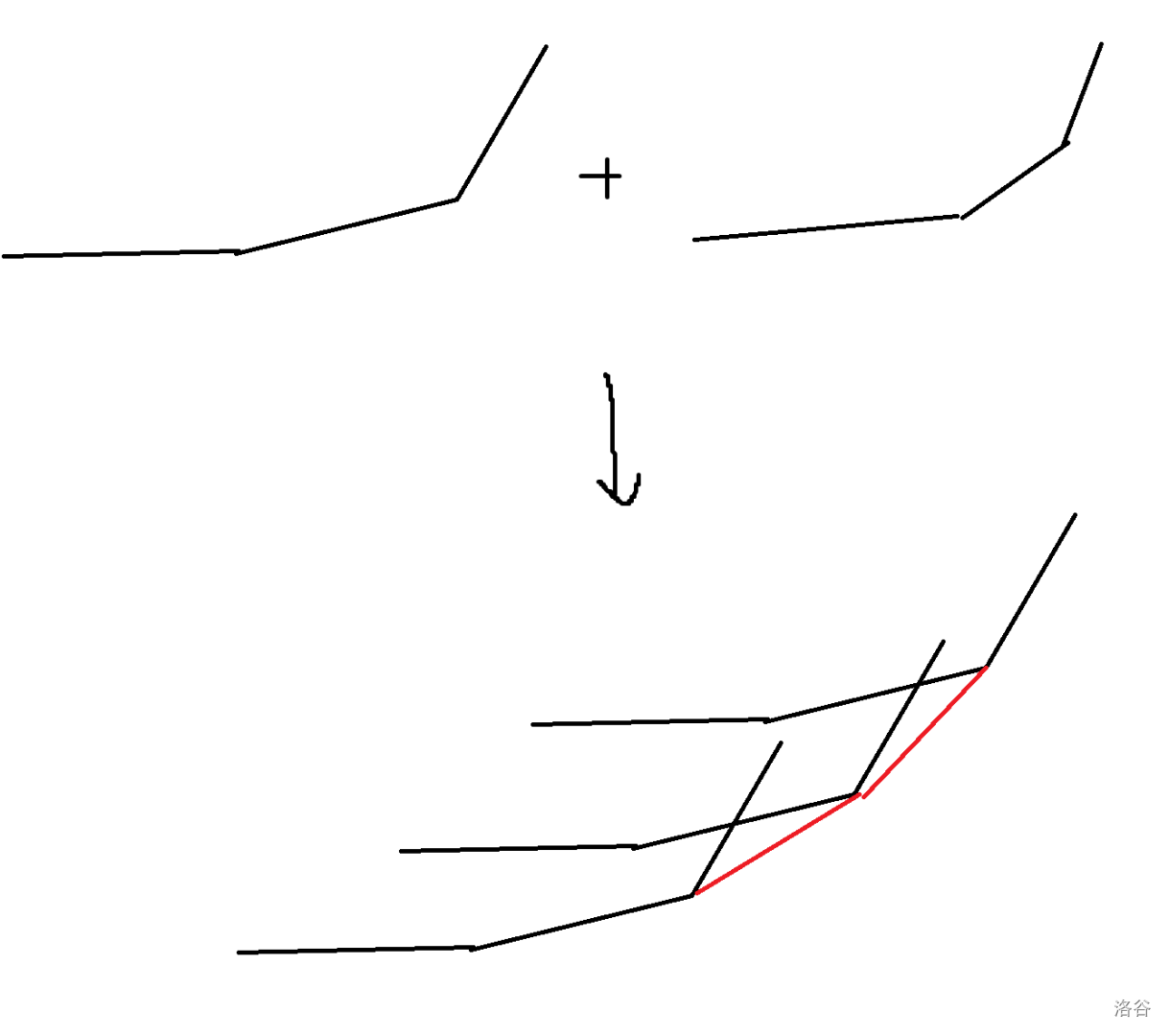
我们对两个凸壳做闵可夫斯基和,直接用持久化平衡树维护其中一个凸壳,对另一个凸壳上的两个点,我们相当于将这个持久化平衡树的凸壳做了两次平移,然后会构成一个新的凸壳,这个凸壳直接用持久化平衡树上二分后分裂合并得到。于是我们可以对另一个凸壳上的每个点都得到一个持久化平衡树的版本,然后将这些版本合并在一起,得到最终的闵可夫斯基和。
总时间复杂度 $O((n+m)\log^2n)$。
难度评测:中位黑(思维难度),上位黑(代码难度)。
### P11956 「ZHQOI R1」树图
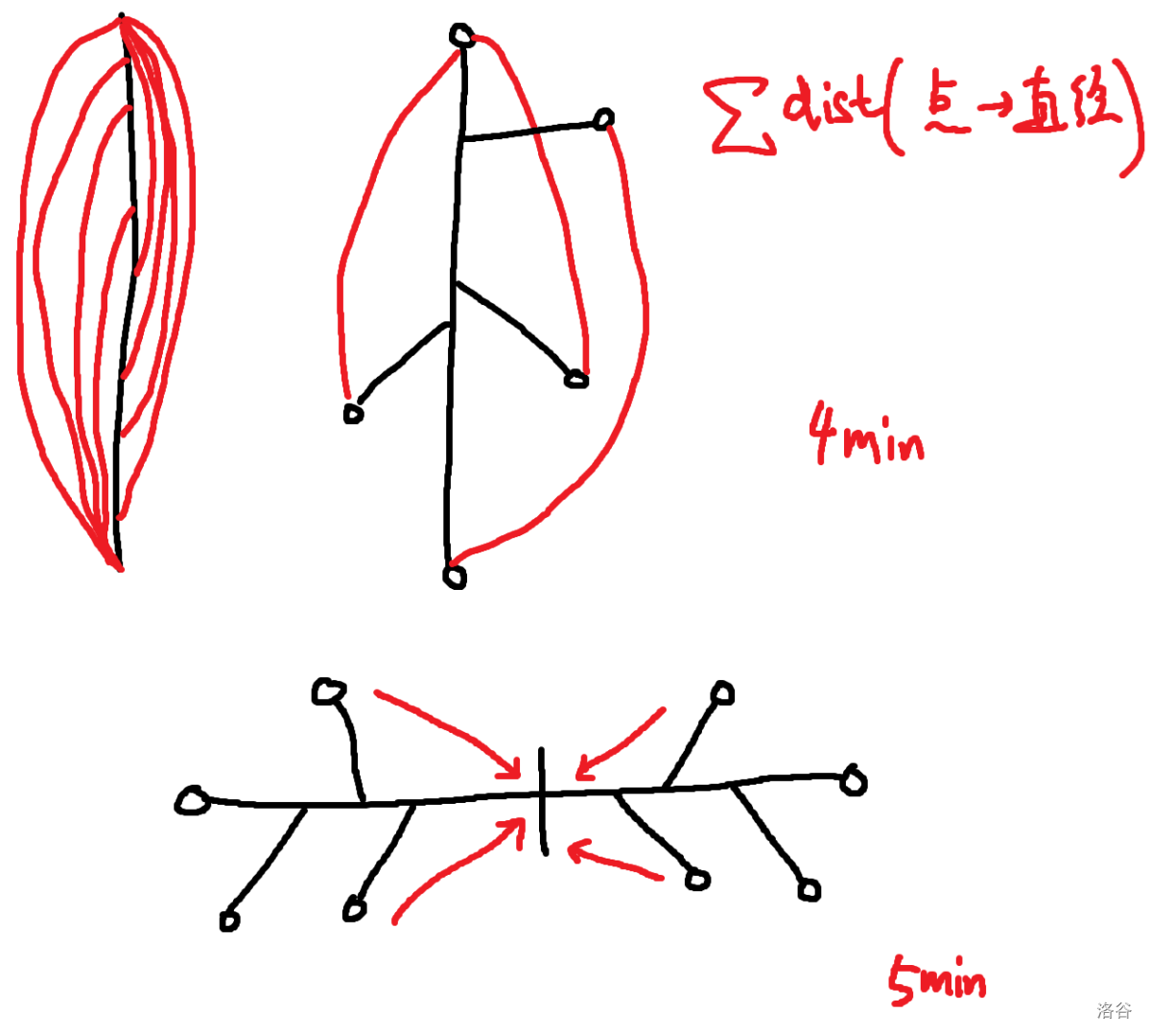
4min:我们画图推一下性质,先看链,发现是每个点到链的远端连边就行,然后考虑推广到树上,随便选一个直径,每个点到直径的远端点连边就行,这样的 $n$ 条边还需要去掉两个直径之间多连的边。
5min:可以二分出直径中点,然后 top tree 直接维护。
难度评测:下位紫。
### P11977 [KTSC 2021] 卡顿 / lag
6min:看着就是个回的弱化版,尝试用差分到极致来做。第一种情况是一维等差数列的矩形加,差分成 2-side 矩形修改,然后考虑修改对询问的贡献,是一个二维数点的形式。
11min:斜着的情况更复杂一些,转 $45$ 度之后变成 6min 类似的东西,还需要把边界处理一下。
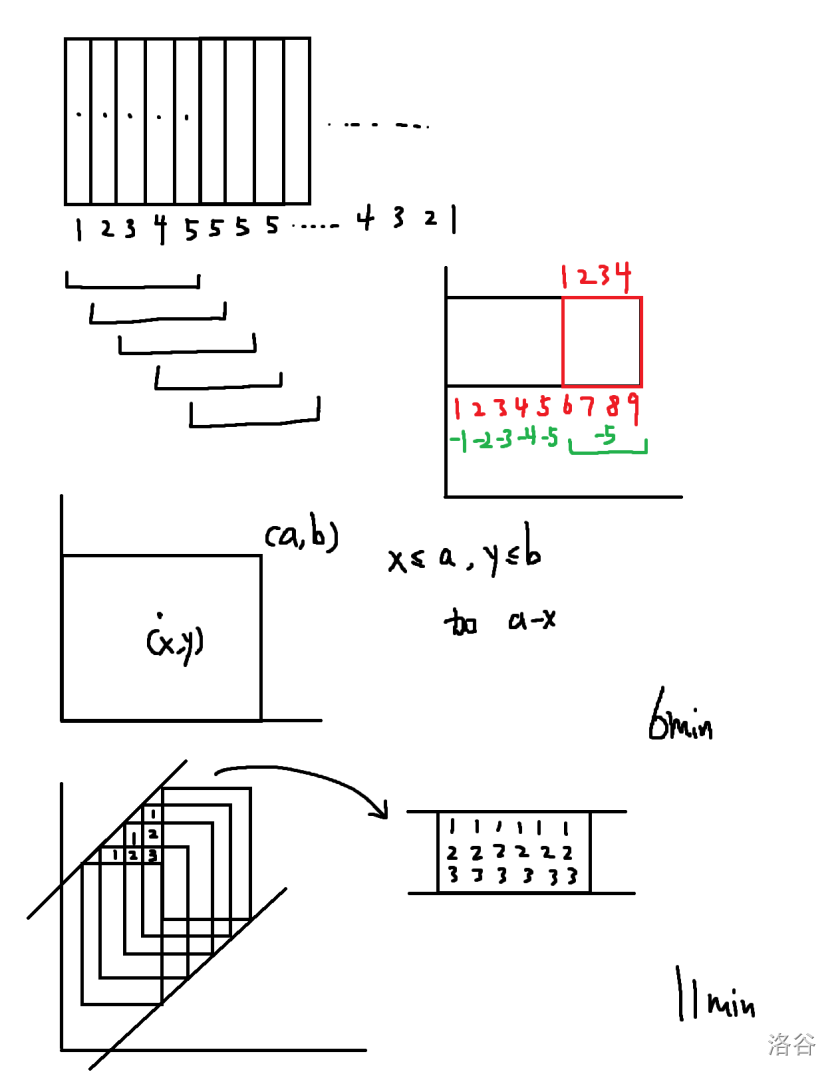
难度评测:中位紫。
### P11982 [KTSC 2021] 路灯 / streetlight
3min:类似动态笛卡尔树的样子,每次将一个位置改大会删掉若干个包含该位置的区间,改小则会加回来很多区间。
改小很麻烦,所以做线段树时间分治。现在问题变成插入和撤销,所以要不带均摊地维护路灯变化结构。
把路灯的线段画出来,可以发现要么不相交,要么包含,构成树结构。然后就做完了,维护一棵动态树,每次修改的时候二分出被删掉的路径,然后只会增加 $O(1)$ 个新的树上的点。
20min:补全细节。这个动态树不是标准形式,儿子是有序的,需要支持两种操作:
1. 将某个点的第 $x$ 到 $y$ 个儿子分裂出来,接在一个新的点上。
2. 将某条路径上的所有点的左边儿子按顺序分裂出来,接在一个新的点上。
第一部分可以直接用 WBLT 维护 rake tree,在其上面分裂出 $O(\log n)$ 个结点,对应该区间的儿子。
第二部分可以参考 WBTT,对每个 compress cluster,实际上维护成三部分,左边的儿子按顺序合并的结果,中间的路径按顺序合并的结果,右边的儿子按顺序合并的结果。每次 $2$ 操作沿着重链走的时候,顺便将沿途的所有左边儿子的 cluster 分裂出来。
这里会导致该路径变轻,可能产生轻重链切换,用 WBTT 的方法可以维护。
最后将分裂出来的 cluster 统一带权分治,合并为一个 rake cluster。
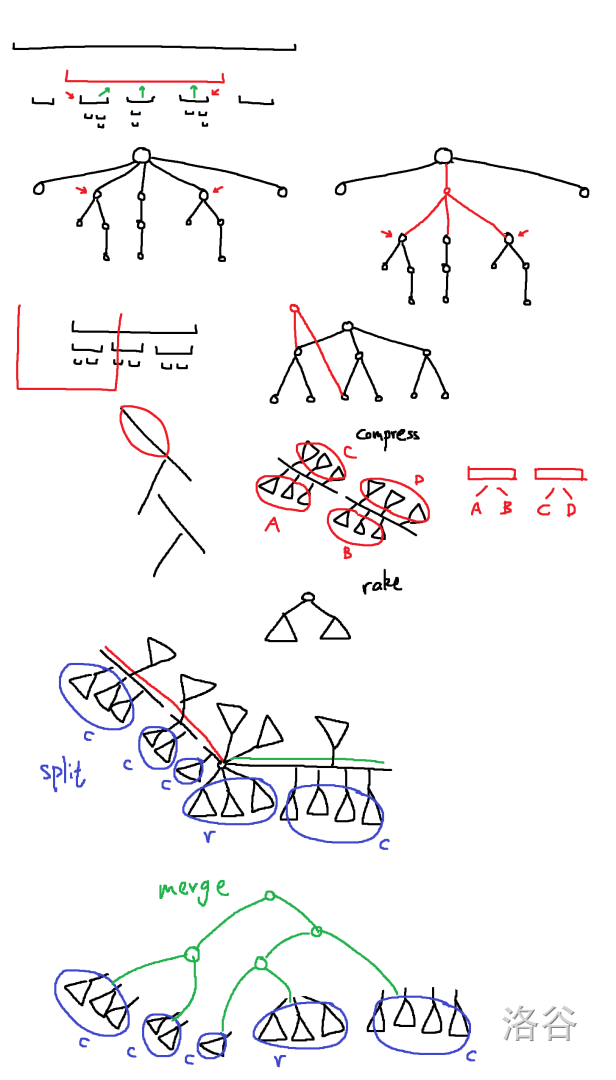
难度评测:下位黑。