题解:P10714 【MX-X1-T2】「KDOI-05」简单的有限网格问题
WZWZWZWY
·
·
题解
啊吧啊吧,被打回了。原因是“大数字应使用科学计数法表示”,于是我改成了 mod=10^9+7。(话说 1e9+7 不是科学计数法吗?)
从下往上看↑(真实事件未改编)
题意避坑
这道题坑也是非常的多。
一:
目标是在恰好两步内获得尽可能多的星星,然而小 S 不会玩,于是每次就会随意挑选一个可以移动到的新位置进行移动。
前一句话我给她划掉了,因为这是误导句。后面一句才是重点,千万不要用正常人玩游戏的思维!
小 S 随意移动。
二:
每次操作,你可以将捕捉器移动到同行或同列的某个位置,使得新位置与原位置不同且必须保证新位置 (x',y') 满足 1\leq x'\leq n,1\leq y'\leq m。捕捉器会捕捉 (x,y) 到 (x',y') 路径上所有的星星。一个星星被捕捉后将会消失。
- 也就是说,你每次可以上下左右移动任意格,就像象棋里的车。但是每次必须移动,移动两次。这路上经过的所有星星都会被吃掉。
比如可以这么移动:
(1,1)\to(1,2)\to(1,3)
这就算两步。是一个方向也可以。(因为小 S 不会玩啊,随意移动)
那么小 S 还可以有什么操作呢?
初始点 (1,2),有星星的点 (1,3)。
(1,2)\to(1,1)\to(1,3)
(1,2)\to(1,3)\to(1,1)
都可以。
还有,注意到新位置 (x',y') 满足 1\leq x'\leq n,1\leq y'\leq m。也就是说:
- 地图的最小坐标是 (1,1),而不是 (0,0)。
三:
(x,y)\neq(p,q)
+ 初始点上不会有星星。
#### 四:
> 每个位置上可以有多颗星星。
就在“输入格式”里,原话……
目前只记得这些,还有什么容易踩到的坑,欢迎在评论区交流!
------------
### 样例解释
很多人第一个样例都只找到了共 $10$ 颗星星的路径。
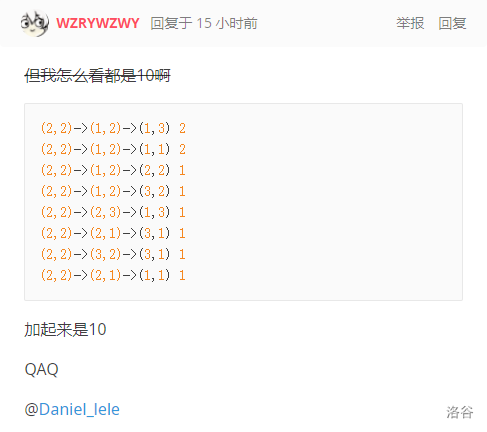
(左边是路径,右边是可以得到的星星数,忽略没有星星的路径。这里少了一条。)
剩下一条,看了上面“避坑”,你应该能找到。
$$(2,2)\to(3,2)\to(1,2)$$
得到 $1$ 颗星星。所有路径总共 $11$ 颗。
------------
### 思路
对于**每一颗星星**,计算初始点到它的路径数量 $cnt$。最后累加 $cnt$ 计入答案。
------------
### 推导式子
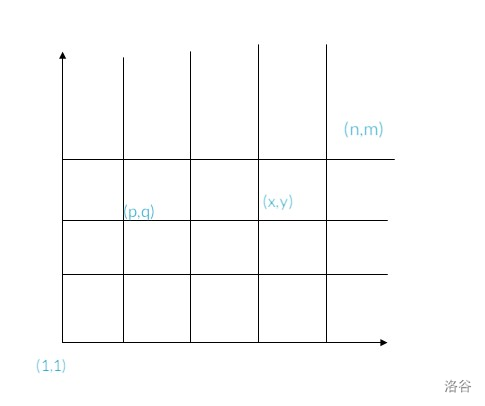
~~用电脑绘图累死我了,还不快点个赞!~~
当在同一行或同一列时,拿 $p<x,q=y$ 举例:
首先,第一步只能向左走,对吧?否则两步到不了 $(p,q)$。
若从 $(x,y)$ 第一步走到 $(p,q)$ ,可以上下左右移动任意步(但步数 $>0$,$1\le x'\le n$,$1\le y'\le m$),所以总共有 $(n-1+m-1)$ 种结果。
也可以第一步向左超过 $(p,q)$,这时第二步也是上下左右任意移动,$(n-1+m-1)$ 种结果。
若第一步没有走到 $(p,q)$,或者先向右走,那么第二步必须走到 $(p,q)$,或者超过 $(p,q)$,才能吃到它,总共有 $(n-p-1)\times (p-1)$ 种结果。
那么加起来就有 $(n+m-2 + n-p-1) \times p$ 种结果。
其它三个方向(上、右、下)同理。
------------
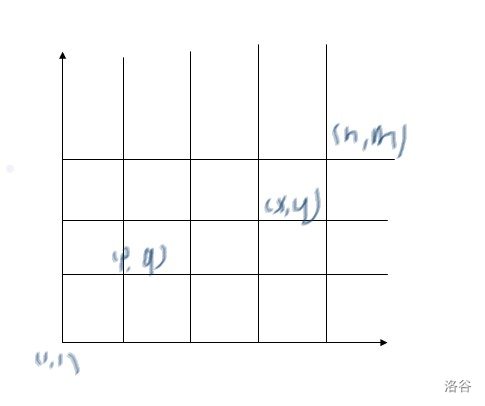
不在同一行或同一列。
拿这个图举例。
显然,有两种路径到达 $(p,q)$,分别是 $(x,y)\to(p,y)\to(p,q)$ 和 $(x,y)\to(x,q)\to(p,q)$。
这个时候已经用了“两步”了,不可能再转向。但是——这个时候最后一步可能没有走完,可以继续往前走。
可以 $(x,y)\to(p,y)\to(p,1)$。
那么显然地,最后一步向下的方案数为 $q$,向左的方案数为 $p$。
总的方案数是 $p+q$。
其他方向同理。
------------
### 代码
**忠告**:$mod=10^9+7$ 不要取错。每次乘法都要取模。$1\leq n,m\leq10^{18}$,不开 `long long` 见祖宗。
(考场代码,保险起见都加上了取模。可能稍微合并了一些公式。)
```cpp
cin >> p >> q; // 每个星星的横、纵坐标
int cnt = 0;
if (p < x) { // 横坐标比初始点横坐标小
if (q < y) cnt = p % mod + q % mod; // 纵坐标比初始点小
if (q > y) cnt = (m-q+1) % mod + p % mod; // 纵坐标比初始点大
if (q == y) cnt = (n+m-2 + n-p-1) % mod * (p % mod) % mod; // 纵坐标相等
} else if (p > x) {
if (q < y) cnt = q % mod + (n-p+1) % mod;
if (q > y) cnt = (m-q+1) % mod + (n-p+1) % mod;
if (q == y) cnt = (n-p+1) % mod * ((n+m-2 + p-2) % mod);
} else { // 横坐标相等
if (q > y) cnt = (m-q+1) % mod * (((n+m-2) % mod + q-2) % mod);
else cnt = q % mod * ((m+n-2 + m-q-1) % mod);
}
ans += cnt;
```
还有什么不懂的或者想吐槽的可以在评论区讨论。