Segment tree beats 的时间复杂度下限为 2log
Tony2
·
·
算法·理论
原问题为 https://jiry-2.blog.uoj.ac/blog/1404 即区间加区间 chkmax 区间和的复杂度问题。
此 Hack 经过 negiizhao 的优化已应用到 https://uoj.ac/problem/169 并成功 Hack 了大量代码。
Part 1: Hack 方式介绍
Hack 序列如何转化到线段树上
首先给出一个长度为 len 的 Hack 序列,使得这个序列在进行 O(1) 次的区间加操作和 \Theta(\log len) 次的全局 \text{chkmax} 操作后变为原序列的一个轮换。因为轮换并不会影响我们进行区间加和全局 \text{chkmax} 操作(给区间加的下标同时轮换一下即可),所以可以视作序列没有改变。
如果我们有了这样的序列,令 len=n^{\frac{1}{3}},并每隔 n^{\frac{2}{3}} 放一个这样的序列,每个序列刚好对应一个线段树区间。长度为 n^{\frac{2}{3}} 子树内恰好都包含了这样一个线段树区间。
对 Hack 序列,进行的区间加操作是一个一个区间操作的,但是 \text{chkmax} 操作只需要全局一个指令就能一起执行。也就是一次 \text{chkmax} 操作可以递归到这 n^{\frac{1}{3}} 个 Hack 区间,每次至少调用了 \Omega(n^{\frac{1}{3}}\log n) 个线段树节点。而 \text{chkmax} 操作统一执行 \log len=\log n 次,故总访问节点数为 \Omega(n^{\frac{1}{3}}\log^2 n)。
区间加操作和全局 \text{chkmax} 总共进行了 O(n^{\frac{1}{3}}+\log n)=O(n^{\frac{1}{3}}) 次,把访问节点数除以查询(操作)次数,得到平均单次访问节点量为 \dfrac{\Omega(n^{\frac{1}{3}}\log^2 n)}{O(n^{\frac{1}{3}})}=\Omega(\log^2 n)。
Hack 序列的构造
代码可见 Tony2 的 generator 或 negiizhao 的改版。
我的 gen 里面 vf[n] 存的就是一个长度为 \text{Fib}_{2n+1} 的 Hack 序列。其中 \text{Fib}_0=0,\text{Fib}_1=1。
将代码转化后:
-
对一个 n 阶 Hack 序列,先将前 \text{Fib}_{2n} 个数减去 \text{Fib}_{2n-1}。
-
把后 \text{Fib}_{2n-1} 个数加上 \text{Fib}_{2n}。
-
全局对 \text{Fib}_{2n} 做 \text{chkmax} 操作(这里会影响到 n 个不同数字,也就是说实际上可以拆解成 n 次 \text{chkmax} 操作,其中 n-1 次将最小值和次小值合并,触发原算法的访问条件)。
-
把第 \text{Fib}_{2n} 个数改成 0。
发现此时序列恰好为原序列向右轮换 \text{Fib}_{2n} 次的结果。
我们知道 \log\text{Fib}_{2n+1}=O(n),所以这个过程中有效的 \text{chkmax} 操作确实达到了 \Theta(\log len) 次(len=\text{Fib}_{2n+1})。而区间加和单点修改操作只有 O(1) 次。满足 Hack 序列的要求。
构造方式可参见代码。至于构造为什么能得到如上性质,我并不是一开始就找到序列的,是通过一个结构推得序列的。
不想看后面的可以直接看一个 n=3 的例子。
19 16 17 16 8 14 11 12 11 8 9 8 0
将后 5 个数加上 8,前 8 个减去 5。
14 11 12 11 3 9 6 7 19 16 17 16 8
全局对 8 进行 \text{chkmax}。这一步实际上是对 3,6,7,8 依次进行的。中间两步都会减少不同数字个数。
14 11 12 11 8 9 8 8 19 16 17 16 8
把第 8 个数改成 0。
14 11 12 11 8 9 8 0 19 16 17 16 8
为了方便起见,向右轮换 5 次。
19 16 17 16 8 14 11 12 11 8 9 8 0
序列无改变,Hack 成立。
Part 2: 结构是什么/怎么找到的
定义两种结构 f_n,g_n。定义两个数列 a_n,b_n。
定义 a,b:
a_0=b_0=0
a_1=b_1=1
b_n=a_{n-1}+b_{n-1},a_n=a_{n-1}+b_n
我们发现其实 a_n=\text{Fib}_{2n},b_N=\text{Fib}_{2n-1}。
定义 f,g:
f_0=g_0=\{(0,1,0)\}
f_n=\{(0,a_n+b_n,0)\}\ \cup\ add(f_{n-1},(0,a_n+b_n))\ \cup\ add(g_{n-1},(b_n,a_n))
g_n=f_n\ \cup\ add(g_{n-1},(a_n+b_n,0))
其中三元组 (x_1,x_2,y) 代表了一个线段 (x_1,y)\sim (x_2,y)。操作 add(S,(\Delta x,\Delta y))=\{(x_1+\Delta x,x_2+\Delta x,y+\Delta y)|(x_1,x_2,y)\in S\}。
首先我们要把线段理解成一个树上的 f 型节点。每个 f_n 都会创造出一个 n_f 节点,并且其左儿子为一个 n-1_f 节点,右儿子为一个 n-1_g 节点。而对于 g_n 来说它会创造出一个左儿子为 n_f 节点、右儿子为 n-1_g 的 n_g 节点。
注意这里 n_f,n_g 的指代只是一种分类,代表一个节点的类型。一个树里面可以有很多个 n_f 节点。
这样交替迭代的过程生成出一棵树。假设树根为 n_f,我们先观察一下这个树的一些性质。
树根 n_f 对应的节点为 (0,\text{Fib}_{2n+1},0)。
$a_n=a_{n-1}+b_n$。这个式子之后会有作用。
对树上的任意一个节点显然都有一个对应的 $x$ 区间 $[l,r]$。
接下来进入最关键的部分,把树裂解成两份并重新组装。选取 $x=a_n+0.5=\text{Fib}_{2n}+0.5$ 处将树裂开,即删除所有满足 $l\le x< r$ 的节点。这样被删掉的节点有可能是 $f$ 节点也有可能是 $g$ 节点。
奇迹出现了:被删除后,树的左侧在平面上形成了一个新的 $n-1_g$ 节点的形状。树的右侧形成了一个不完整的 $f_{n-1}$ 节点,缺少了一些线段,我们试图将其补齐:第一条要补的线段在 $y=a_n-a_{n-1}=b_n,x_1=a_n,x_2=a_n+b_n$ 处。之后的线段都满足 $x_1=a_n$,恰恰是被切开的位置。下一条线段的位置很好找:在 $y=a_n+b_{n-1}=a_n+a_{n-1}-a_{n-2}$ 处。
树的左侧部分是好理解的,由于留下了 $n-1_f,n-2_f,...$,这些节点自然形成了一个 $n-1_g$ 节点。实际上这是因为 $n_g$ 是 $n_f+n-1_f+...+0_f$,这可以简单地从递推式中得到。所以这些 $n-1_f,n-2_f,...$ 就会被后缀和得到 $n-1_g,n-2_g,...$。
树的右侧部分手动添加的线段为什么合法?实际上,当 $n_f$ 被删除时,留下来的是 $n_f$ 的右儿子 $n-1_g$ 的右儿子:$n-2_g$。下一个留下来的节点是 $n-3_g$。他们的 $y$ 的差是 $a_n+a_{n-1}-a_n=a_{n-1}=b_{n-1}+a_{n-2}$。为什么要拆成 $b_{n-1}+a_{n-2}$?这表明如果此时在这两个节点中间插入一个 $n-2_f$ 节点,那么它的右儿子恰好是 $n-3_g$,并且 $y$ 差了 $a_{n-2}$;父亲应当是 $n-1_f$,父亲的右儿子和左儿子的根节点的 $y$ 的差恰好是 $b_{n-1}$。这完美满足了初始构造的结构。最终我们只需要将树的两侧调整平衡(左侧减 $b_n$,因为根应该要在 $y=a_n$;右侧加 $a_n$,因为根应该要在 $y=a_n+b_n$)并左右交换,再把原本的 $(0,a_n+b_n,0)$ 补回去就得到一开始的树了。
接下来我会把 $n=3$ 的情况在 GeoGebra 绘制出来。
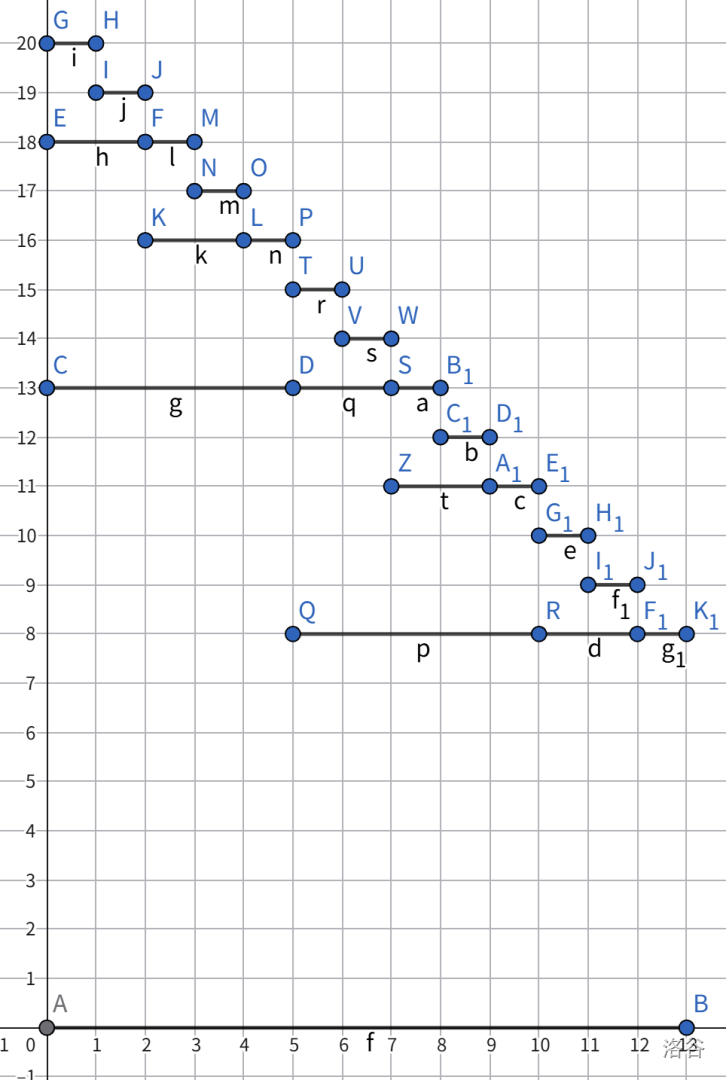
这是 $3_f$ 的结构。每一条线段都代表了一个 $f$ 型节点的根。而 $g$ 型节点是隐藏的,例如 $(5,13,8),(10,13,8),(12,13,8)$ 就分别是一个 $2_g,1_g,0_g$ 节点的根。
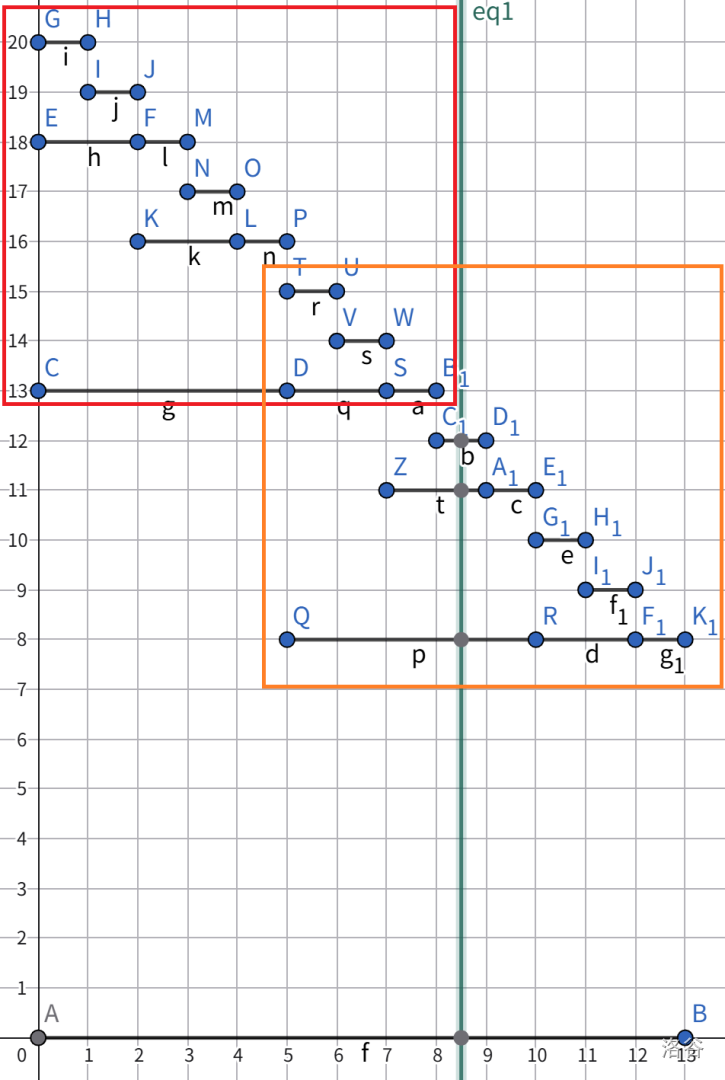
当树被切开时,我们发现左侧完全就是一个 $2_g$ 结构,尽管 $(0,8,13)$ 之前并不是一个节点,但我们可以将其设置为节点了。
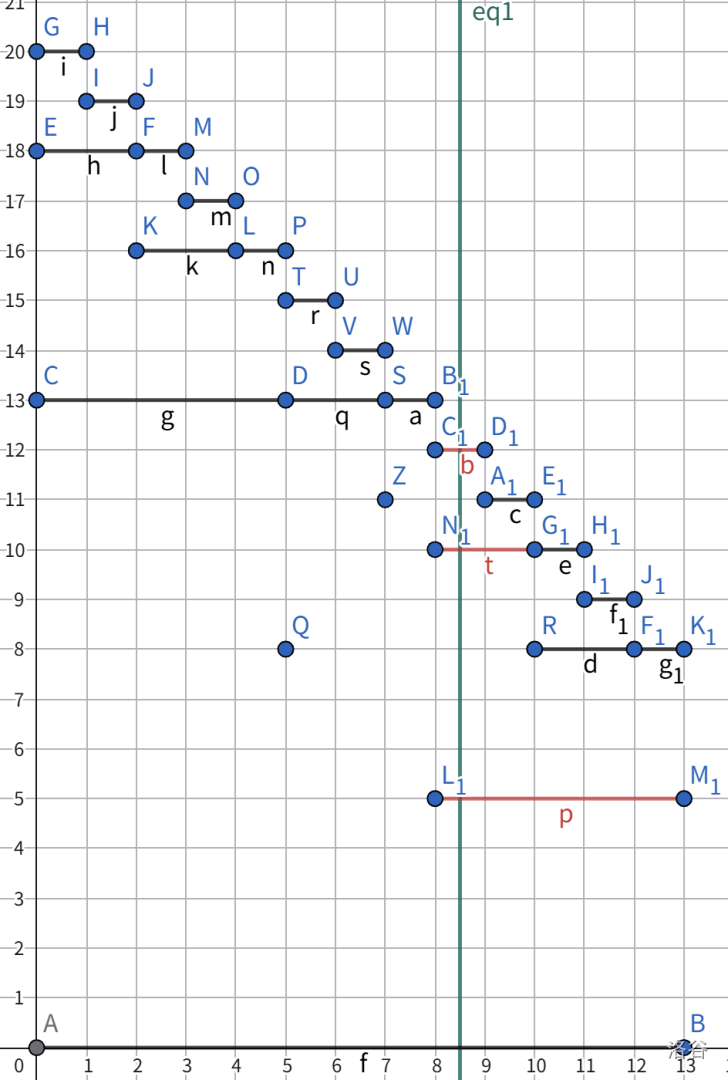
把原本被绿线切开的线段删除之后,我们补回三条红色线段。这样 $x=8$ 及其右侧就形成了一个以 $(8,13,5)$ 为根的 $2_f$ 结构。
之后把左右两边调换上下平移一下就回到原本的结构了。
此时我们将 Hack 序列嵌入其中。对于任意一个 $n_g$ 节点,我们会在其左端点处得到一个点 $(x,y)$,这个点的意思是序列的第 $x$ 项是 $y$。我们把这个想法标在 $n=3$ 的情况上。
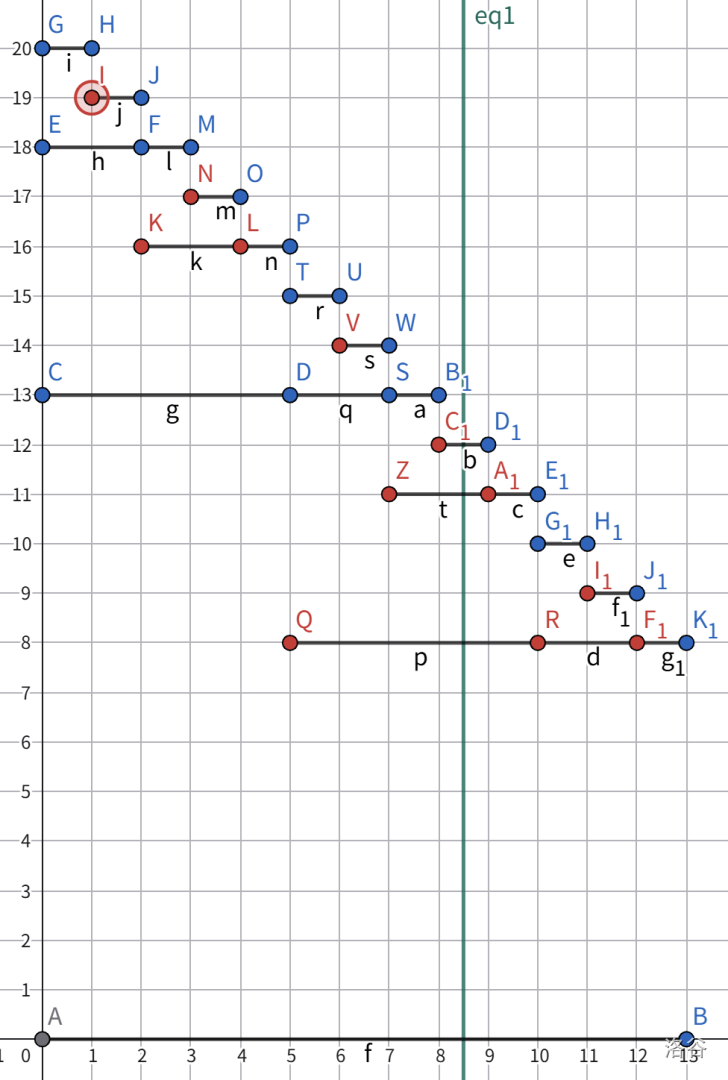
红色的点代表着序列上的点。沿着绿线切开时,有趣的事情发生了:$(5,13),(7,13),(8,13)$ 应该成为新的红色点,因为这里出现了一个 $2_g$。但是原本的红色点在 $(5,8),(7,11),(8,12)$,我们需要对这三个位置对 $13$ 进行 $\text{chkmax}$ 操作才能得到正确的结果。这恰好就是我们想要 Hack 的东西:操作变为对 $[1,8]$ 对 $13$ 进行 $\text{chkmax}$ 操作。简单调整一下就变成全局 $\text{chkmax}$ 操作了。把结构左右交换实际上是没有进行的,所以整个序列被向右轮换了 $a_n$ 轮。而图中的 $(5,8)$ 在轮换后并没有出现,但只需要令 $(13,0)$ 也是红色点就能满足条件了。
那么这个结构是怎么找到的呢?这就要从很久远的理论推导说起了。首先我们的模型是对一个序列进行区间加操作和全局 $\text{chkmax}$ 操作。因为我们需要对所有序列进行分析,我们只能保留这些操作后序列的性质。例如进行 $\text{chkmax}$ 操作后,我们一定知道被 $\text{chkmax}$ 的值操作后都是一样的,并且剩余值一定比它们大。所以我们可以用这些大小关系建立出笛卡尔树(森林)。为什么是森林呢,因为区间加操作(实际上是后缀加)会让一些大小关系断开。也就是让笛卡尔树分裂。
在这里我经过了长时间的推导并没有得到证明。于是我转向使用“崩解对”的理论来预测“不同数字个数”这个值的变化。(这里其实是因为 $\text{chkmax}$ 操作每次只会减少一个“不同数字个数”,如果能让这个值增长很快却能多次使用 $\text{chkmax}$ 操作减少,那么就能成功 Hack 了。)崩解对的定义就是:假设有一对位置 $(p_1,p_2)$,它们会在某次 $\text{chkmax}$ 操作后值一直相同,直到某次区间加操作破坏了这个性质。一个崩解对会在 $(p_1,p_2)$ 所属的笛卡尔树为同一个直到被那一次区间加操作断开的这一次**使得笛卡尔树为同一个**的时刻出现。显然这个时刻应当是一个 $\text{chkmax}$ 操作,但其实这是无意义的,因为只要进行一次 $\text{chkmax}$ 操作,所有树都会被合起来。所以不妨说这是由一次区间加操作导致的断裂后重新补起来所产生的。
那么一个崩解对的生命周期是这样的:在一次区间加操作导致笛卡尔树断裂后产生,经过 $\text{chkmax}$ 操作确认其两个位置上的值相等,最后由一次区间加操作杀死这个崩解对。一共要进行三步,我们会用第一步、第二步、第三步来称呼这三个步骤。一个崩解对在第一步到第二步处于 $1$ 状态,之后处于 $2$ 状态。
观察发现崩解对之间形成了树的关系。第一步实际上进行的就是添加一条 $1$ 状态链。第二步会让一些崩解对变成 $2$ 状态并且这些崩解对之间的值其实是相同的,也就是说会产生一个隐形的枷锁,这个枷锁的作用是防止在第一步的时候,即添加 $1$ 状态链的时候,把原本具有相等关系的崩解对切开,也就是说这些被枷锁控制的崩解对需要在被区间加操作断开之前处于同一个节点的儿子内(当然从中间断开后枷锁会分裂成两个)。第三步就是把一条从根开始的 $2$ 状态链删除。
由于在上述观察中枷锁的概念过于抽象,我转而将问题转化为限制每次 $\text{chkmax}$ 操作一定会使得一些 $(p_1,p_2),(p_2,p_3),...,(p_{k-1},p_k)$ 处于 $1$ 状态的崩解对变成 $2$ 状态并被控制在一个枷锁下。这实际上就是在这些崩解对的头顶上加了一个新的节点来防止被分开。
最终突破瓶颈的是一个观察:每次第一步添加的 $1$ 状态链一定是自顶向下被染色成 $2$ 状态的,而且必须是染色、删除、染色、删除这个顺序。这让我们把这条 $1$ 状态链直接写成一个节点,只是这个节点有很多个儿子,每次删掉一个而已。$2$ 状态的保障其实正来源于上述的“枷锁”节点。到现在一个模型出现了:树有一些枷锁节点和原本的节点。不妨称之为方点和圆点。我们不妨直接令圆点下一定是方点,方点下一定是圆点。第一步就是造一个圆点出来,可以让几个方点根变成它的儿子。第二步就是造一个方点出来,可以让几个圆点根变成它的儿子。第三步就是删除一条方-圆链,但是实际上只删除其中**边**。这明显让我们联想到了**并查集**单路径压缩模型:删除链中间的边并合并到一个点下方恰恰就是路径压缩干的事情。只不过这里的模型有圆点和方点。
拿到这个模型后我就有很大把握 Segment Beats 可以被 Hack 了。接下来我做的事情就是去学习了二项堆 Hack 并查集单路径压缩的方法并套用到了这个上面。上面分析中的 $f$ 的根实际上都是崩解对。$f$ 一直往左走的这一堆 $f$ 说的就是一个圆点下的多个儿子的模型。处于 $g$ 中的 $f$ 节点(除了最后一个,那个更像是一个辅助的节点)就是被枷锁,也就是 $g$ 保证已经两边相同的 $f$ 节点就是处于 $2$ 状态的崩解对。其余是处于 $1$ 状态的。上面搞的分裂操作恰恰就是为了杀死一些崩解对并产生新的。所以说崩解对就是圆方树中的边、$f,g$ 体系中的线段。这些东西是基本等价的。
最后在参考了并查集单路径压缩 Hack 后,我设计出了这个递归构造的模型。遇到的唯一问题就是 $a,b$ 应该填什么。幸好在分析了两边的性质之后这个数列是能被解出来的。最后都是斐波那契数列。
## Part 3: 杂谈
Segment tree beats 这个算法是 jry 老师在 2016 年提出的。但是我有点找不到我当时学这玩意看到的 ppt 了,总之就是一个背景是 AngelBeats! 的 ppt。当时很菜,根本没去理解时间复杂度。
直到 11.13 我看到了 u 群有人在讨论这个问题,随即开始思考。我的第一步思考是关于一个序列的“颜色数”变化的性质。我试图刻画一个序列的未来的颜色数曲线的改变量,问题转化到了排列上,但立刻陷入了困难中。
差不多之后的第二天还是第三天,我思考了关于序列建立笛卡尔树森林的想法。但是当时这个笛卡尔树没有考虑 `1 2` 这种大小关系,所以根的数量会随着区间加操作,即对树的切割,发生突变。至此又卡住了一段时间。
大概又过了一两天,我想到了完整的笛卡尔树。此时树根数量的变化变得合理了,但是 chkmax 操作仍然会让树的形态发生奇奇怪怪的变化。我试图建立类似圆方树的结构直接分析各种点数的变化,却发现这样一定是徒劳的,很多信息是线性相关的。
然后我发现可以通过“崩解对”来预测未来的相同颜色对的崩解。在两个树合起来的时候,会产生一些崩解对,裂开的时候会去掉一些。chkmax 操作能够让一些崩解对真正成为相同数字对。这里的三个操作成为了之后研究的基石。当时我在仅保留两个操作的情况下给出了伪证。
该伪证发布之后有一些人试图去理解它。在 critno 老师的帮助下,我找到了这个证明的漏洞,证明崩塌了。在长时间的打补丁失败之后,我试图进行 hack。我发现了一种 hack 思路,其思路形如并查集,但是我却发现中间漏掉了 chkmax 操作会将崩解对“合并”的性质,hack 爆炸了。
至此陷入了长时间的挣扎时间。在“合并”性质的帮助下,整个结构显得无懈可击;同时操作又有高达三个,去掉任何一个或者任何一个性质都会直接得到错误的 hack。中间思考过“怎样的 1 3 步骤是对 2 步骤合法”的问题以及“是否存在一个模型使得 加入一条链后 包括确认,删除的次数减少?”的问题,都没法得到合理解释。
最终撬开裂缝的是一个性质:单次添加的崩解对形成的链一定是从上到下染色并被删除的。模型更正为一个类似于圆方树的并查集模型,立刻能看到 hack 的希望了。也就是这几天左右,我学习了并查集 hack 单路径压缩的方法,并套用到了这个上面;在因为写普物作业而昏头想错一天之后,终于在 12.23 找到了非常接近 hack 的结构。
这一天我非常激动,因为我感觉离终点已经非常近了。创造结构,填写各项数值,解出数值的递推式,最终获得了在 0.618 处进行区间加操作的优美结构。这一次终于不会再假了,1log 的证明已经不会再存在了。
之后应该已经有一些人理解了这个 hack,但要理解这个 hack 怎么来的应该有点困难。我是在草稿纸上画了很多张图才和室友 zxb 解释清楚 hack 的原理的。草稿纸上的内容已经写在上面的图片了。
最后感谢所有愿意在一开始听我疯狂伪证的朋友和曾经试图证明/Hack 过这个东西的人。最后能够是我拿到这一份 Hack 是我的荣幸。