题解 P5209 汉诺塔
wuzr
·
·
题解
这里用 m 表示相同大小的盘子数。
如果不对最终状态进行限制,那么最优解显然和普通的汉诺塔一样,每一层都分三步:把上面一些小的移到中间,把大小相同的 m 个移到最后,把中间小的移动到最后。可以发现,每一步移动的所有盘子的相对顺序都会反过来。我们把这样的移到称为初始的。
现在对终止状态进行限制,这就意味着每一层在某几次移动的时候与上述表现出来的行为不同。我们可以把每一次移动看成对当前盘子的相对顺序进行置换。即对于第 i 层,假设它被移动了 K 次,那么我们要做的是找到一些置换 p_1,p_2,...,p_K,使得他们乘起来等于我们需要的排列。
在汉诺塔中这个 K 可能很大,但是不难发现其实大部分移动都是初始的(无限制时的最优),每次至多只有 m! 种变化(超过 m! 一定会出现重复状态)。
我们的思路就是大部分情况下使用初始的移动,同时 \text{DP} 发生变化的部分。
现在考虑底层的移动对高层的影响,在假设高层都是初始的移动的情况下,可以发现每一层对高的层的影响只停留在高的层移动的奇偶性(奇数的时候在初始移动下是倒置的)。
这里举个例子:
输入
1
2 2
1 2
2 1
输出
10
本组数据在无限制的条件下最终状态是:
2 1
1 2
我们改变了第 1 层的移动方式,影响到了第 2 层。
再举个例子:
即:
输入
```
1
3 2
1 2
2 1
1 2
```
输出
```
22
```
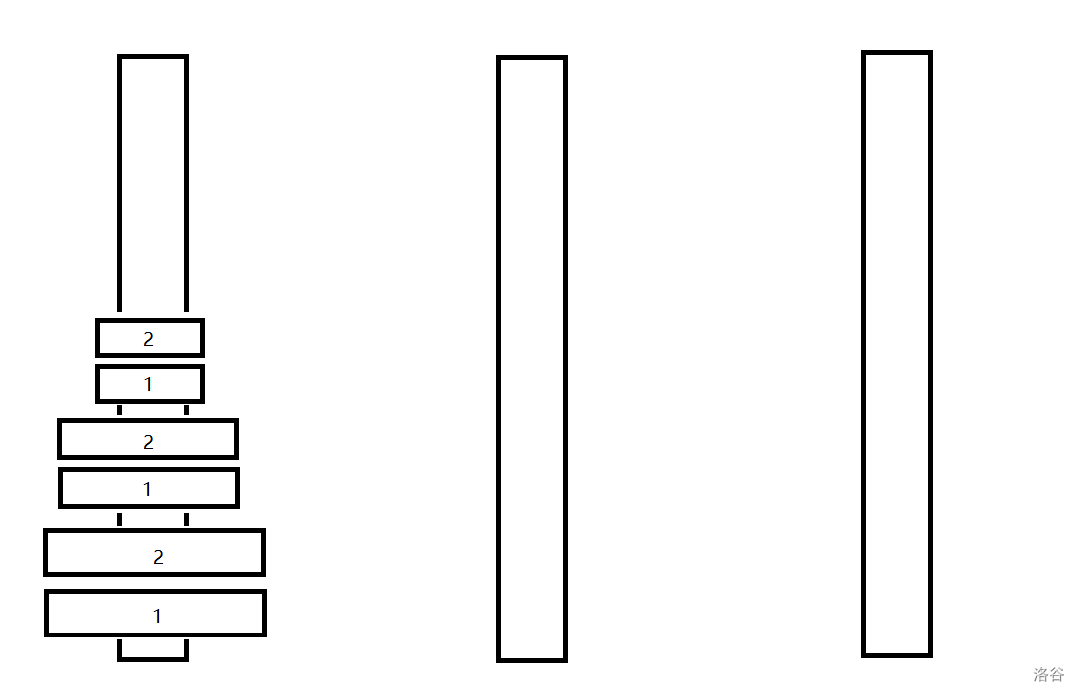
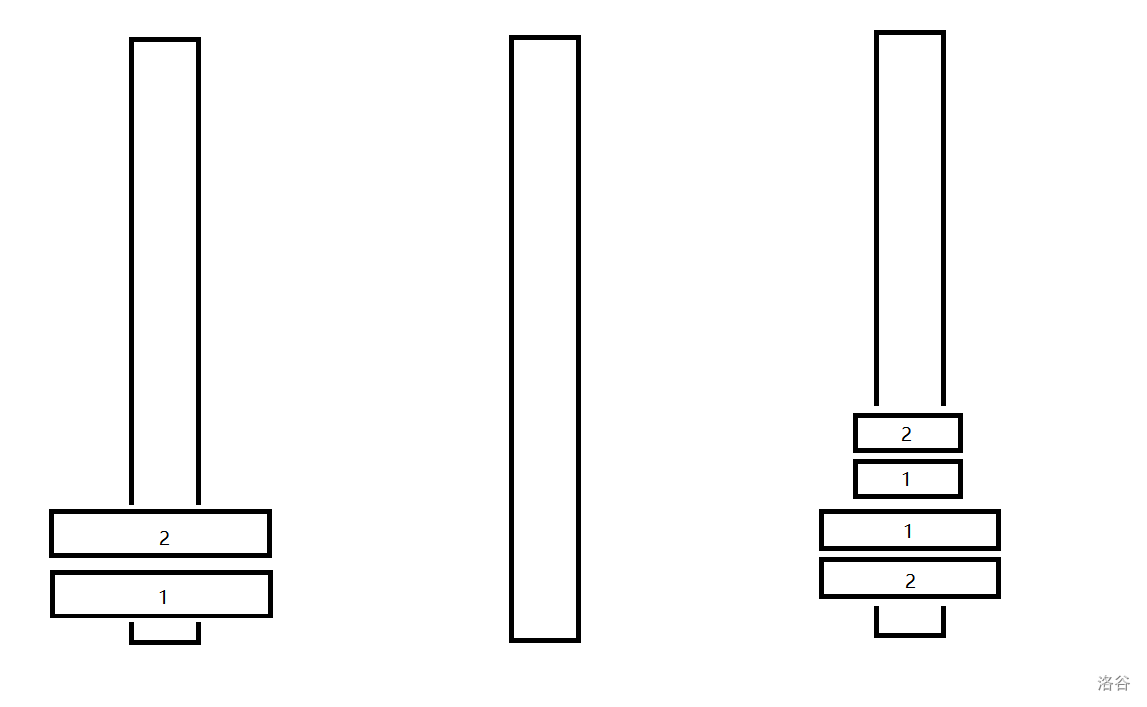
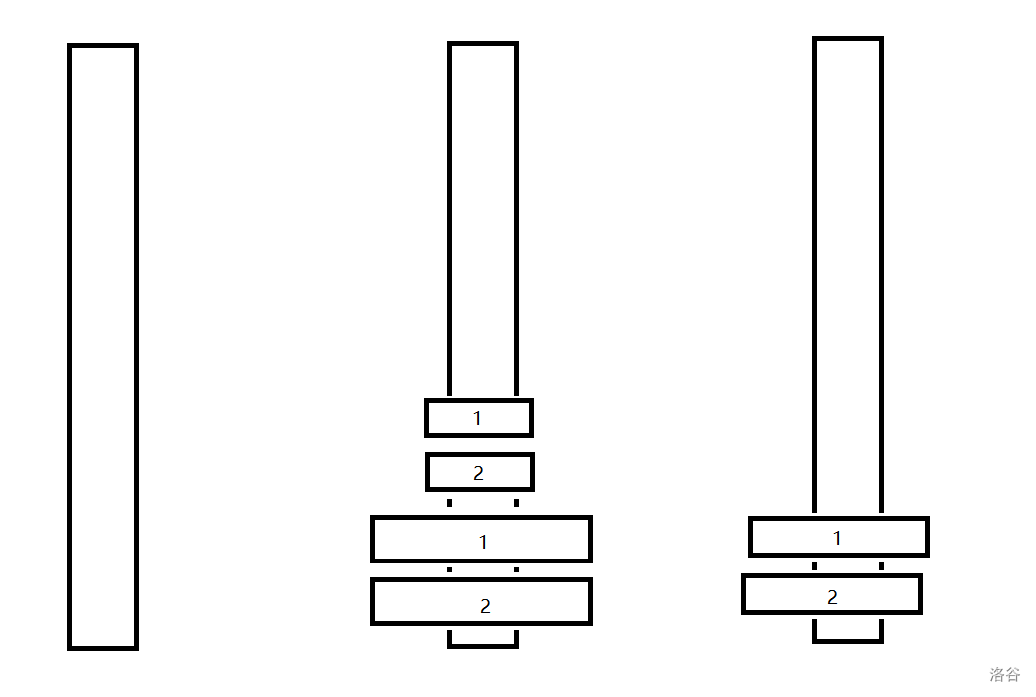

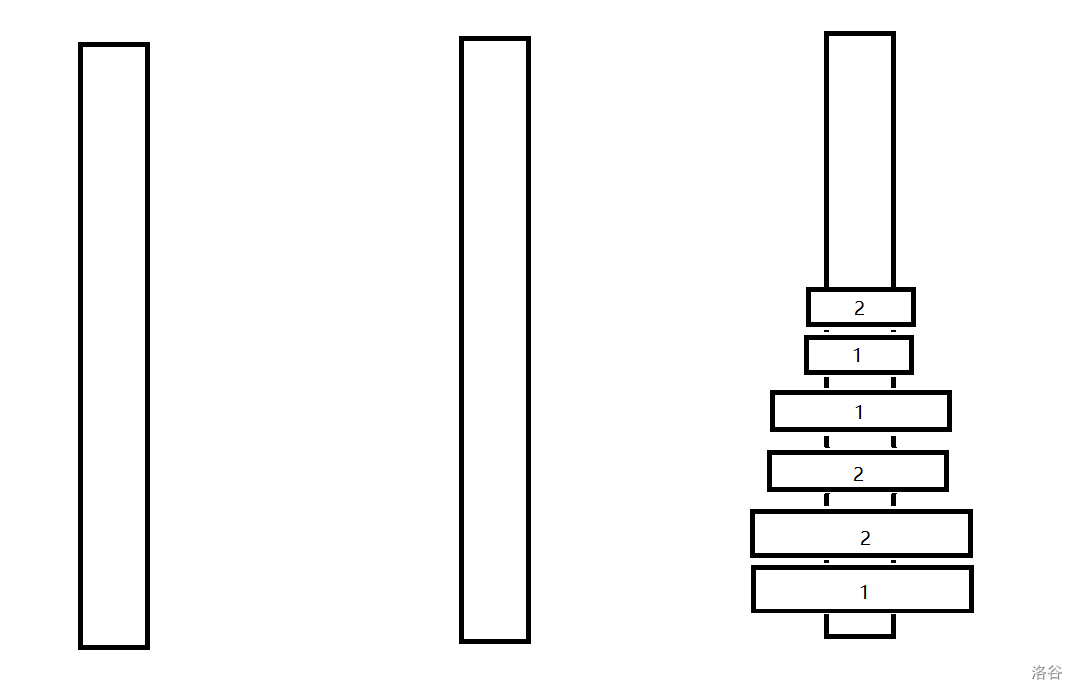
我们发现改变了第 $1$ 层只对第 $2$ 层有影响。
与无限制的条件下最优移动方案比,第 $2$ 层多移动了 $1$ 次,第 $3$ 层多移动了 $2$ 次(第 $3$ 层可以抽象为若干更高层,代码实现时将更高的抽象为一个点)。
于是更近一步的说,第 $i$ 层只对第 $i+1$ 层有影响(更高层在初始移动的情况下影响的步数都是偶数)。
同时因为我们的 $\text{DP}$ 是对初始的移动进行修改,因此我们还需要记录第 $i+1$ 层总共移动了多少步,步数不需要确切记下来,只要对 $m!$ 取 $\min$ 就可以了。
因此我们的 $DP$ 状态就是 $f[i][t][b]$ 表示当前 $\text{DP}$ 到第 $i$ 层,第 $i$ 层移动了 $t$ 步,以及移动次数的奇偶性是 $b$。在转移的时候我们需要处理这样的值 $w[i][t][p][t']$ 表示在第 $i$ 层用 $t$ 步移动出排列 $p$ 同时上一层移动次数增加了 $t'$ 的最小步数。
接下来我们考虑怎么处理这个值。
首先我们需要计算 $g[i][p][t']$ 表示在第 $i$ 层仅修改一次初始的移动得到置换 $p$,同时上一层的移动次数增加了 $t'$ 的最小步数。这一步中我们只需要考虑当前层的盘子以及上面的那一堆在哪里就可以了,状态数 $S$ 只有不到 $2000$ 种,把转移图建出来之后枚举 $i$ 跑最短路就可以了,时间复杂度约为 $O(m!nS)$。
接着从 $g$ 得到 $w$ 就是背包,时间复杂度约为 $O(n(m!)^4)$。
最后由 $w$ $\text{DP}$ 出 $f$,根据定义就可以了,稍加优化时间复杂度可以降到 $O(m!Tn)$。
参考ZJOI2017 Day2题解:https://wenku.baidu.com/view/4f242987d0f34693daef5ef7ba0d4a7302766ca6.html?_wkts_=1674962588966
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
ll rd() {
ll x = 0, f = 1;
char ch = getchar();
while (ch > '9' || ch < '0') {
if (ch == '-') f = -1;
ch = getchar();
}
do x = x * 10 + ch - 48, ch = getchar();
while (ch >= '0' && ch <= '9');
return x * f;
}
void wr(ll x) {
if (x > 9) wr(x / 10);
putchar(x % 10 + 48);
}
const int K = 7, N = 25, p[6] = {0, 1, 2, 3, 4, 0};
int t, n, k, fac[5] = {0, 1, 2, 6, 24};
map<vector<vector<int>>, int> mp[N];
int tr[N][N], mul[N][N], f[N][N][N];
ll g[55][N];
struct P {
int a[K];
void in() {
rep(i, 1, k) a[i] = rd();
}
int getid() {
int res = 0;
rep(i, 1, k) {
int sum = 0;
rep(j, i, k) sum += a[i] > a[j];
res += sum * fac[k - i];
}
return res + 1;
}
bool operator < (const P&x) const {
int i = 1;
for (; i <= k && a[i] == x.a[i]; i++);
return i <= k && a[i] < x.a[i];
}
int&operator[](const int&i) {
return a[i];
}
P operator * (const P&x) {
P ans;
rep(i, 1, k) ans[i] = a[x.a[i]];
return ans;
}
} pre[N], a[55];
struct sta {
vector<int> a[3];
int x, y;
// 最短路
bool work() {
per(i, x, 0) {
auto it = mp[i].find(vector<vector<int>>(a, a + 3));
if (it != mp[i].end() && it->second <= y) return 0;
}
mp[x][vector<vector<int>>(a, a + 3)] = y;
return 1;
}
};
queue<sta> q;
ll F(int x) {
return x < 1 << 24 ? x : 1ll << 60;
}
void solve() {
memset(g[n + 1], 0, sizeof g[n + 1]);
per(i, n, 1) {
memset(g[i], 50, sizeof g[i]);
int id = a[i].getid();
rep(j, 0, N - 1)
rep(p, 0, N - 1)
for (int l = 0; p + l < N; l += 2)
g[i][j] = min(g[i][j], g[i + 1][p] + ((1ll << (n - i)) - 1) * l * k + F(f[j][id][p + l]));
}
ll ans = 1ll << 60;
rep(i, 0, N - 1) ans = min(ans, g[1][i]);
wr(ans), putchar('\n');
}
signed main() {
t = rd(), n = rd(), k = rd();
memcpy(pre[1].a + 1, p + 1, k << 2);
rep(i, 2, fac[k]) pre[i] = pre[i - 1], next_permutation(pre[i].a + 1, pre[i].a + k + 1);
//末尾的 0 表示更高的若干数
q.push((sta) {
vector<int>(pre[1].a + 1, pre[1].a + k + 2), {}, {}, 0, 0
});
q.front().work();
while (q.size()) {
sta u = q.front(), v;
q.pop();
rep(i, 0, 2) if (!u.a[i].empty()) rep(j, 0, 2) if (i != j && (u.a[i].back() == 0 || (u.a[j].empty() || u.a[j].back() > 0))) {
v = u;
v.a[j].push_back(v.a[i].back());
(v.a[i].back() ? v.y : v.x)++;
v.a[i].pop_back();
if (v.work()) q.push(v);
}
}
int a[6];
memcpy(a, p, sizeof a);
memset(tr, 10, sizeof tr);
rep(j, 1, fac[k])
rep(i, 0, N - 1) {
auto it = mp[i].find({{}, {}, vector<int>(pre[j].a + 1, pre[j].a + k + 2)});
if (it != mp[i].end()) tr[i][j] = it->second;
}
rep(i, 1, fac[k])
rep(j, 1, fac[k])
mul[i][j] = (pre[i] * pre[j]).getid();
//背包
memset(f, 10, sizeof f);
rep(i, 1, fac[k]) rep(j, 0, N - 1) f[1][i][j] = tr[j][i];
rep(i, 1, N - 1)
rep(j, 1, fac[k])
rep(l, 1, N - 1)
rep(r, 0, N - 1 - l)
rep(p, 1, fac[k])
f[i + 1][mul[j][p]][l + r] = min(f[i + 1][mul[j][p]][l + r], f[i][j][l] + tr[r][p]);
while (t--) {
rep(i, 1, n) ::a[i].in();
solve();
if (t) n = rd(), k = rd();
}
return 0;
}
```