XF 换根
sLMxf
·
·
算法·理论
0. 背景
换根 DP,有许许多多的恶心题。
然而有一种可以解决大部分换根 DP 的操作:记忆化搜索。虽然叫 XF 换根,但与换根没有关系。
1. XF 换根
1.0 介绍
XF 换根是由 @sLMxf 和 @General0826 自主研发的算法。
本算法的核心在于:不需要推式子;又或者在对子树的选择个数或顺序无要求的情况下,可以优化到 O(n);又或者解决一些无法换根的问题。(可以发现,XF 换根能做的换根一定能做,但换根能做的 XF 换根不一定能做)
1.1 导入
例题:P3478 [POI 2008] STA-Station
1.1.0 换根
不是都来看 blog 了连换根都不会。
自己抄题解去吧。
1.1.1 朴素的 DP
我们考虑重新定义。定义 dp_x 表示以 x 为根的答案。
不难发现,dp_x=\sum\limits_{v\in son_x}(dp_v+siz_v)+1。
void dfs(int x,int fa)
{
dp[x]=siz[x]=1;
for(int v:G[x])
{
if(v==fa) continue;
dfs(v,x);
dp[x]+=dp[v]+siz[v];
siz[x]+=siz[v];
}
}
1.1.2 优化
我们对其进行使用记忆化搜索。
重新定义状态 dp_{x,fa} 表示当 \mathbf x 的父亲为 \mathbf {fa} 时,此时的答案。
状态转移方程不变:
dp_{x,fa}=\sum\limits_{\substack{v\in nbr_x\\v\ne fa}}(dp_{v,x}+siz_v)+1
然后就可以了。
1.2 代码实现
1.2.1 数组法
只针对于 O(n^2) 可过的情况下,比如 这道题,可以参考题解。
1.2.2 map 法
考虑建立 O(n) 个 map,这样使用就非常方便。
调用时直接查询即可。
:::success[XF 换根:map 法]
vector<signed> G[1000008];
unordered_map<signed,int> dp[1000008];
unordered_map<signed,signed> siz[1000008];
void dfs(int x,int fa)
{
if(siz[x].find(fa)!=siz[x].end()) return ;
int Dp=1,Siz=1;
for(int v:G[x])
{
if(v==fa) continue;
dfs(v,x);
Dp+=dp[v][x]+siz[v][x];
Siz+=siz[v][x];
}
dp[x][fa]=Dp;
siz[x][fa]=Siz;
}
:::
1.2.3 vector 法
就像存图上每个点的邻居一样,我们同时存储 dp 数组和 siz 数组。
但是这样存储有一个小问题,就是不好快速寻找 x 在 y 的邻居数组中的位置。
但这个问题很好解决,在建边时顺便存储。
:::success[XF 换根:vector 实现]
void dfs(int x,int fa,int w)
{
if(w!=-1&&SIZ[x][w]) return ;
int dp=1,siz=1,Dp,Siz;
for(int i=0;i<G[x].size();i++)
{
if(G[x][i]==fa) continue;
dfs(G[x][i],x,W[x][i]);
Dp=DP[G[x][i]][W[x][i]],Siz=SIZ[G[x][i]][W[x][i]];
if(w==-1)
{
sum+=Dp+Siz;
}
else
{
dp+=Dp+Siz;
siz+=Siz;
}
}
if(w!=-1)
{
DP[x][w]=dp;
SIZ[x][w]=siz;
}
}
// 以上为 dfs
// 以下为输入
for(int i=1;i<n;i++)
{
int a,b;
cin>>a>>b;
G[a].emplace_back(b);
G[b].emplace_back(a);
W[a].emplace_back(G[b].size()-1);
W[b].emplace_back(G[a].size()-1);
DP[a].emplace_back(0);
DP[b].emplace_back(0);
SIZ[a].emplace_back(0);
SIZ[b].emplace_back(0);
}
:::
可以用 resize 优化。
1.2.4 链式前向星优化
将 vector 改成链式前向星即可。
当然,推荐大家开个结构体,不然比较丑。(但是我写的就挺丑的)
:::success[XF 换根:链式前向星]
struct node{
int v,nxt;
}e[N*2];
struct xf{
bool vis;
long long dp;
int siz,w;
}cc[N*2];
void add(int u,int v)
{
tot++;
e[tot].nxt=head[u];
e[tot].v=v;
head[u]=tot;
tot++;
e[tot].nxt=head[v];
e[tot].v=u;
head[v]=tot;
cc[tot-1]={0,0,0,tot};
cc[tot]={0,0,0,tot-1};
}
int dp[N],siz[N],cnt=0,sss=0;
void dfs(int x,int fa,int w)
{
if(!w)sss++;
if(w&&cc[w].vis)
{
dp[x]=cc[w].dp,siz[x]=cc[w].siz;
return ;
}
cc[w].vis=1;
siz[x]=dp[x]=1;
for(int i=head[x];i;i=e[i].nxt)
{
int v=e[i].v;
if(v==fa) continue;
dfs(v,x,cc[i].w);
dp[x]+=dp[v]+siz[v];
siz[x]+=siz[v];
}
cc[w].dp=dp[x];
cc[w].siz=siz[x];
return ;
}
:::
1.3 时间复杂度
一个点,设其度数为 k,则他会有 k 次进入这个点,每次需要转移 k-1 次。时间复杂度 O(k(k-1))。
那么总的时间复杂度为 O(\sum d_i^2),其中 d_i 为度数。
卡 XF 换根的最简单的办法就是菊花图。
当然呢,XF 换根随机图上还是飞起来的。
2. 优化
2.1 优化过程
在刚刚给出的例题中,我们使用了 XF 换根获得了 95\text{pts} 的高分,但是仍然没有获得满分。
如何得到满分?
@General0826:建立虚拟节点
例如,对于如图的结点 1:
考虑建立虚拟节点 6,7:
注意到建立了一棵二叉树后,所有点的度数 \le 3。那么此时再使用 XF 换根,尽管时间复杂度不变,但是运行时间可控。
分析可得:最多建立 O(n) 个虚拟结点,时间复杂度接近 O(2n\times 2\times 3)=O(12n)=\mathbf{O(n)}!!!
所以到底如何实现?
首先如何去建立虚拟节点?
其实很简单,每次拿 x 的两个儿子 u,v(它们也可能是虚拟节点),新建虚拟节点 w,连接 u,w 和 v,w 即可。最后两个儿子直接向 x 连边。
建立虚拟节点后,如果我们直接无视掉虚拟节点,那么 5\to 3 的路经长度会变为 1。
所以正确的想法应该是:虚拟节点与其父亲的连边为虚边。不难证明,此想法正确。如图,1\to 3 长度为正确的 1,5\to 3 长度为正确的 2。
请注意,1,6,7 本质仍然为 1 个点,DP 时应该选择其中深度最小的计算。
你也可以认为同一个 scc 内为虚边连接,不同 scc 实边相连。
2.2 复杂度分析
假设我们建立 x 叉树,不难建立函数关系式 y=\left(\frac{1}{x-1}+1\right)x\cdot\left(x+1\right)\left\{x>1\right\}
这是函数图像。
当然大家肯定也不好分析,给出结论:x=2 最优,其次为 x=3。
---
对于空间,我们多出了一倍空间,$x=3$ 时,常数为 $3$ 倍;$x=2$ 时,常数为 $4$ 倍。
---
以上分析皆为估计,有误请私信。
## 2.3 代码实现
我们仍然以 [P3478 [POI 2008] STA-Station](https://www.luogu.com.cn/problem/P3478) 为例题来实现。
下面的代码小心食用,本人代码常数大,写出来也挺丑。
:::success[XF 换根:P3478 [POI 2008] STA-Station]
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+6;
int head[N],tot=0,total,n,vit[N];
vector<int>son;
struct node{
int v,nxt;
bool vit;
}e[N*2];
struct xf{
bool vis;
long long dp;
int siz;
}cc[N*2];
vector<int>G[N];
void add(int u,int v,int x=0)
{
tot++;
e[tot].nxt=head[u];
e[tot].v=v;
e[tot].vit=((u<=n&&v<=n)||x);
head[u]=tot;
tot++;
e[tot].nxt=head[v];
e[tot].v=u;
e[tot].vit=((u<=n&&v<=n)||x);
head[v]=tot;
}
long long dp[N],siz[N];
void make_vit(int x,int fa)
{
son.clear();
int cnt=0;
for(int v:G[x])
if(v!=fa)
son.push_back(v),cnt++;
if(cnt==0) return ;
if(cnt<=2)
{
add(x,son[0]);
if(cnt>1) add(x,son[1]);
for(int v:G[x]) if(v!=fa) make_vit(v,x);
return ;
}
int rt=son[0],florr=1;
for(int i=1;i<cnt;i++)
{
if(cnt-1==i) break;
total++;
add(total,rt,florr);
add(total,son[i],1);
florr=0;
rt=total;
}
if(rt==son[cnt-1])
add(x,rt);
else
{
add(x,rt);
add(x,son[cnt-1]);
}
for(int v:G[x]) if(v!=fa) make_vit(v,x);
}
void dfs(int x,int fa,int w)
{
if(w&&cc[w].vis)
{
dp[x]=cc[w].dp;
siz[x]=cc[w].siz;
return ;
}
cc[w].vis=1;
siz[x]=dp[x]=vit[x];
for(int i=head[x];i;i=e[i].nxt)
{
int v=e[i].v;
if(v==fa) continue;
dfs(v,x,i);
dp[x]+=dp[v]+siz[v]*e[i].vit;
siz[x]+=siz[v];
}
cc[w].dp=dp[x];
cc[w].siz=siz[x];
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int u,v,p=0;
long long ans=0;
cin>>n;
for(int i=1;i<=n;i++) vit[i]=1;
for(int i=1;i<n;i++)
{
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
total=n;
make_vit(1,0);
for(int i=1;i<=n;i++)
{
dfs(i,0,0);
if(ans<dp[i])
{
ans=dp[i];
p=i;
}
}
cout<<p<<'\n';
return 0;
}
```
:::
> @[General0826](/user/1351126):@[sLMxf](/user/752953) 你的代码长度怎么大大的。
:::success[XF 换 Gen]
```cpp
#include<bits/stdc++.h>
#define int long long
#define mid (L+R>>1)
using namespace std;
const int N=4e6+5;
int to[N],head[N],nxt[N],tot=1,meg[N],ror;
int vis[N],len,n,x,y;
vector<int>c[N];
int siz[N],sum[N],ans=1e9;
void add(int x,int y,bool flag){
to[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
vis[tot]=flag;
to[++tot]=x;
nxt[tot]=head[y];
head[y]=tot;
vis[tot]=flag;
}
int build(int L,int R){
if(L==R) return meg[L];
int dx=++ror;
add(dx,build(L,mid),L==mid);
add(dx,build(mid+1,R),mid+1==R);
return dx;
}
void init(int u,int lst){
for(int i=0;i<c[u].size();i++){
int v=c[u][i];
if(v==lst) continue;
init(v,u);
}
len=0;
for(int i=0;i<c[u].size();i++)
if(c[u][i]!=lst)
meg[++len]=c[u][i];
if(len!=0)
add(u,build(1,len),1==len);
}
void dfs(int u,int id){
if(sum[id]!=-1) return ;
siz[id]=(u<=n);
sum[id]=0;
for(int i=head[u];i;i=nxt[i]){
if((i^1)==id) continue;
dfs(to[i],i);
siz[id]+=siz[i];
sum[id]+=sum[i];
if(vis[i])
sum[id]+=siz[i];
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
ror=n;
for(int i=1;i<n;i++){
cin>>x>>y;
c[x].push_back(y);
c[y].push_back(x);
}
init(1,0);
memset(sum,-1,sizeof(sum));
int op=0,ans=0;
for(int i=1;i<=n;i++){
sum[0]=-1;
dfs(i,0);
if(ans<sum[0]){
op=i;
ans=sum[0];
}
}
cout<<op;
return 0;
}
```
:::
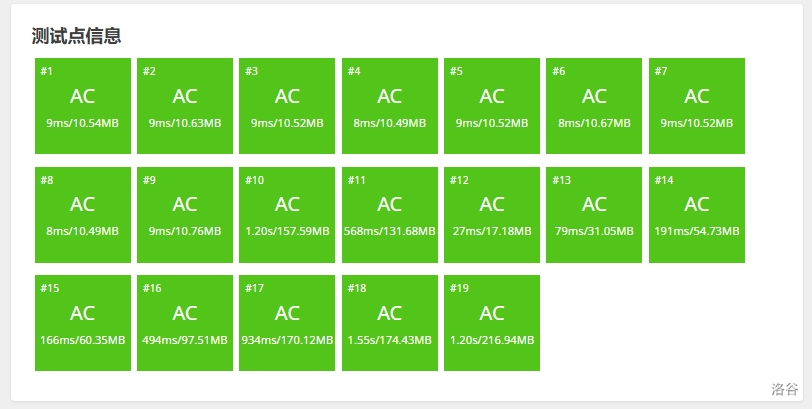
## 2.4 实现比较
#### XF 换根
#### 普通换根
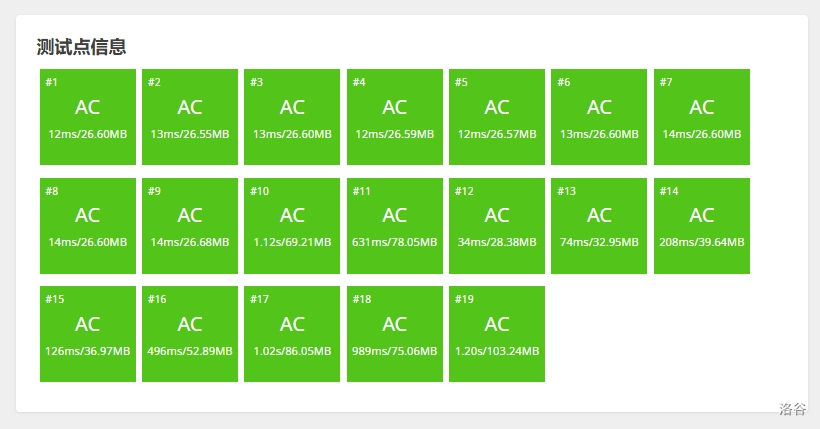
除了空间二倍,时间差不太多。
## 2.5 注意要点
1. 只有虚点和父亲的连边才为虚边。
2. 我们优化的本质是“放点”(也就是将“缩点”反过来),请注意计算时我们“放出来的点”其实是深度最浅的点。
# 3. XF 换根利弊分析
不难发现,此算法优化前,时间复杂度存在问题;优化后空间翻二倍,但是无法处理子树的选择、排序等问题。
~~但是后两类问题真的会有换根题目吗,可能有但我太弱了。~~
但是,优化前针对随机数据(如 CCF 数据)具有不错的性质,优化后我也不知道有什么用。
# 4. 例题解剖
## 4.1 [P3478 [POI 2008] STA-Station](https://www.luogu.com.cn/problem/P3478)
不是我哪里没讲清楚了。
## 4.2 [P6419 [COCI 2014/2015 #1] Kamp](https://www.luogu.com.cn/problem/P6419)
本题本来还是有点难度的,但在 XF 换根面前也不过是模板题罢了。
定义 $dp_x$ 表示以 $x$ 为根的子树答案,不难发现:
$$dp_x=\sum_{v\in son_x}[dp_v>0](dp_v+2w_{x\to v})$$
最后对答案减去一个最长链。
使用 XF 换根,优化之 $O(n)$ 即可。
## 4.3 [P13248 [GCJ 2014 #1A] Full Binary Tree](https://www.luogu.com.cn/problem/P13248)
数据很小,可以使用数组法。
## 4.4 [P6584 重拳出击](https://www.luogu.com.cn/problem/P6584)
咋了不就是 XF 换根板子吗。
枚举小 Z 最后跑到哪里去就可以了。
## 4.5 [【模板】XF 换根](https://www.luogu.com.cn/problem/U531539)
注意最浅的点。