解题报告P1737 [NOI2016]旷野大计算

紫钦 · 2019-12-26 01:23:48 · 题解

题目链接：P1737 [NOI2016]旷野大计算。

题目大意：只允许使用加、取反（添负号）、偏移（加减一个常数）、左右移位（乘或除以 2 的非负整数次幂）和神奇的 S(x) 函数来进行编程，~~造一台计算机~~，构造一个计算网络，完成 10 项指定的计算任务。要求计算次数尽可能少。

其中 S(x) 函数为 {\large\frac{1}{1+e^{-x}}} ，是一个非线性的函数。

$y=S(x)$ 的图像： ![](https://cdn.luogu.com.cn/upload/image_hosting/t9az0ugn.png)

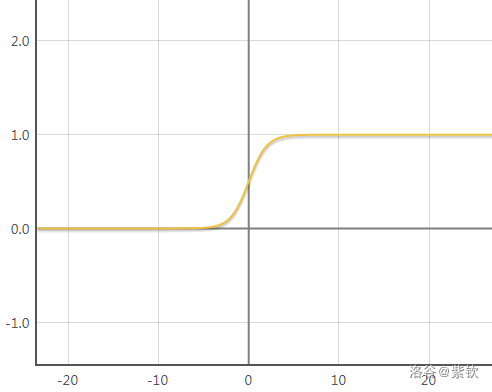
还有三个功能强大但是使用了会扣分的计算节点：比较节点、取两数最大值节点、乘法节点。

是一道提交答案题。

题目补充。

checker下载。

解法：构造答案

具体解法在各个 \text{task} 中介绍。

本题主要就是 10 个计算网络的构造。

核心思想就是：利用好 S(x) 的选择性。用 S(x) 来实现比较大小、取 0 取 1 ，制造分段函数，是这道题的关键所在。

必要的地方加一些小优化，以减少计算节点数。

本题解对解题过程中所用到的所有参数进行了我自认为比较详细地分析，希望这些分析能帮到阅读本题解的你。

\text{task1}

要求

输入：a,b 。

输入限制：|a|,|b|\leqslant10^9 ，小数部分不超过 9 位。

输出：-2a-2b 。

满分行数：6 行。

解决方法

送分点。

一般来说，我们都会想到提取公因数 -2 来减少运算次数。

一般来说，我们也都会想到用左移 1 位来计算乘 2 这个操作。

输出代码

if(n==1) { // 6行。 
    printf("I\n");
    printf("I\n");
    printf("+ 1 2\n");
    printf("< 3 1\n");
    printf("- 4\n");
    printf("O 5");
}

\text{task2}

要求

输入：a 。

输入限制：|a|\leqslant10^9 ，小数部分不超过 9 位。

输出：{\large\frac1{1+e^{17a}}} 。

满分行数：6 行。

解决方法

也是送分点。

观察输出的这个表达式的样子，显然这个点是要用 S(x) 函数的。

然后，注意到 17a=16a+a=2^4a+a ，所以我们可以用位移和加法来解决乘法了。

最后还得小心，S(x)={\large\frac1{1+e^{-x}}} ，还得将 17a 取反后使用 S 函数。

输出代码

if(n==2) { // 6行。 
    printf("I\n");
    printf("< 1 4\n");
    printf("+ 1 2\n");
    printf("- 3\n");
    printf("S 4\n");
    printf("O 5");
}

\text{task3}

要求

输入：a 。

输入限制：|a|\leqslant10^9 ，小数部分不超过 9 位。

输出：\text{sign}(a)=\begin{cases}-1,a<0\\\ \ \ 0,a=0\\\ \ \ 1,a>0\end{cases} 。

满分行数：6 行。

解决方法

不是送分了。开始有难度了。

没有除法，所以 {\large\frac a{|a|}} 泡汤了。况且求 |a| 是下一个 \text{task} 的任务，所以按道理说应该并不容易求。

使用比较语句的话，直接与 0 做比较，输出比较的值即可。可得 6 分。

可以用 a\times2^{-1000} 来造 0 。之后就可以用比较节点比较 a 和 0 的大小。

但是如何使用基本操作来搞出答案呢？

我们是该想想怎么用 S 函数了。

回顾题目

其实，我们在读题面过程中，会发现计算过程中数据精度特别高：小数点后 90 位，整数部分绝对值不超过 10^{1000}。

而最终 Special Judge 判定结果时，只要与标准答案的结果相差小于 10^{-9} 即可。

为什么给如此大的精度？尤其是整数部分，为何那么大？小数部分似乎也精确得过分了，这又是为什么？

而且，为什么 S 函数一定要用 {\large\frac 1{1+e^{-x}}} ？它有什么特殊之处吗？

观察发现，除了第二个测试点需要直接使用了 S(x) 来求出 {\large\frac1{1+e^{17a}}} 精确值之外，其余九个测试点表面上似乎都没有涉及到 S(x) 的使用。

出题人如果只是为了送分的话，为什么还要搞这么一个函数出来呢？这个函数真的没有其他作用了吗？

仔细想想，我们察觉到，好像确实没有哪个测试点需要使用 S(x) 的精确值了。所以，S(x) 的价值，难道是体现在其近似值上面了吗？

种种不同寻常的地方提醒着我们，这道题必然要涉及到极限的问题，即我们要通过某些操作，爆掉 90 位小数的精度，以此模拟取极限的过程。而 S 函数的特殊之处就在于，它在正负无穷大处都有极限，分别为 1 和 0 ，而 y=S(x) 图像上有唯一一个横纵坐标都是有理数的点 (0,{\large\frac12}) ，这也是 S(x) 的性质。进一步的， S(x)+S(-x)=1 ，同样是一条性质。

这就启示我们结合 \lim\limits_{x\to+\infty}S(x)=1 ， \lim\limits_{x\to-\infty}S(x)=0 ，和 S(0)={\large\frac12} 这三条性质，来完成题目。
**所以 $S$ 函数与极限结合，应该是这道题考察的重点之一。**

怎么利用 S 函数呢？

既然要考虑极限，我们很容易想到，将 S 函数乘 2 ，再减去 1，所得恰好是个在 +\infty,-\infty 处极限分别为 +1,-1 的函数（即 {\large\frac2{1+e^{-x}}}-1）。而且在 x=0 处，取值也恰好为 0 。

这么看来，我们应该构造对了。

那么如何取极限？

简单，左移个百来位就可以变得很大了，只要 e^{-x} 爆了 90 位小数的精度，就能认为 S(x) 与 \pm1 精确相等了。

大概多少位比较合适呢？

由 ${\large\frac1{1+e^{-x}}}<1-5\times10^{-91}$ ，得 $e^{-x}<{\large\frac1{1-5\times10^{-91}}}-1$，因为，当 $|x|<1$ 时，根据等比数列求和公式和极限理论，有 ${\large\frac1{1-x}}=1+x+x^2+x^3+\cdots=\sum\limits_{i=0}^{\infty}x^i>1+x$ 。这是因为 $x^2$ 必然是正数，而且比 $x^3$ 大，同理 $x^4$ 是正数，比 $x^5$ 大，以此类推，可知 ${\large\frac1{1-x}}>1+x$ 成立。所以 ${\large\frac1{1-5\times10^{-91}}}-1>5\times10^{-91}$ ，那么，只需要 $e^{-x}<5\times10^{-91}$ 即可。得 $-x<\ln(5\times10^{-91})=\ln5-91\ln10$ ，于是 $x>91\ln10-\ln5\approx207.926$ ，而 $a$ 最小是 $10^{-9}$ ，只需解 $2^k\times10^{-9}>208$ ，解得 $k$ 即可。那么，$k>\log_2(208\times10^9)\approx37.598$ 。所以 $k\geqslant38$ 。
由 ${\large\frac2{1+e^{-x}}}<5\times10^{-91}$ ，得 $e^{-x}>4\times10^{90}-1$ ， $-x>\ln(4\times10^{90}-1)$ ，只需 $-x>\ln(4\times10^{90})$ ，于是 $x<-90\ln10-\ln4\approx-208.619$ ， $k>\log_2(212\times10^9)\approx37.625$ 。

所以，左移 38 位即可。

为什么不用偏移来制造无穷大呢？

因为偏移无法保持正负。
位移有上限，需解方程 2^k\times10^{9}<10^{1000} ，也就是 k<991\log_210\approx3292.031。所以 k=38 没问题的。

输出代码

if(n==3) { // 6行。 
    printf("I\n");
    printf("< 1 38\n");
    printf("S 2\n");
    printf("< 3 1\n");
    printf("C 4 -1\n");
    printf("O 5");
}

\text{task4}

要求

输入：a 。

输入限制：|a|\leqslant10^9 ，小数部分不超过 9 位。

输出：|a| ，即 a 的绝对值。

满分行数：14 行。

解决方法

我的思路和第三个点的差不多。首先我想到，$y=|x|$ 的图像关于 $y$ 轴对称，是个偶函数，而 $S(x)+S(-x)=1$ 告诉我们，$S(x)$ 图像关于 $(0,{\large\frac12})$ 对称。所以，怎么用 $S(x)$ 搞出一个偶函数来？ $S(x)$ 在正负无穷处函数变化率**都**趋于零，这启示我们使用导数。经过验算，我发现，$S'(x)={\large\frac{e^{-x}}{(1+e^{-x})^2}}$ 是个偶函数，且 $\lim\limits_{x\to\infty}S'(x)=0$ ， $S(0)={\large\frac14}$ 。虽然这个导数同 $|x|$ 一样，是个偶函数；但是 $|x|$ 在 $x$ 趋于无穷时是无穷，而 $S'(x)$ 在 $x$ 趋于无穷时却趋于 $0$ 。更糟的是，在 $x=0$ 的两侧，$|x|$ 的表达式可写成不一样的形式，即 $|x|=\begin{cases}\ \ \ x,x>0\\\ \ \ 0,x=0\\-x,x<0\end{cases}$ ，而 $S'(x)$ 不能。所以这样看来， $S'(x)$ 并不能很好的模拟 $|x|$ 函数。即使能够用 $S'(x)$ 构造，怕也免不了一些乘法或者比较的操作。虽然用 $S'(x)$ 直接构造 $|x|$ 的思路失败了，但引入 $S'(x)$ 来辅助解题确实是一个良好的尝试。况且，**难道仅凭这一次尝试，就能断言 $S'(x)$ 毫无作用了吗？** 事实上导数真的很有用。我们用不了 $S'(x)$ 的全部，我们只考虑 $S'(x)$ 在一点处的取值。在解决第三个点时，我们使用了 $S(x)$ 的两个极限，那么做这个点时，不妨再考虑考虑，能不能使用 $S(0)={\large\frac12}$ 这个性质。由 $S'(0)={\large\frac14}$ ，我们很容易写出 $S(x)$ 在 $x=0$ 处的切线：$y={\large\frac14}x+{\large\frac12}$ 。由切线的意义可知，$y=S(x)$ 在 $x=0$ 附近与 $y={\large\frac14}x+{\large\frac12}$ 拟合得很好，这样，我们就得到了一个关于 $x$ 的一次函数，且这个函数减去 ${\large\frac12}$ 再乘 $4$ 就能得到 $x$ 。 > **我们实际上得到的是一个从 $S(x)$ 得到 $x$ 的办法，这个办法很重要。** > > 其重要性在于，我们可以将获得 $x$ 的操作拆解为 $x\to S(x)\to x$ 两个步骤，从而向这两个步骤中添加进一些我们想要的条件。 > > 简言之，这个办法给了我们操作的空间，使得我们有了构造分段函数的可能。更本质的，使得我们有了构造条件语句的可能。所以在这个测试点中，我们要从 $S({\large\frac x{+\infty}})$ 着手构造 $|x|$ （$S({\large\frac x{+\infty}})$ 这种写法不规范，但有助于理解）。现在，再来考虑，如何将 $x$ 的正负区分开来。我们只有找到区分正负的办法，才可能构造出函数来模拟正负有别的 $|x|$ 函数。区分正负的办法上面已经提到了，就是 $S(x)$ 在正负无穷大处的两个极限，分别为 $0,1$ 。那么 $S(-x)$ 的极限就分别为 $1,0$ 。我们要想办法让这两个截然不同的极限对我们构造的函数产生影响，使得我们构造的函数在 $x$ 正负符号不同时具有显著的差别。设这个影响为 $t$ ，把这个影响加到 ${\large\frac {-x}{+\infty}}$ 上去（这就是对我们构造的函数产生影响的操作过程）。现在考虑 $S({\large\frac{-x}{+\infty}}+t)$ 。我们需要让这个影响在 $x>0$ 时为无穷小（即：几乎没什么影响），在 $x<0$ 时足够大，大到能显著影响 $S({\large\frac{-x}{+\infty}}+t)$ 的值。所谓显著影响 $S({\large\frac{-x}{+\infty}}+t)$ 的值，无非就是把 $S({\large\frac{-x}{+\infty}})$ 的值从 ${\large\frac12}$ 附近变成 $1$ ，就是说 $S({\large\frac{-x}{+\infty}}+t)\to1$ 。而减去 ${\large\frac12}$ 再乘 $4$ 后，这个影响作用的结果就变成了“使 $0$ 变成 $2$ ”。这说明 $t$ 应该是个由 $1$ 搞出来的无穷大。比方说 $1\times2^{64}$ （这里未必就是 $64$ 这个数，还可以更大，而且这里的 $1$ 不是确切的数字 $1$ ，它只是表示一个趋近于 $1$ 但永远不等于 $1$ 的变量）。我们把这个大小为 $2$ 的影响稍微调整一下，通过位移**调整到**和原来的影响 $t$ 大小相当的地步。这样，我们就可以通过减去 $t$ 来消除多余的影响，来构造出一个在 $x<0$ 时取 $0$ ，$x>0$ 时取 $x$ 的函数。即 $\begin{cases}0,x<0\\x,x>0\end{cases}$ 。这下就好办了。让这个函数乘 $2$ ，再减去 $x$ ，就得到 $|x|$ 啦！上面的思考太抽象了，我们来重新整理一下思路： + 首先，计算 $t=S(-x\times2^{q})\times2^{p}=\begin{cases}0\ \ ,x>0\\2^p,x<0\end{cases}$ ， $PS.$ 这是 $y=S(x\times2^{41})\times2^{178}$ 的图像： ![](https://cdn.luogu.com.cn/upload/image_hosting/4judcfh2.png) 这里就要求 $S(-x\times2^q)$ 能够与 $0$ 或 $1$ 近似相等， + 于是令 $x=-10^{-9}$ ，只需有 ${\large\frac1{1+e^{-2^q10^{-9}}}}>1-10^{-90}$ ，利用上面的近似公式，可知 $1-e^{-2^q10^{-9}}<{\large\frac1{1+e^{-2^q10^{-9}}}}$ ，只需要 $1-e^{-2^q10^{-9}}>1-10^{-90}$ ，即 $2^q10^{-9}>90\ln10$ ，即 $q>\log_2(9\times10^{10}\ln10)\approx37.59$ ，所以 $q\geqslant38$ 。 + 再令 $x=10^{-9}$ ，只需有 ${\large\frac1{1+e^{2^q10^{-9}}}}<10^{-90}$ ，即 $e^{2^q10^{-9}}>10^{90}-1$ ，只需 $e^{2^q10^{-9}}>10^{90}$ ，即 $2^q10^{-9}>90\ln10$ ，与上种情况同解，所以 $q\geqslant38$ 。这样，在跳蚤看来，$S(-x\times2^q)$ 与 $0$ 或 $1$ 是精确相等的。 $PS.$ 这是 $y=S(x\times2^{41})$ 的图像： ![](https://cdn.luogu.com.cn/upload/image_hosting/nbm41bur.png) + 然后，计算 $S({\large\frac{-x}{2^{k}}}+t)=\begin{cases}{\large\frac14}{\large\frac{-x}{2^{k}}}+{\large\frac12},x>0\\\\1\ \ \ \ \ \ \ \ \ \ \ \ \ ,x<0\end{cases}$ ， *** **声明：为了方便书写，以下所有表达式 $x$ 均表示取反后的 $x$ ，但表达式中表示条件的 $x$ 仍然为未取反的 $x$ 。** **声明：为了方便书写，以下所有表达式 $x$ 均表示取反后的 $x$ ，但表达式中表示条件的 $x$ 仍然为未取反的 $x$ 。** **声明：为了方便书写，以下所有表达式 $x$ 均表示取反后的 $x$ ，但表达式中表示条件的 $x$ 仍然为未取反的 $x$ 。** *** + 这里要求 $x>0$ 时， $({\large\frac14}{\large\frac x{2^{k}}}+{\large\frac12})-S({\large\frac x{2^{k}}})<10^{-90}$ ，不妨取 $x=10^9$ ，即 ${\large\frac{10^9}{4\times2^k}+{\large\frac12}-{\large\frac1{1+e^{-2^{-k}10^9}}}}<10^{-90}

为了方便书写，设 ${\large\frac{10^9}{2^k}}=t$ ，

则上式为 ${\large\frac{t}{4}}+{\large\frac12}-{\large\frac1{1+e^{-t}}}<10^{-90}$

即 ${\large\frac{t}{4}}-{\large\frac{1-e^{-t}}{2(1+e^{-t})}}<10^{-90}$ ，

即 ${\large\frac{t}{2}}-{\large\frac{e^{t}-1}{e^{t}+1}}<2\times10^{-90}$ ，

因为 $t>0$ 时， ${\large\frac{e^{t}-1}{e^{t}+1}}>{\large\frac{t}{e^t+1}}$ ，

> 这里用到了不等式 $e^t>t+1$ ，该不等式可用导数的相关知识来证明。

所以只需 ${\large\frac{t}{2}}-{\large\frac{t}{e^t+1}}<2\times10^{-90}$ ，

即 $t{\large\frac{e^t-1}{2(e^t+1)}}<2\times10^{-90}$ ，

因为 $t>0$ 时， ${\large\frac{1}{(e^t+1)}}<{\large\frac{1}{2}}$ ，

所以只需 ${\large\frac{t(e^t-1)}{4}}<2\times10^{-90}$ ，即 $t(e^t-1)<8\times10^{-90}$ ，

还是利用 $e^t>t+1$ ，欲使上式成立，至少需要满足 $(e^t-1)^2<8\times10^{-90}$ ，

解得 $t<\ln(2\sqrt2\times10^{-45}+1)$ ，

（其实只是个必要条件）

把 $t={\large\frac{10^9}{2^k}}$ 代入，得 ${\large\frac{10^9}{2^k}}<\ln(2\sqrt2\times10^{-45}+1)$ ，

即 $2^{k}>{\large\frac{10^9}{\ln(2\sqrt2\times10^{-45}+1)}}$ ，

即 $k>9\log_210-\log_2(\ln(2\sqrt2\times10^{-45}+1))\approx177.884$ ，

所以 $k\geqslant178$ 。

当然 $k$ 不能取太大，否则会造成 ${\large\frac{x}{2^k}}$ 的精度下降，只需 $10^{-9}>2^k\times10^{-90}$ ，解得 $k\leqslant269$ 。

而且，我所采用的放缩方式，其放缩幅度还是很大的，所以 $178$ 的下界很松。但上界 $269$ 是严格的。

这里还要求 x<0 时， {\large\frac1{1+e^{-2^p}}}>1-10^{-90} ，

只需 1-e^{-2^p}>1-10^{-90} ，

即 p>\log_2(90\ln10)\approx7.695 ，

至于 {\large\frac{x}{2^k}} ，它很小，只要 2^p 够大，它对 2^p 的影响就不足以改变 S({\large\frac x{2^{k}}}+t) 的值。

所以 p\geqslant8 。
其实没必要要求计算所得的数在 90 位小数内精确相等，只要保证计算结果的 9 位小数是正确的，就能解决这个问题。

而我保证了 90 位小数范围内精确相等，也是为了避免之后左移操作造成极大的误差。所以也不无道理。

不过我的推理过程中有一些放缩幅度是较大的，并不能恰好取到阈值。而且我分析的时候并没有考虑小数点 90 位后是四舍五入的。所以我的取值基本上能做到功过相抵。当然你想要考虑四舍五入也可以，这个的证明就要靠读者自己发挥啦，可以参考上面的过程。

我写这么一大篇数学推理就是为了告诉读者这些参数该如何取。每个参数都是有理论依据的，而不是随便取一些足够大或足够小的数就行。即便随便取参数会更快，但我更推荐从数学上得到验证。

接着，减去二分之一 S({\large\frac x{2^{k}}}+t)-{\large\frac12}=\begin{cases}{\large\frac14}{\large\frac x{2^{k}}},x>0\\\\{\large\frac12}\ \ \ \ \ ,x<0\end{cases} ，
再然后，乘 2^{k+2} ，得 (S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+2}=\begin{cases}x\ \ \ \ \ ,x>0\\2^{k+1},x<0\end{cases} ，
接着，减去 t 的影响，得 (S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+2}-t=\begin{cases}x\ \ \ \ \ \ \ \ \ \ \ ,x>0\\2^{k+1}-t,x<0\end{cases}

我们要求 2^{k+1}-t=0 ，而 t=2^p,(x<0) ，所以得到等式 k+1=p 。

所以，(S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+2}-t=\begin{cases}x,x>0\\0,x<0\end{cases} ，

取 q=41,k=178,p=180 ，得到的图像大致为（这里 p=k+2 的原因见下文分析）：
乘 2 再减去 x ，得：
减少计算节点，把 2 乘到里面去，得：
(S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+3}-t\times2-x=\begin{cases}x\ \ \ ,x>0\\-x,x<0\end{cases}
不妨把 p 再取大一点，使 t 不用乘 2 ，

所以取 p=k+2 。式子就变成了：
(S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+3}-t-x=\begin{cases}x\ \ \ ,x>0\\-x,x<0\end{cases}

得到 |x| 啦。

这里面还有一个小问题，那就是 t 在负数和零处的取值是不同的，具体而言 t=S(-x\times2^{q})\times2^{p}\approx\begin{cases}2^{p}\ \ \ ,x<0\\2^{p-1},x=0\\0\ \ \ \ \ \ ,x>0\end{cases} ，这样的话，在 x=0 处计算得到 (S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+3} 后，消除 t 的影响时，需要减去 2t 才行。

但若是特判零的话，势必要增加很多节点，相当麻烦。

我们想到 |x|=\begin{cases}x\ \ \ ,x\geqslant0\\-x,x<0\end{cases} ，所以我们能不能把 x=0 和 x>0 合并到一起运算呢（或者和 x<0 合并到一起运算）？

可以的。

那么，怎么合并呢？

由于 x 小数部分不超过 9 位，所以给 x 加上一个很小的常数 \varepsilon=10^{-10} 即可。这样，当 x\neq0 时， x 原本的符号不改变；x=0 时，x 变成了正数 10^{-10}。

相应的我们需要调整一下参数，

此时需要满足 q>\log_2(9\times10^{11}\ln10)\approx40.914 ，

所以 q\geqslant41 。

> $PS.

$2^{40.914}\approx2,071,768,581,099.5056016$ 。差距还是蛮大的。

我们不妨取 q=41,k=178,p=180 。

这样一写，发现至少要 15 行，究其原因，是我们需要对 x,t 各做一次取反。所以考虑不对 x,t 取反，而对 (S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+3} 取反的写法。

声明到此结束。

令 t=S({\large\frac{x+\varepsilon}{2^q}})\times2^p=\begin{cases}2^p,x\geqslant0\\0\ \ ,x<0\end{cases} ，我们容易得到，答案就是：

这样就只需要取一次反，恰好 $14$ 行。 ## 输出代码 $6$ 分代码，使用乘法节点： ```cpp if(n==4) { // 6分代码。 printf("I\n"); printf("< 1 38\n"); printf("S 2\n"); printf("< 3 1\n"); printf("C 4 -1\n"); printf("* 1 5\n"); printf("O 6"); } ``` $9$ 分代码，$15$ 行： ```cpp if(n==4) { // 15行。 printf("I\n"); printf("C 1 0.0000000001\n"); printf("- 2\n"); printf("< 3 41\n"); printf("S 4\n"); printf("< 5 180\n"); printf("> 1 178\n"); printf("+ 7 6\n"); printf("S 8\n"); printf("C 9 -0.5\n"); printf("< 10 181\n"); printf("- 6\n"); printf("+ 12 11\n"); printf("+ 13 3\n"); printf("O 14"); } ``` 以及满分代码，$14$ 行： ```cpp if(n==4) { // 14行。 printf("I\n"); printf("C 1 0.0000000001\n"); printf("< 2 41\n"); printf("S 3\n"); printf("< 4 180\n"); printf("> 1 178\n"); printf("+ 6 5\n"); printf("S 7\n"); printf("C 8 -0.5\n"); printf("< 9 181\n"); printf("- 10\n"); printf("+ 11 5\n"); printf("+ 12 1\n"); printf("O 13"); } ``` # $\text{task5}

要求

输入：a_1,a_2,\cdots,a_{32}

输入限制：a_1,a_2,\cdots,a_{32}\in\{0,1\} 。

输出：把 a_1,a_2,\cdots,a_{32} 从左到右看成一个二进制整数，高位在左，低位在右，输出该整数的值。

满分行数：95 行。

解决方法

终于，

熬过上题后，

再一次遇到送分点。

按照位数加权再相加即可。

只要弄对行数，就没有任何问题。

显然没有更优解。因为没有能合并的项。

秦九韶算法可减少乘法次数，但现在是做位移。

输出代码

if(n==5) { // 95行。 
    for(int i=1;i<=32;++i) printf("I\n");
    for(int i=1;i<=31;++i) printf("< %d %d\n",i,32-i);
    printf("+ 63 32\n");
    for(int i=64;i<=93;++i) printf("+ %d %d\n",i,i-31);
    printf("O 94");
}

\text{task6}

要求

输入：a 。

输入限制：0\leqslant|a|<2^{32} ，a 为整数。

输出：输出 32 个整数，从高位到低位输出 a 的二进制表示（不足 32 位的在高位补 0）。

满分行数：190 行。

解决方法

输出的是 a 的二进制表示，肯定只包含 0 和 1 。

可以想到，这题又要用 S(x) 函数来搞出 0 和 1 。

用 S(x) 获得 0 和 1 要求自变量 x 有正负两种取值，所以我们构造这个正负的取值。

考虑 a 的 2 进制的最高位，即第 31 位，很显然，若这一位为 1 ，则 a\geqslant2^{31} ；若这一位为 0 ，则 a<2^{31} ，于是我们减去 2^{31} 就能搞出正负不同的取值了。

同样的，我们需要加上 10^{-10} 来保证 S(x) 不会恰好取到 {\large\frac12} 。

由此我们发现，S(x) 函数能够用来比较变量和某个常数之间的大小关系。

我们至少需要将减去 2^{31} 后的数左移 41 位以爆掉精度。这是 \text{task4} 中计算过的。

所以我们计算最高位时就输出 S((a-2^{31})\times2^{41}) ，即 S(a\times2^{41}-2^{72}) 。

我们得到 0 或 1 后，把它左移恰当位数后再从原数中减去，得到 a' ，就可以继续对下一位搞出正负两种取值了。第二高位答案就是 S((a'-2^{30})\times2^{41})=S(a'\times2^{41}-2^{71}) 。

诶？还是乘 41 哎！

于是我们发觉，可以一开始就将 a 左移 41 位，以减少计算节点数。

但这样搞就需要我们计算出 2^{42} 到 2^{72} 这 31 个幂次方了。计算这些幂次方可以用高精（三个 long\ long 拼起来就足够了），可以用 pow 函数，也可以用计算器来手动模拟压位高精。

当然最靠谱的方法就是用题目提供的 checker 来计算。写好计算节点，输入 1 ，让 checker 自己跑出来 2^{42} 到 2^{72} 。省时省力。

总之是可以预处理的。

总体思路大概就是这样了。

然后发现，我们可以把“加上 10^{-10}” 这个操作放到一开始，这样就不必每次循环都多使用一个计算节点了。

计算一下节点的总数，循环里至少需要 “C,S,O,-,<,+” 六个节点，把最后一位拿出来直接处理的话，就只需要 31 次循环。

满分行数是 190 ，恰好是 31\times6+4 ，所以每次循环用 6 个节点应该确实是正确的。

但我们实际操作一下就会发现，按照以上所说的做法，需要写 191 行，能拿 9 分。

说明有一行可以被优化掉。

仔细想想，发现我们可以把“加上 10^{-10}” 这个操作放到 C 操作里，每次减去的不要刚好是 2 的幂次，而是 2 的幂次减去 10^{-10}\times2^{41}\approx219.902\approx220 ，这样就能减少最开始的偏移节点，从而将计算节点数减少到 190 。

为什么是 2 的幂次减去 220 而不是加上 220 呢？

因为减去 2 的幂次后等于零意味着这一位本来是 1 ，所以我们应该让这一位经过 220 调整完后是个正数。所以应该是 2 的幂次减去 220 。

于是我们把偏移的参数调整一下，通通减去 220 即可。

现在是 190 行。

输出代码

```cpp if(n==6) { // 191行。 char s[32][25]={ "\0", "4398046511104", // 2^42 "8796093022208", // 2^43 "17592186044416", // 2^44 "35184372088832", // 2^45 "70368744177664", // 2^46 "140737488355328", // 2^47 "281474976710656", // 2^48 "562949953421312", // 2^49 "1125899906842624", // 2^50 "2251799813685248", // 2^51 "4503599627370469", // 2^52 "9007199254740992", // 2^53 "18014398509481984", // 2^54 "36028797018963968", // 2^55 "72057594037927936", // 2^56 "144115188075855872", // 2^57 "288230376151711744", // 2^58 "576460752303423488", // 2^59 "1152921504606846976", // 2^60 "2305843009213693952", // 2^61 "4611686018427387904", // 2^62 "9223372036854775808", // 2^63 "18446744073709551616", // 2^64 "36893488147419103232", // 2^65 "73786976294838206464", // 2^66 "147573952589676412928", // 2^67 "295147905179352825856", // 2^68 "590295810358705651712", // 2^69 "1180591620717411303424", // 2^70 "2361183241434822606848", // 2^71 "4722366482869645213696", // 2^72 }; printf("I\n"); printf("C 1 0.0000000001\n"); printf("< 2 41\n"); for(int i=4,j=31;j>=1;--j,i+=6) { printf("C %d -%s\n",i-1,s[j]); printf("S %d\n",i); printf("O %d\n",i+1); printf("- %d\n",i+2); printf("< %d %d\n",i+3,41+j); printf("+ %d %d\n",i+4,i-1); } printf("> 189 41\n"); printf("O 190"); } ``` 满分，$190$ 行： ```cpp if(n==6) { // 190行。 char s[32][25]={ "\0", "4398046510884", // 2^42-220 "8796093021988", // 2^43-220 "17592186044196", // 2^44-220 "35184372088612", // 2^45-220 "70368744177444", // 2^46-220 "140737488355108", // 2^47-220 "281474976710436", // 2^48-220 "562949953421092", // 2^49-220 "1125899906842404", // 2^50-220 "2251799813685028", // 2^51-220 "4503599627370249", // 2^52-220 "9007199254740772", // 2^53-220 "18014398509481764", // 2^54-220 "36028797018963748", // 2^55-220 "72057594037927716", // 2^56-220 "144115188075855652", // 2^57-220 "288230376151711524", // 2^58-220 "576460752303423268", // 2^59-220 "1152921504606846756", // 2^60-220 "2305843009213693732", // 2^61-220 "4611686018427387684", // 2^62-220 "9223372036854775588", // 2^63-220 "18446744073709551396", // 2^64-220 "36893488147419103012", // 2^65-220 "73786976294838206244", // 2^66-220 "147573952589676412708", // 2^67-220 "295147905179352825636", // 2^68-220 "590295810358705651492", // 2^69-220 "1180591620717411303204", // 2^70-220 "2361183241434822606628", // 2^71-220 "4722366482869645213476", // 2^72-220 }; printf("I\n"); printf("< 1 41\n"); for(int i=3,j=31;j>=1;--j,i+=6) { printf("C %d -%s\n",i-1,s[j]); printf("S %d\n",i); printf("O %d\n",i+1); printf("- %d\n",i+2); printf("< %d %d\n",i+3,41+j); printf("+ %d %d\n",i+4,i-1); } printf("> 188 41\n"); printf("O 189"); } ``` # $\text{task7}

要求

输入：a,b 。

输入限制：0\leqslant a,b<2^{32} ， a,b 均为整数。

输出：a,b 按位异或后的结果。

满分行数：605 行。

解决方法

因为是按位异或，所以必然需要把每一位都先取出来。这就用到 \text{task6} 的代码了。

而按位异或完得到的 32 位二进制数还需要转化成十进制数才能输出，所以这又用到 \text{task5} 的代码了。

这就已经用掉大约 2\times5\times31+62=372 个计算节点，满分是 605 个计算节点，所以我们大约需要用 7 个计算节点来完成每一位上的异或操作。

异或还是涉及到 0 和 1 的运算，我们当然离不开 S(x) 函数啦。

自然是要先来研究一下异或操作，看看能不能找到规律。

我们知道：
$0\oplus1=1$ ， $1\oplus0=1$ ， $1\oplus1=0$ ，

考虑做差。

做个差的话， 1\oplus1=0 和 0\oplus0=0 都能正确计算，但 0\oplus1=1\oplus0=1 可能会算出 1,-1 两个值。

怎么把 -1 搞成 1 呢？

取绝对值就好啦。

取绝对值需要 12 个节点，每一位都这样搞，写得再优美也大概需要 700+ 个计算节点。能拿到 8 分。

做差死了吗？

还没，还能抢救一下。

换个思路。我们换个思路，看看还能怎么把 -1 搞成 1 。

设 t 为做差得到的值，即 t=\begin{cases}-1,0\oplus1\\\ \ \ 0,0\oplus0\ or\ 1\oplus1\\\ \ \ 1,1\oplus0\end{cases} ，

首先，怎么把 -1 和 0,1 区分开呢？

简单，加个 0.5 再左移 41 位，再放到 S(x) 里算一下，就得到 u=\begin{cases}0,0\oplus1\\1,0\oplus0\ or\ 1\oplus1\\1,1\oplus0\end{cases} ，

怎么用 u 和 t 搞出异或呢？

我们发现 (1-u)\times2+t=\begin{cases}1,0\oplus1\\0,0\oplus0\ or\ 1\oplus1\\1,1\oplus0\end{cases} 。

得到异或啦。

但这个方法运算过程较麻烦，我们试试将 t 减去 0.5 再左移 41 位，放到 S(x) 里算一下，看看能不能得到更简单的式子。

可以得到 u'=\begin{cases}0,0\oplus1\\0,0\oplus0\ or\ 1\oplus1\\1,1\oplus0\end{cases} ，

进一步的， 2u'-t=\begin{cases}1,0\oplus1\\0,0\oplus0\ or\ 1\oplus1\\1,1\oplus0\end{cases} ，

它显然比上一种方式用的节点少。

于是我们不由得想到，能不能用加法类似实现异或呢？

减法毕竟是“取反+加法”的，计算节点个数严格大于加法，所以如果加法能实现这个操作，就没必要做差了。

幸运的是，加法确实可以。

于是做差真的死了。

考虑做和。

做和的话，0\oplus1=1\oplus0=1 都能正确计算，但是 0+0=0,1+1=2 ，又产生了分歧。

怎么处理分歧呢？
- 首先有一个思路：
考虑到我们的 S(x) 函数现在能比较变量和一个常数的大小关系了，

所以想办法找到一些能用的大小关系，使得 0 和 2 在这些大小关系上表现一致，而 1 却不一致。这样就能区分出 1 和 0,2 了。

设 t=\begin{cases}0,0\oplus0\\1,1\oplus0\ or\ 0\oplus1\\2,1\oplus1\end{cases} ，

我们找两个常数：0.5,1.5 ，0 比他俩都小，2 比他俩都大，1 在他俩中间。

分别减去 0.5 和 1.5 ，再左移 41 位，再放到 S(x) 里算一下，我们看看结果：

设 f_1=S((t-0.5)\times2^{41})=\begin{cases}S(-0.5\times2^{41}) ,0\oplus0\\S(\ \ \ 0.5\times2^{41}),1\oplus0\ or\ 0\oplus1\\S(\ \ \ 1.5\times2^{41}),1\oplus1\end{cases} ，

再设 f_2=S((t-1.5)\times2^{41})=\begin{cases}S(-1.5\times2^{41}) ,0\oplus0\\S(-0.5\times2^{41}),1\oplus0\ or\ 0\oplus1\\S(\ \ \ 1.5\times2^{41}),1\oplus1\end{cases} ，

于是 f_1=\begin{cases}0 ,0\oplus0\\1,1\oplus0\ or\ 0\oplus1\\1,1\oplus1\end{cases} ， f_2=\begin{cases}0 ,0\oplus0\\0,1\oplus0\ or\ 0\oplus1\\1,1\oplus1\end{cases} ，

于是 f_1-f_2=\begin{cases}0 ,0\oplus0\\1,1\oplus0\ or\ 0\oplus1\\0,1\oplus1\end{cases} ，

这样我们就做出异或了。

我开开心心地一写，发现 663 行，能拿 9 分。
*** 换种思路，按照刚刚减法的那个套路来。还是 $t=\begin{cases}0,0\oplus0\\1,1\oplus0\ or\ 0\oplus1\\2,1\oplus1\end{cases}$ ，我们想办法把 $2$ 和 $0,1$ 区分开，方法就是减去 $1.5$ 再左移 $41$ 位，再放到 $S(x)$ 里算一下，得到 $u=\begin{cases}0,0\oplus0\\0,1\oplus0\ or\ 0\oplus1\\1,1\oplus1\end{cases}$ ，观察发现， $t-2u=\begin{cases}0,0\oplus0\\1,1\oplus0\ or\ 0\oplus1\\0,1\oplus1\end{cases}$ ；一样的，若将 $t$ 减去 $0.5$ 再左移、再 $S(x)$ ，得到 $u'=\begin{cases}0,0\oplus0\\1,1\oplus0\ or\ 0\oplus1\\1,1\oplus1\end{cases}$ ，用 $2u'-t=\begin{cases}0,0\oplus0\\1,1\oplus0\ or\ 0\oplus1\\0,1\oplus1\end{cases}$ ，也能用同样多的计算节点得到异或的结果。这种方法比上述 $663$ 行的方法至少少用一个位移节点、一个 $S$ 节点，所以应该是正解了。实测 $603$ 行，可过。

考虑优化。

注意到最终输出的结果是个十进制数，而不是二进制数。我们将 a,b 转化为二进制、做完异或后又转回十进制的过程，是否可以进一步优化呢？

我们知道，其实异或这个操作就是加法的底层实现。

不信你看，就单独的一位二进制位而言，加法有如下规律：
可以看出，就单独的一位而言，加法和异或会得到相同的结果。

但不同的是，在加法中 1+1 会产生进位信号（可以用“与”操作判断是否进位），这个进位信号会被传递给更高一位，从而影响更高一位的值。

所以，如果我们把这个进位信号对更高位的影响消去，就可以把加法操作变成异或操作了。

换句话说，在二进制下考虑，异或就是不进位的加法。

那我们怎么消除进位的影响呢？

先把 a,b 加到一起，

然后还是把每一位都取出来，按位相加。在按位相加的过程中判断进位。

如果某一位上加起来结果等于 2 ，则意味着这一位会向高位进位，而等于 0 或 1 则意味着不会进位。

于是，我们用上文提到的“减去 1.5 再左移 41 位，再放到 S(x) 里算一下”来将“进位”与“不进位”区分开来，得到 u=\begin{cases}0,0\oplus0\\0,1\oplus0\ or\ 0\oplus1\\1,1\oplus1\end{cases} ，即 u=\begin{cases}0,\ \ \ \text{no carry}\\1,\ \ \ \text{carry}\end{cases} ，

若将二进制位从低位到高位编号为 0 到 31 ，则易知第 i 位产生的进位会给第 i+1 位加上 1，所以我们可以通过从 a+b 中减去 1\times2^{i+1} 来消去这个进位的影响。

第 i 位如果不产生进位，那么减去 0\times2^{i+1} 也不会有什么问题。

于是我们可以对上述 603 行代码进行进一步优化了。至少能省去将二进制转化为十进制所用的若干节点。

于是我写了一下，542 行。

将二进制下最低位单独处理，可以再节省 3 个节点。具体而言：
- 取出 a,b 二进制位时，不将最低位右移 41 位还原，而是将其直接减去 1.5\times2^{41} ，再放到 S(x) 里面进行计算。
于是得到了 539 行的计算机。

输出代码

```cpp if(n==7) { // 663行。 char s[32][25]={ "\0", "4398046510884", // 2^42-220 "8796093021988", // 2^43-220 "17592186044196", // 2^44-220 "35184372088612", // 2^45-220 "70368744177444", // 2^46-220 "140737488355108", // 2^47-220 "281474976710436", // 2^48-220 "562949953421092", // 2^49-220 "1125899906842404", // 2^50-220 "2251799813685028", // 2^51-220 "4503599627370249", // 2^52-220 "9007199254740772", // 2^53-220 "18014398509481764", // 2^54-220 "36028797018963748", // 2^55-220 "72057594037927716", // 2^56-220 "144115188075855652", // 2^57-220 "288230376151711524", // 2^58-220 "576460752303423268", // 2^59-220 "1152921504606846756", // 2^60-220 "2305843009213693732", // 2^61-220 "4611686018427387684", // 2^62-220 "9223372036854775588", // 2^63-220 "18446744073709551396", // 2^64-220 "36893488147419103012", // 2^65-220 "73786976294838206244", // 2^66-220 "147573952589676412708", // 2^67-220 "295147905179352825636", // 2^68-220 "590295810358705651492", // 2^69-220 "1180591620717411303204", // 2^70-220 "2361183241434822606628", // 2^71-220 "4722366482869645213476", // 2^72-220 }; char s15[]="3298534883328",s05[]="1099511627776"; printf("I\n"); printf("I\n"); printf("< 1 41\n"); printf("< 2 41\n"); for(int i=5,j=31;j>=1;--j,i+=19) { printf("C %d -%s\n",i-2,s[j]); // i printf("C %d -%s\n",i-1,s[j]); // i+1 printf("S %d\n",i); // i+2 printf("S %d\n",i+1); // i+3 printf("+ %d %d\n",i+2,i+3); // i+4 printf("C %d -0.5\n",i+4); // i+5 printf("C %d -1.5\n",i+4); // i+6 printf("< %d 41\n",i+5); // i+7 printf("< %d 41\n",i+6); // i+8 printf("S %d\n",i+7); // i+9 printf("S %d\n",i+8); // i+10 printf("- %d\n",i+10); // i+11 printf("+ %d %d\n",i+11,i+9); // i+12 printf("- %d\n",i+2); // i+13 printf("- %d\n",i+3); // i+14 printf("< %d %d\n",i+13,41+j); // i+15 printf("< %d %d\n",i+14,41+j); // i+16 printf("+ %d %d\n",i+15,i-2); // i+17 printf("+ %d %d\n",i+16,i-1); // i+18 } printf("+ 592 593\n"); // 594 printf("C 594 -%s\n",s05); printf("C 594 -%s\n",s15); printf("S 595\n"); printf("S 596\n"); printf("- 598\n"); printf("+ 599 597\n"); // 600 for(int i=17,j=31;j>=1;--j,i+=19) printf("< %d %d\n",i,j); // 601~631 for(int i=601,j=631;i<=630;++j,++i) printf("+ %d %d\n",i,j); // 632~661 printf("+ 661 600\n"); printf("O 662"); } ``` 满分，$603$ 行： ```cpp if(n==7) { // 603行。 char s[32][25]={ "\0", "4398046510884", // 2^42-220 "8796093021988", // 2^43-220 "17592186044196", // 2^44-220 "35184372088612", // 2^45-220 "70368744177444", // 2^46-220 "140737488355108", // 2^47-220 "281474976710436", // 2^48-220 "562949953421092", // 2^49-220 "1125899906842404", // 2^50-220 "2251799813685028", // 2^51-220 "4503599627370249", // 2^52-220 "9007199254740772", // 2^53-220 "18014398509481764", // 2^54-220 "36028797018963748", // 2^55-220 "72057594037927716", // 2^56-220 "144115188075855652", // 2^57-220 "288230376151711524", // 2^58-220 "576460752303423268", // 2^59-220 "1152921504606846756", // 2^60-220 "2305843009213693732", // 2^61-220 "4611686018427387684", // 2^62-220 "9223372036854775588", // 2^63-220 "18446744073709551396", // 2^64-220 "36893488147419103012", // 2^65-220 "73786976294838206244", // 2^66-220 "147573952589676412708", // 2^67-220 "295147905179352825636", // 2^68-220 "590295810358705651492", // 2^69-220 "1180591620717411303204", // 2^70-220 "2361183241434822606628", // 2^71-220 "4722366482869645213476", // 2^72-220 }; printf("I\n"); // 1。 printf("I\n"); // 2。 printf("< 1 41\n"); // 3。 for(int i=4,j=31;j>=1;--j,i+=5) { // 4~158。 printf("C %d -%s\n",i-1,s[j]); printf("S %d\n",i); printf("- %d\n",i+1); printf("< %d %d\n",i+2,41+j); printf("+ %d %d\n",i+3,i-1); } printf("> 158 41\n"); // 159。 printf("< 2 41\n"); // 160。 for(int i=161,j=31;j>=1;--j,i+=5) { // 161~315。 printf("C %d -%s\n",i-1,s[j]); printf("S %d\n",i); printf("- %d\n",i+1); printf("< %d %d\n",i+2,41+j); printf("+ %d %d\n",i+3,i-1); } printf("> 315 41\n"); // 316。 for(int i=5,j=1;j<=31;++j,i+=5) { // 317~347。 printf("+ %d %d\n",i,i+157); } printf("+ 159 316\n"); // 348。 for(int i=317,j=1;j<=32;++j,++i) { // 349~380。 printf("C %d -1.5\n",i); } for(int i=349,j=1;j<=32;++j,++i) { // 381~412。 printf("< %d 41\n",i); } for(int i=381,j=1;j<=32;++j,++i) { // 413~444。 printf("S %d\n",i); } for(int i=413,j=1;j<=32;++j,++i) { // 445~476。 printf("< %d 1\n",i); } for(int i=445,j=1;j<=32;++j,++i) { // 477~508。 printf("- %d\n",i); } for(int i=477,j=1;j<=32;++j,++i) { // 509~540。 printf("+ %d %d\n",i,i-160); } for(int i=509,j=31;j>=1;--j,++i) { // 541~571。 printf("< %d %d\n",i,j); } for(int i=540,j=1;j<=31;++j,++i) { // 572~602。 printf("+ %d %d\n",i,i+31); } printf("O 602\n"); } ``` 满分，$542$ 行： ```cpp if(n==7) { // 542行。 char s[32][25]={ "\0", "4398046510884", // 2^42-220 "8796093021988", // 2^43-220 "17592186044196", // 2^44-220 "35184372088612", // 2^45-220 "70368744177444", // 2^46-220 "140737488355108", // 2^47-220 "281474976710436", // 2^48-220 "562949953421092", // 2^49-220 "1125899906842404", // 2^50-220 "2251799813685028", // 2^51-220 "4503599627370249", // 2^52-220 "9007199254740772", // 2^53-220 "18014398509481764", // 2^54-220 "36028797018963748", // 2^55-220 "72057594037927716", // 2^56-220 "144115188075855652", // 2^57-220 "288230376151711524", // 2^58-220 "576460752303423268", // 2^59-220 "1152921504606846756", // 2^60-220 "2305843009213693732", // 2^61-220 "4611686018427387684", // 2^62-220 "9223372036854775588", // 2^63-220 "18446744073709551396", // 2^64-220 "36893488147419103012", // 2^65-220 "73786976294838206244", // 2^66-220 "147573952589676412708", // 2^67-220 "295147905179352825636", // 2^68-220 "590295810358705651492", // 2^69-220 "1180591620717411303204", // 2^70-220 "2361183241434822606628", // 2^71-220 "4722366482869645213476", // 2^72-220 }; printf("I\n"); // 1。 printf("I\n"); // 2。 printf("+ 1 2\n"); // 3。 printf("< 1 41\n"); // 4。 for(int i=5,j=31;j>=1;--j,i+=5) { // 5~159。 printf("C %d -%s\n",i-1,s[j]); printf("S %d\n",i); printf("- %d\n",i+1); printf("< %d %d\n",i+2,41+j); printf("+ %d %d\n",i+3,i-1); } printf("> 159 41\n"); // 160。 printf("< 2 41\n"); // 161。 for(int i=162,j=31;j>=1;--j,i+=5) { // 162~316。 printf("C %d -%s\n",i-1,s[j]); printf("S %d\n",i); printf("- %d\n",i+1); printf("< %d %d\n",i+2,41+j); printf("+ %d %d\n",i+3,i-1); } printf("> 316 41\n"); // 317。 for(int i=6,j=1;j<=31;++j,i+=5) { // 318~348。 printf("+ %d %d\n",i,i+157); } printf("+ 160 317\n"); // 349。 for(int i=318,j=1;j<=32;++j,++i) { // 350~381。 printf("C %d -1.5\n",i); } for(int i=350,j=1;j<=32;++j,++i) { // 382~413。 printf("< %d 41\n",i); } for(int i=382,j=1;j<=32;++j,++i) { // 414~445。 printf("S %d\n",i); } for(int i=414,j=32;j>=1;--j,++i) { // 446~477。 printf("< %d %d\n",i,j); } for(int i=446,j=1;j<=32;++j,++i) { // 478~509。 printf("- %d\n",i); } printf("+ 478 3\n"); // 510。 for(int i=479,j=1;j<=31;++j,++i) { // 511~541。 printf("+ %d %d\n",i,i+31); } printf("O 541"); } ``` 满分，$539$ 行： ```cpp if(n==7) { // 539行。 // (a+b)-sum{(a[i]+b[i]==2)<<i+1} 能省掉二进制转十进制的节点。 char s[32][25]={ "\0", "4398046510884", // 2^42-220 "8796093021988", // 2^43-220 "17592186044196", // 2^44-220 "35184372088612", // 2^45-220 "70368744177444", // 2^46-220 "140737488355108", // 2^47-220 "281474976710436", // 2^48-220 "562949953421092", // 2^49-220 "1125899906842404", // 2^50-220 "2251799813685028", // 2^51-220 "4503599627370249", // 2^52-220 "9007199254740772", // 2^53-220 "18014398509481764", // 2^54-220 "36028797018963748", // 2^55-220 "72057594037927716", // 2^56-220 "144115188075855652", // 2^57-220 "288230376151711524", // 2^58-220 "576460752303423268", // 2^59-220 "1152921504606846756", // 2^60-220 "2305843009213693732", // 2^61-220 "4611686018427387684", // 2^62-220 "9223372036854775588", // 2^63-220 "18446744073709551396", // 2^64-220 "36893488147419103012", // 2^65-220 "73786976294838206244", // 2^66-220 "147573952589676412708", // 2^67-220 "295147905179352825636", // 2^68-220 "590295810358705651492", // 2^69-220 "1180591620717411303204", // 2^70-220 "2361183241434822606628", // 2^71-220 "4722366482869645213476", // 2^72-220 }; char s15[]={"3298534883328"}; printf("I\n"); // 1。 printf("I\n"); // 2。 printf("+ 1 2\n"); // 3。 printf("< 1 41\n"); // 4。 for(int i=5,j=31;j>=1;--j,i+=5) { // 5~159。 printf("C %d -%s\n",i-1,s[j]); printf("S %d\n",i); printf("- %d\n",i+1); printf("< %d %d\n",i+2,41+j); printf("+ %d %d\n",i+3,i-1); } printf("< 2 41\n"); // 160。 for(int i=161,j=31;j>=1;--j,i+=5) { // 161~315。 printf("C %d -%s\n",i-1,s[j]); printf("S %d\n",i); printf("- %d\n",i+1); printf("< %d %d\n",i+2,41+j); printf("+ %d %d\n",i+3,i-1); } for(int i=6,j=1;j<=31;++j,i+=5) { // 316~346。 printf("+ %d %d\n",i,i+156); } printf("+ 159 315\n"); // 347。 for(int i=316,j=1;j<=31;++j,++i) { // 348~378。 printf("C %d -1.5\n",i); } for(int i=348,j=1;j<=31;++j,++i) { // 379~409。 printf("< %d 41\n",i); } printf("C 347 -%s\n",s15); // 410。 for(int i=379,j=1;j<=32;++j,++i) { // 411~442。 printf("S %d\n",i); } for(int i=411,j=32;j>=1;--j,++i) { // 443~474。 printf("< %d %d\n",i,j); } for(int i=443,j=1;j<=32;++j,++i) { // 475~505。 printf("- %d\n",i); } printf("+ 475 3\n"); // 506。 for(int i=476,j=1;j<=31;++j,++i) { // 507~538。 printf("+ %d %d\n",i,i+31); } printf("O 538"); } ``` # $\text{task8}

要求

输入：a 。

输入限制：|a|\leqslant10^9 ，小数部分不超过 9 位。

输出：{\large\frac a{10}} 。

满分行数：7 行。

解决方法

与二进制无关了，所以用不到 S(x) 的选择性了。

通过 node8.ans ，我们知道，满分计算机是 7 个计算节点！

这说明我们需要用一些奇技淫巧了。

能不能二分答案呢？

因为乘 10 的操作还是好做的，所以对 [0,{\large\frac a8}] 进行二分，检验二分值的 10 倍是否等于 a ，用 S(x) 函数来作比较，并完成二分区间的更新。

理论上可行，但二分至误差不超过 10^{-9} 是真的困难，可以预见，我们的计算节点数会多到爆炸。还不如直接用乘法节点赚个实惠。
能不能用多次右移再相加来模拟乘 0.1 的操作呢？

也可以，但仍然不是正解。
0.1=2^{-4}+2^{-5}+2^{-8}+2^{-9}+2^{-12}+2^{-13}+2^{-16}+2^{-17}+2^{-20}+\cdots
而 2^{-4}+2^{-5}+2^{-8}+2^{-9}+2^{-12}+2^{-13}+2^{-16}+2^{-17}+2^{-20}=0.09999942779541015625 ，

只需要加足够多的项就能使得答案在精度范围内准确了。

据说能拿 7 到 8 分。

下面讲正解。

我们考虑如何正确使用 S(x) 函数来完成除以 10 的操作。

回想我们完成 \text{task4} 时对 S(x) 导数的思考，以及我们使用 S(x) 在 x=0 处的切线来获取一条近似直线的操作，

那么我们是否可以找到 S(x) 上一条斜率为 {\large\frac1{10}} 的切线呢？

我们知道， S'(x)={\large\frac{e^{-x}}{(1+e^{-x})^2}}\in(0,{\large\frac14}] ，且 S'(x) 是 R 上的连续函数、偶函数，

所以 \exists\ \xi\in(0,+\infty) ，使得 S'(\xi)={\large\frac1{10}} ，

我们可以写出 S(x) 在这点的切线方程，为 y=S'(\xi)(x-\xi)+S(\xi) ，

即 y={\large\frac1{10}}(x-\xi)+S(\xi) 。

由切线的意义知，当 x 与 \xi 非常接近时，S(x) 近似等于 S'(\xi)(x-\xi)+S(\xi)={\large\frac1{10}}(x-\xi)+S(\xi) ，

所以我们将输入的 a 右移 k 位（造一个微小量），再加上 \xi ，就构造出了一个与 \xi 非常接近的值，并计算 S({\large\frac{a}{2^k}}+\xi) 的值，

因为 {\large\frac{a}{2^k}} 很小，所以 S({\large\frac{a}{2^k}}+\xi) 近似等于 {\large\frac1{10}}({\large\frac{a}{2^k}}+\xi-\xi)+S(\xi)={\large\frac1{10}}{\large\frac{a}{2^k}}+S(\xi) ，

于是 (S({\large\frac{a}{2^k}}+\xi)-S(\xi))\times2^{k} 近似等于 {\large\frac a{10}} 。

好了，现在唯一的问题就是， \xi 等于多少？

解方程 S'(\xi)={\large\frac{e^{-\xi}}{(1+e^{-\xi})^2}}={\large\frac1{10}} ，

得： 10e^{-\xi}=(1+e^{-\xi})^2 ，

得： e^{-2\xi}-8e^{-\xi}+1=0 ，

使用求根公式得： e^{-\xi}=4\pm\sqrt{15} ，

钦定 \xi>0 ，所以 0<e^{-\xi}<1 ，所以舍去 4+\sqrt{15} ，得：e^{-\xi}=4-\sqrt{15} ，

于是 \xi=-\ln(4-\sqrt{15})=\ln(4+\sqrt{15}) ，

于是 S(\xi)={\large\frac1{1+e^{-\xi}}}={\large\frac1{5-\sqrt{15}}}={\large\frac{5+\sqrt{15}}{10}} ，

好了，现在该如何计算出这两个玩意儿？

因为我们最后会乘个 2^k ，所以这两个玩意儿的精度必须极其高才行。

那么先算 k ：

令 x={\large\frac{a}{2^k}} ，

解 {\large\frac1{10}}x+S(\xi)-S(x+\xi)<10^{-90} ，

即 {\large\frac1{10}}x+{\large\frac1{1+e^{-\xi}}}-{\large\frac1{1+e^{-(x+\xi)}}}<10^{-90} ，

即 {\large\frac1{10}}x-{\large\frac{e^{-\xi}-e^{-(x+\xi)}}{(1+e^{-(x+\xi)})(1+e^{-\xi})}}<10^{-90} ，

即 {\large\frac1{10}}x-{\large\frac{e^{x}-1}{(e^{(x+\xi)}+1)(1+e^{-\xi})}}<10^{-90} ，

因为 x>0 时，{\large\frac{e^{x}-1}{(e^{(x+\xi)}+1)(1+e^{-\xi})}}>{\large\frac{x}{(e^{x+\xi}+1)(1+e^{-\xi})}} ，

所以只需 {\large\frac1{10}}x-{\large\frac{x}{(e^{(x+\xi)}+1)(1+e^{-\xi})}}<10^{-90} ，

即 x{\large\frac{(e^{(x+\xi)}+1)(1+e^{-\xi})-10}{10(e^{(x+\xi)}+1)(1+e^{-\xi})}}<10^{-90} ，

注意到 (e^{\xi}+1)(1+e^{-\xi})=4+\sqrt{15}+4-\sqrt{15}+2=10 ，

所以将上式中的 e^{(x+\xi)} 强行拆开，得：x{\large\frac{(e^{(x+\xi)}+1)(1+e^{-\xi})-10}{10(e^{(x+\xi)}+1)(1+e^{-\xi})}}=x{\large\frac{(e^x-1)(e^{\xi}+1)}{10((e^x-1)(e^{\xi}+1)+10)}}<10^{-90}
所以只需 ${\large\frac{(e^x-1)^2(e^{\xi}+1)}{100}}<10^{-90}$ ，即 $x<\ln(\sqrt{(5-\sqrt{15})\times10^{-89}}+1)$ ，把 $x={\large\frac{a}{2^k}}$ 代入得：${\large\frac{a}{2^k}}<\ln(\sqrt{(5-\sqrt{15})\times10^{-89}}+1)
取 a=10^9 ，得 k>9\log_210-\log_2(\ln(\sqrt{(5-\sqrt{15})\times10^{-89}}+1))\approx177.637

故只需 k\geqslant178 。

同样的，k 不能太大，同 \text{task4} ，需有 k\leqslant269 。

同样的，178 这个下界很松。实测取到 86 都没问题。
再来计算：
$S(\xi)={\large\frac1{1+e^{-\xi}}}={\large\frac1{5-\sqrt{15}}}={\large\frac{5+\sqrt{15}}{10}}$ ，怎么算呢？用电脑的计算器计算 $\xi=\ln(4+\sqrt{15})$ ，然后把计算所得的数放到 ```checker``` 里面算出一个 $S(\xi)$ 。 > 不要忘了，你的 ```checker``` 是可以运行你所构造的计算机的。我用电脑的计算器算得 $\xi=$```2.0634370688955605467272811726201``` ，用 ```checker``` 算得 $S(\xi)=$```0.887298334620741688517926539978236773937633025540819832675154107295416657242528255923059519``` ，实测这两个参数可以过。使用强大的计算器算得 $\xi$ 和 $S(\xi)$ 小数点后 $90$ 位（括号里为第 $91$ 位）得： ```2.063437068895560546727281172620131871456591449883392499836032692765902842847409911780353006(4)``` ```0.887298334620741688517926539978239961083292170529159082658757376611348309193697903351928737(6)``` $PS.$ 可以看到，还是有一定的误差的。这是 $y=(S({\large\frac{x}{2^{178}}}+\xi)-S(\xi))\times2^{178}$ 的图像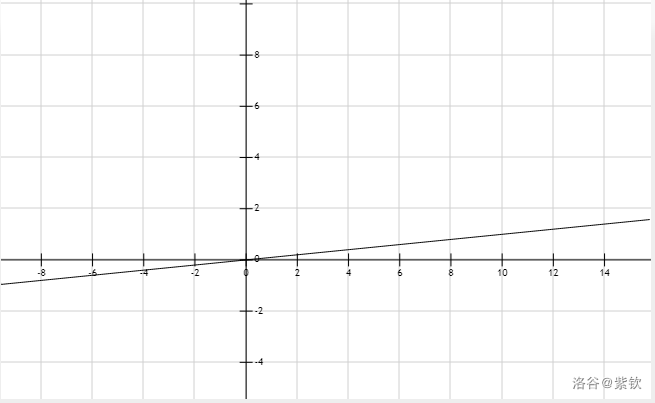： ![](https://cdn.luogu.com.cn/upload/image_hosting/5gxmnl2j.png)

于是这个测试点可以过了。

输出代码

```cpp if(n==8) { // 6 分代码，使用乘法节点。 printf("I\n"); printf("> 1 233\n"); // 造零。 printf("C 2 0.1\n"); // 造0.1。 printf("* 1 3\n"); printf("O 4"); } ``` 满分，$7$ 行： ```cpp if(n==8) { // 7 行。 printf("I\n"); //printf("C 2 2.063437068895560546727281172620131871456591449883392499836032692765902842847409911780353006\n"); printf("> 1 178\n"); printf("C 2 2.0634370688955605467272811726201\n"); // 计算器答案。 printf("S 3\n"); //printf("C 4 -0.887298334620741688517926539978239961083292170529159082658757376611348309193697903351928738\n"); printf("C 4 -0.887298334620741688517926539978236773937633025540819832675154107295416657242528255923059519\n"); printf("< 5 178\n"); printf("O 6"); } ``` # $\text{task9}

要求

输入：a_1,\cdots,a_{16} 。

输入限制：|a_1|,\cdots,|a_{16}|\leqslant10^9 ，小数部分不超过 9 位。

输出：输出 16 个实数，表示 a_1,\cdots,a_{16} 从小到大排序后的结果。

满分行数：3000 。

解决方法

计算节点太单一了，所以有些操作很难实现。

很多高效的排序方法都不能用了，只能使用冒泡排序、选择排序这些基本的算法。

一步一步来考虑。

不管是用什么排序，一个绕不开的操作就是交换两个数。

嗯，怎么交换两个数呢？

~~a^=b^=a^=b~~ 。

（异或需要 539 行，可见在这道题里面位运算可并不快）

我们有加法和减法，所以用这个来实现交换。考虑到每个计算节点只能被赋值一次，我们写出如下代码：
```
u=a+b;
p=u-b;
q=u-p;
```
最终 p 即为交换后的 b ，q 即为交换后的 a 。

——为什么不直接 p=a;q=b; 来完成交换呢？

——因为我们需要同时考虑不交换的情况，故我们的交换操做略微修改后应能够兼容不交换的情况。而直接使用赋值来进行交换会使得我们失去在交换中操作空间，也就没有修改的余地了。

现在考虑不交换的情况，首先我们需要把不交换的操作也写成上面那种形式，并且最好有很多地方与上文完全相同，便于我们构造计算网络。思索一番，我们得到：
```
u=a+b;
p=u-a;
q=u-p;
```
两种写法仅在 p=u-? 处有差别。交换则减 b ，不交换则减 a 。

我们钦定，若 a>b ，则交换；否则不交换。

于是，我们把交换和不交换两种写法合到一起，得到这样的代码：
```
u=a+b;
p=u-min(a,b);
q=u-p;
```
现在问题在于如何计算 \min(a,b) 。
什么样的操作能返回自变量本身呢？记不记得我在上文讲 $\text{task4}$ 时曾说过： > **我们实际上得到的是一个从 $S(x)$ 得到 $x$ 的办法，这个办法很重要。** 就在 $\text{task4}$ 中，我们构造了若干以零为分界点的分段函数。其中一个分段函数（就是 $\text{task4}$ 的答案）为： $-(S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+3}+t+x=\begin{cases}x\ \ \ ,x\geqslant0\\-x,x<0\end{cases}$ ，往回退几步，有这样一个分段函数： $(S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+2}-t=\begin{cases}0,x\geqslant0\\x,x<0\end{cases}$ ，其中 $t=S({\large\frac{x+\varepsilon}{2^q}})\times2^p=\begin{cases}2^p,x\geqslant0\\0\ \ ,x<0\end{cases}$ ，此时的参数为 $q=41,k=178,p=179$ ，**注意此处 $p$ 取值并非 $\text{task4}$ 中最后 $p$ 的取值 $180$ ，而且 $S({\large\frac x{2^{k}}}+t)-{\large\frac12}$ 后面乘的并非 $2^{k+3}$ 。** 而容易发现， $\min(x,0)=\begin{cases}0,x\geqslant0\\x,x<0\end{cases}$ ，所以我们有了一个可以和 $0$ 取 $\min$ 的函数，即 $\min(x,0)=(S({\large\frac x{2^{k}}}+t)-{\large\frac12})\times2^{k+2}-t$ 。将 ```p=u-min(a,b)``` 改写为 ```p=(u-b)-min(a-b,b-b)``` ，即 ```p=a-min(a-b,0)``` 的形式。这个形式就可以用上面得到的 $\min(x,0)$ 来解决了。于是交换的操作完成了，还顺便解决了比大小操作。
解决了交换和比较大小的操作后，我们只需要再选择一种排序方式就能完成任务了。

冒泡排序当然可以（而且还很优美），在这里我试着写了一下 \text{Bitonic Sort} （双调排序）。

双调排序是一个非常适合于 \text{GPU} 编程的排序算法，只需要比较器就可以完成全部的排序工作。

不过它只能对 2 的幂次个数据进行排序，好在此测试点恰好有 16 个数据。

关于双调排序，此处就不赘述了；

我会尽快在我的博客双调排序中具体介绍它（该博客现在处于待填坑隐藏状态，什么时候它不再是隐藏文章了，就说明我填坑完毕了。能力有限，实在抱歉 \cdots\cdots）。

双调排序体现在代码中的 for 循环中，不会双调排序的话，这几个 for 看起来会很费解。。。

输出代码

满分，1392 行：

if(n==9) { // 1392 行。 
    const int N=16; // 数据总数。 
    int pos[17],row=0,a,b; // 16个数据当前的位置，当前输出行数。两个临时节点。 
    for(int i=1;i<=N;++i) printf("I\n"),pos[i]=i,++row;
    for(int i=1,i2=2;i2<=N;++i,i2<<=1) {
        for(int j=1,j2=i2-1;j2>=1;++j,j2-=2) {
            for(int k=j;k<=N;k+=i2) {   // 每次交换 17 行。 
                a=k;b=k+j2;
                ++row;  printf("+ %d %d\n",pos[a],pos[b]);              // u=a+b;
                ++row;  printf("- %d\n",pos[b]);                        // -b;
                ++row;  printf("+ %d %d\n",pos[a],row-1);               // x=a+-b;
                ++row;  printf("C %d 0.0000000001\n",row-1);            // x+eps;
                ++row;  printf("< %d 41\n",row-1);                      // (x+eps)<<41;
                ++row;  printf("S %d\n",row-1);                         // S((x+eps)<<41);
                ++row;  printf("< %d 179\n",row-1);                     // t=S((x+eps)<<41)<<179;
                ++row;  printf("> %d 178\n",row-5);                     // x>>178;
                ++row;  printf("+ %d %d\n",row-1,row-2);                // (x>>178)+t;
                ++row;  printf("S %d\n",row-1);                         // S((x>>178)+t);
                ++row;  printf("C %d -0.5\n",row-1);                    // S(...)-0.5;
                ++row;  printf("< %d 180\n",row-1);                     // (S(...)-0.5)<<180;
                ++row;  printf("- %d\n",row-1);                         // -(S(...)-0.5)<<180;
                ++row;  printf("+ %d %d\n",row-7,row-1);                // -min=t-(S(...)-0.5)<<180;
                ++row;  printf("+ %d %d\n",pos[a],row-1);   pos[b]=row; // p=a-min; b'=p;
                ++row;  printf("- %d\n",row-1);                         // -p;
                ++row;  printf("+ %d %d\n",row-16,row-1);   pos[a]=row; // q=u+-p;  a'=q;
            }
        }
        for(int j=(i2>>2);j>=1;j>>=1) {
            for(int k=1;k<=j;++k) {
                for(int l=k;l<=N;l+=(j<<1)) {
                    a=l;b=l+j;
                    ++row;  printf("+ %d %d\n",pos[a],pos[b]);              // u=a+b;
                    ++row;  printf("- %d\n",pos[b]);                        // -b;
                    ++row;  printf("+ %d %d\n",pos[a],row-1);               // x=a+-b;
                    ++row;  printf("C %d 0.0000000001\n",row-1);            // x+eps;
                    ++row;  printf("< %d 41\n",row-1);                      // (x+eps)<<41;
                    ++row;  printf("S %d\n",row-1);                         // S((x+eps)<<41);
                    ++row;  printf("< %d 179\n",row-1);                     // t=S((x+eps)<<41)<<179;
                    ++row;  printf("> %d 178\n",row-5);                     // x>>178;
                    ++row;  printf("+ %d %d\n",row-1,row-2);                // (x>>178)+t;
                    ++row;  printf("S %d\n",row-1);                         // S((x>>178)+t);
                    ++row;  printf("C %d -0.5\n",row-1);                    // S(...)-0.5;
                    ++row;  printf("< %d 180\n",row-1);                     // (S(...)-0.5)<<180;
                    ++row;  printf("- %d\n",row-1);                         // -(S(...)-0.5)<<180;
                    ++row;  printf("+ %d %d\n",row-7,row-1);                // -min=t-(S(...)-0.5)<<180;
                    ++row;  printf("+ %d %d\n",pos[a],row-1);   pos[b]=row; // p=a-min; b'=p;
                    ++row;  printf("- %d\n",row-1);                         // -p;
                    ++row;  printf("+ %d %d\n",row-16,row-1);   pos[a]=row; // q=u+-p;  a'=q;
                }
            }
        }
    }
    for(int i=1;i<=N;++i) printf("O %d\n",pos[i]);
}

\text{task10}

要求

输入：a,b,m 。

输入限制：0\leqslant a,b<2^{32} ， 1\leqslant m<2^{32} ， a,b,m 均为整数。

输出：a\times b 除以 m 的余数。

满分行数：2000 行。

解决方法

首先，这个式子没有化简的余地。

使用 a\times b\mod m=((a\mod m)\times(b\mod m))\mod m 更不行，虽然每次取余所需的计算节点个数少了，但总的取余次数多了。

看来不管怎么搞，我们都避不开乘法操作。

那就先来讲讲怎么实现乘法。

一个比较容易想到的做法就是使用快速乘，将 b 拆分为二进制，将 a 按 b 不同二进制位上的 0 或 1 相应地做位移后再加起来。

举个栗子，b=5=2^2+2^0 ，则 a\times b=a\times2^2+a\times2^0 。

二进制拆分参见 \text{task6} ，将 a 对应做位移再相加参见 \text{task5} ，有前面的铺垫，这个点的乘法应该怎么计算还是蛮容易想到的。
一个不太容易想到的做法是泰勒展开。

先普及一下泰勒公式：

如果函数 f(x) 在 x=x_0 的某个邻域内有 n 阶导数，且在 x=x_0 处有 n+1 阶导数，则对该邻域内的任意一点 x 处，有
$f^{(n)}(x_0)$ 为 $f(x)$ 在 $x_0$ 处的 $n$ 阶导数。 $o((x-x_0)^{n})$ 表示一个函数，它的表达式我们写不出来，我们只知道它是 $(x-x_0)^n$ 的高阶无穷小。什么意思呢？就是当 $x-x_0$ 无限接近于 $0$ 时，此时的 $(x-x_0)^n$ 是非常非常小的一个数，非常接近于 $0$ ，而 $o((x-x_0)^n)$ 是个比 $(x-x_0)^n$ 还要小很多的数，更接近于 $0$ ——尽管我们并不知道 $o((x-x_0)^n)$ 的具体表达式是什么。 > 不要和我较真说 $o((x-x_0)^n)$ 就等于 $f(x)-(f(x_0)+f'(x_0)(x-x_0)+{\large\frac{f''(x_0)}{2!}}(x-x_0)^2+\cdots+{\large\frac{f^{(n)}(x_0)}{n!}}(x-x_0)^n)$ ， > > 这样写出来的 $o((x-x_0)^n)$ 没有实际意义，并不能清楚地表达 $o((x-x_0)^n)$ 的性质。上面那个**等式**就是 $f(x)$ 的 $n$ 阶泰勒公式，我们一般也将之称为“泰勒展开”。

为什么想到要使用泰勒公式？

核心思想还是想办法利用 S(x) 函数构造乘法。在我们只能做加加减减的情况下，怎么才能快速构造出 a\times b 这样的二次的表达式呢？

这就想到泰勒公式了，因为泰勒公式能将一个函数强行拆成若干多项式以及一个表达式未知但却很小的 o((x-x_0)^n) 的和，所以能够搞出次数为二次的项。有了二次的项，我们的加加减减就能更方便地构造 a\times b 了（之所以认为加加减减不方便，是因为常数次的加加减减不会提高变量的次数，譬如 a 乘任意一个（与 a 无关的）常数都不会变成 a^2）。

那么该怎么用泰勒公式呢？

先将 S(x) 用泰勒公式展开两阶看看。

根据求导的法则，我们得：
$S''(x)={\large\frac{e^{-x}(e^{-x}-1)}{(1+e^{-x})^3}}$ ，则 $S(x)$ 在某点 $x_0$ 处的 $2$ 阶泰勒公式为： $S(x)=S(x_0)+S'(x_0)(x-x_0)+{\large\frac{S''(x_0)}{2!}}(x-x_0)^2+o((x-x_0)^2)$ ，即 $S(x)={\large\frac{1}{1+e^{-x_0}}}+{\large\frac{e^{-x_0}}{(1+e^{-x_0})^2}}(x-x_0)+{\large\frac{e^{-x_0}(e^{-x_0}-1)}{2(1+e^{-x_0})^3}}(x-x_0)^2+o((x-x_0)^2)$ ，换元，用 $x+x_0$ 代替 $x$，得 $S(x+x_0)={\large\frac{1}{1+e^{-x_0}}}+{\large\frac{e^{-x_0}}{(1+e^{-x_0})^2}}x+{\large\frac{e^{-x_0}(e^{-x_0}-1)}{2(1+e^{-x_0})^3}}x^2+o(x^2)$ ，我们取一个比较好的 $x_0$ ，使得上式变得优美一些。比如说取 $x_0=-\ln3$ ，那么上式变成：$S(x-\ln3)={\large\frac{1}{4}}+{\large\frac{3}{16}}x+{\large\frac{3}{64}}x^2+o(x^2)$ ， > ——为什么选 $-\ln3$ ？ > > > 首先可以看到，分母全部变成 $2$ 的倍数了，方便我们用位移来计算除法。 > > > > 当然 $-\ln7$ 什么的也可以，但是写起代码来会麻烦一些。因为 $3=1+2$ 而 $7=1+2+4$ ，会至少多一次位移和一次加法。 > > > > $+\ln3$ 也行，做法基本一致。根据上文所说的关于 $o()$ 函数的含义，我们知道，当 $x$ 非常小、非常接近于 $0$ 时， $o(x^2)$ 也非常接近 $0$ ，且比 $x^2$ 更接近 $0$ 。也就是说，$x$ 趋近于 $0$ 时，$S(x)$ 和 ${\large\frac{1}{4}}+{\large\frac{3}{16}}x+{\large\frac{3}{64}}x^2$ 几乎相等。则我们用 $S(x)$ 减去 ${\large\frac{1}{4}}+{\large\frac{3}{16}}x$ 再乘 ${\large\frac{64}{3}}$ 就可以近似得到 $x^2$ 。按照这个操作，我们可以获得 $a^2,b^2,(a+b)^2$ ，则根据 $a\times b={\large\frac12}((a+b)^2-a^2-b^2)$ 就能构造出 $a\times b$ 了。 *** 好我们还需要解决除以 $3$ 的问题。由于 $S'(x)\leqslant{\large\frac13}$ ，所以我们改为除以 $6$ 再乘 $2$ 。解方程 $S'(\xi)={\large\frac16}$ 得 $\xi=\ln(2+\sqrt3),S(\xi)={\large\frac{3+\sqrt3}{6}}$ ，使用电脑的计算器算得 $\xi=$ ```1.316957896924816708625046347308``` ，再用 ```checker``` 算得 $S(\xi)=$ ```0.788675134594812882254574390250983987152637213723810691381222453707336011601878062966598728``` ，但很遗憾，这样算得的 $\xi$ 和 $S(\xi)$ 精度太低了，在后面的运算过程中小数点后 $9$ 位以内会出现较大误差，所以使用 ```checker``` 的方法宣告 $gg$ 。使用强大的计算器算得 $\xi$ 和 $S(\xi)$ 分别如下： ```1.316957896924816708625046347307968444026981971467516479768472256920460185416443976074219013(4)``` ```0.788675134594812882254574390250978727823800875635063438009301163241988836151466672846857697(7)``` 我们只能用这两个数了。 *** 类似 $\text{task8}$ ，我们用除以 $2^{k}$ 来造极小量， > **这里不能直接用 $k=178$ ，也不能随便设个差不多的数。就因为这一个参数没有设置准确，我调参调了一天，一直 $WA$ 到自闭才找到问题所在。** > > **实测这里的 $k$ 取值范围极其窄。所以务必认真对待以下分析。** 因为 $S'''(x)={\large\frac{e^{-x}(e^{-2x}-4e^{-x}+1)}{(1+e^{-x})^4}}$ ，所以 $S(x)$ 在 $x_0$ 处的 $3$ 阶泰勒公式为： $S(x)=S(x_0)+S'(x_0)(x-x_0)+{\large\frac{S''(x_0)}{2!}}(x-x_0)^2+{\large\frac{S'''(x_0)}{3!}}(x-x_0)^3+o((x-x_0)^3) 用 $x+x_0$ 替换 $x$ ，上式即为： $S(x+x_0)={\large\frac{1}{1+e^{-x_0}}}+{\large\frac{e^{-x_0}}{(1+e^{-x_0})^2}}x+{\large\frac{e^{-x_0}(e^{-x_0}-1)}{2(1+e^{-x_0})^3}}x^2+{\large\frac{e^{-x_0}(e^{-2x_0}-4e^{-x_0}+1)}{(1+e^{-x_0})^4}}x^3+o(x^3)$ ，取 $x_0=-\ln3$ 得 $S(x)$ 在 $-\ln3$ 处的 $3$ 阶泰勒公式为： $S(x-\ln3)={\large\frac{1}{4}}+{\large\frac{3}{16}}x+{\large\frac{3}{64}}x^2-{\large\frac{1}{256}}x^3+o(x^3)$ ，其中 $\lim\limits_{x\to0}o(x^3)=0$ ，甚至 $\lim\limits_{x\to0}{\large\frac{o(x^3)}{x^3}}=0$ 。（第二个式子是 $o(x^3)$ 的定义，在此不详述。第二个式子真正能说明 $o(x^3)$ 比 $x^3$ 还小得多，因为 $o(x^3)$ 除以了一个非常小的数 $x^3$ 之后，极限仍然是 $0$ ）取 $x=$ 微小量 ${\large\frac{a}{2^k}}$ ，可取足够大的 $k$ 使 $x$ 非常接近 $0$ 。现在来求 $k$ 的取值范围：欲使 $S(x-\ln3)={\large\frac{1}{4}}+{\large\frac{3}{16}}x+{\large\frac{3}{64}}x^2$ 近似相等，需要有 $|-{\large\frac{1}{256}}x^3+o(x^3)|<5\times10^{-91}$ 。因为 $o(x^3)$ 真的很小，我们将之忽略，所以只需 ${\large\frac{1}{256}}x^3<5\times10^{-91}$ ，即 ${\large\frac{1}{256}}({\large\frac{a}{2^k}})^3<5\times10^{-91}$ ， $a<2^{32}$ ，故只需 ${\large\frac{1}{256}}({\large\frac{2^{32}}{2^k}})^3<5\times10^{-91}$ ，整理得 $k>{\large\frac{89}3}+30\log_210\approx129.325$ ，所以 $k>130$ 。另一方面，${\large\frac{3}{64}}({\large\frac{a}{2^k}})^2$ 的精度不能丢失，故要求 ${\large\frac{3}{64}}({\large\frac{a}{2^k}})^2>10^{-90}$ ，取 $a=1$ ，只需 ${\large\frac{3}{2^{2k+6}}}>10^{-90}$ ，整理得 $k<45\log_210+{\large\frac12}\log_23-3\approx147.279$ ，所以 $k\leqslant147$ 。然而实测 $k$ 的取值范围为 $[124,131]$ ，个人猜测可能有几点原因： 1. 上述分析有 $\text{bug}$ ，比如即便 ${\large\frac{1}{256}}({\large\frac{2^{32}}{2^k}})^3<5\times10^{-91}$ 成立，第 $91$ 位仍可能产生不该有的进位。再如保证了 ${\large\frac{3}{64}}({\large\frac{a}{2^k}})^2>10^{-90}$ ，也不能保证其小数点后最后一位精度不会丢失。 2. $\ln3,\xi$ 和 $S(\xi)$ 本身只能保留 $90$ 位，在乘 $2$ 的幂次时造成误差。 3. $S(x)$ 函数含超越数 $e$ ，本身很容易产生误差。最终我取了 $k=130$ 。 *** 可以得出：${\large\frac16}x=(S({\large\frac{x}{2^{130}}}+\xi)-S(\xi))\times2^{130}$ ，于是 ${\large\frac{64}3}x=(S({\large\frac{x}{2^{130}}}+\xi)-S(\xi))\times2^{137}$ 。而 ${\large\frac3{16}}x={\large\frac1{16}}x+{\large\frac18}x$ ，两次位移和一次加法可解决。这样，我们就可以计算出 $x^2$ 了。这是 $y=(S({\large\frac{x}{2^{130}}}+\xi)-S(\xi))\times2^{130}$ 的图像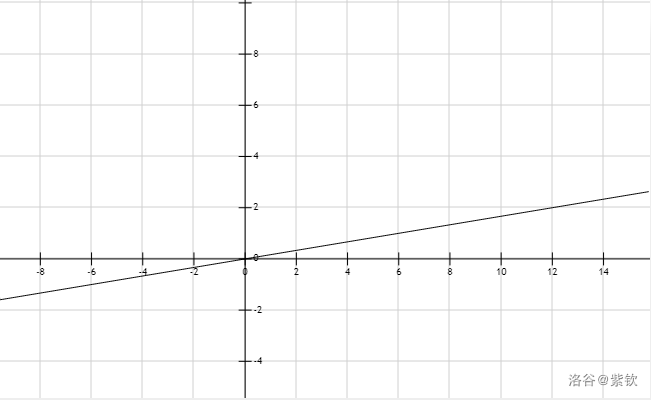： ![](https://cdn.luogu.com.cn/upload/image_hosting/37o4bi1k.png) *** ### 梳理一下思路：令 $t_1=S({\large\frac{a}{2^{130}}}-\ln3)-{\large\frac14}-({\large\frac1{16}}{\large\frac{a}{2^{130}}}+{\large\frac18}{\large\frac{a}{2^{130}}})$ ，则 $({\large\frac{a}{2^{130}}})^2={\large\frac{64}3}t_1=(S(t_1+\xi)-S(\xi))\times2^7$ ； > 这里大家可能会有个疑惑：为什么 $t_1$ 没有除以 $2^{130}$ 就直接放到 $S(x)$ 函数里计算了呢？ > > 其实 $t_1={\large\frac{3}{64}}({\large\frac{a}{2^{130}}})^2+o(({\large\frac{a}{2^{130}}})^2)\approx{\large\frac{3}{64}}({\large\frac{a}{2^{130}}})^2$ ， > > 可见 $t_1$ 仍然是微小量。所以不需要再除以 $2^{130}$ 了。 $({\large\frac{b}{2^{130}}})^2,({\large\frac{a}{2^{130}}}+{\large\frac{b}{2^{130}}})^2$ 同理。最后再乘上 $2^{260}$ 就能还原回 $a^2,b^2,(a+b)^2$ 了。为了减少计算节点，我们将 $S(t_1+\xi),S(t_2+\xi),S(t_3+\xi)$ 都计算出来后，先按照 $((a+b)^2-a^2-b^2)$ 做差，即 $S(t_3+\xi)-S(t_1+\xi)-S(t_2+\xi)$ ，再加上 $S(\xi)$ ，最后乘上 $2^{266}$ ，就可以得到 $a\times b$ 啦。再加一些优化，计算节点数还可以变得更少。具体做法就留给读者自己思索咯。可是 $\ln3$ 怎么算？这个我真的不知道该如何利用 ```checker``` 来计算了。。。使用强大的计算器算得： $\ln3=$ ```1.098612288668109691395245236922525704647490557822749451734694333637494293218608966873615754(8)```

至此，我们用比快速乘更少的节点（ 35 个）计算出了 a\times b 。

下面讲如何完成取余操作。

取余操作，可以等效为若干次减法操作。

设 a\times b=p\times m+r ，其中 0\leqslant r<m ，

那么，一个显然的做法就是：

我们枚举这个 p ，如果 a\times b 比当前枚举到的 p\times m 大，则继续往大枚举；否则往小枚举。

这样搞的计算节点数当然会多到爆炸啦。

由于 a\times b<2^{64} ，

所以考虑直接将 p 二进制拆分，即 p=p_0\times2^0+p_1\times2^1+\cdots+p_{63}\times2^{63} ，其中 p_i\in\{0,1\},i\in[0,63] 。

然后从高位到低位枚举 p_i ，当前 ab 比 m\times2^{i} 大，则将 m\times2^i 从 ab 中减去。直到 i=0 ，操作完成后即得 r ，即余数。

为了减少计算节点数，我们先将 ab 取反，变成 -ab ，然后每次加上 m\times2^i ，最后把得到的 -r 取反即得 r 。这样我们在计算 ab 时的方式也要相应的调整，变为 {\large\frac12}(a^2+b^2-(a+b)^2) ，同时调整一些细节即可。

至于如何调整，留给读者自己思考完成吧。

那么具体如何比较大小呢？

考虑对于 M=m\times2^i ，如何正确执行 \begin{cases}-ab+M\ ,-ab+M\leqslant0\\-ab\ \ \ \ \ \ \ \ \ \ ,-ab+M>0\end{cases} 呢？

首先我们可以得到一个函数 p=\begin{cases}0,\ -ab+M<0\\1,\ -ab+M>0\end{cases} ，

这样的话， p=0 就代表要让 -ab 加上 M ，p=1 代表不加上 M 。

由于 -ab+M 一定是整数，且 -ab+M=0 时也应该执行加上 M 的操作，所以我们将 -ab 提前减去 0.1 ，从而使得我们的 p 能够处理 -ab+M=0 的情形。

则此时 p=\begin{cases}0,\ -ab+M\leqslant0\\1,\ -ab+M>0\end{cases} ，

我们想要的是 \begin{cases}-ab+M\ ,-ab+M\leqslant0\\-ab\ \ \ \ \ \ \ \ \ \ ,-ab+M>0\end{cases} ，利用 p 可以将之改写为 -ab+(1-p)\times M ，

考虑到 1-p 只有 0,1 两种取值，所以我们只需要构造 (1-p)M=\begin{cases}M\ ,p=0\\0\ \ \ ,p=1\end{cases} ，

这个形式的函数我们在 \text{task4} 中讲过，以下再简述一番。

将 M 拆为 (S({\large\frac{M}{2^{178}}})-0.5)\times2^{180} ，考虑在这个过程中加入 p 的影响。

构造 t=p\times2^{179}=\begin{cases}0\ \ \ \ \ ,p=0\\2^{179}\ ,p=1\end{cases} ，作为 p 的影响。

将 t 加入上述过程中，即 (S({\large\frac{M}{2^{178}}}+t)-0.5)\times2^{180}=\begin{cases}M\ \ \ ,p=0\\2^{179}\ ,p=1\end{cases} ，

减去 t ，消除多余影响，得 (S({\large\frac{M}{2^{178}}}+t)-0.5)\times2^{180}-t=\begin{cases}M\ ,p=0\\0\ \ \ ,p=1\end{cases} ，

于是做完了。

共 807 行，比官方题解的 819 行略少。

开心。

输出代码

满分，807 行：

if(n==10) { // 807 行。
    const int W=130;
    char ln3[]={"1.098612288668109691395245236922525704647490557822749451734694333637494293218608966873615755"};

    //  1.316957896924816708625046347307968444026981971467516479768472256920460185416443976074219013
    // -0.25
    // =1.066957896924816708625046347307968444026981971467516479768472256920460185416443976074219013
    char xi []={"1.066957896924816708625046347307968444026981971467516479768472256920460185416443976074219013"};

    //  0.78867513459481288225457439025097872782380087563506343800930116324198883615146667 2846857698
    // +0.00000000000000000000000000000000000000000000000000000000000000000000000000000000 0843375836  // 0.1>>266;
    // =0.78867513459481288225457439025097872782380087563506343800930116324198883615146667 3690233534
    char Sxi[]={"0.788675134594812882254574390250978727823800875635063438009301163241988836151466673690233534"};
    printf("I\n");                      
    printf("I\n");
    printf("I\n");
    printf("> 1 %d\n",W);
    printf("> 2 %d\n",W);               // 5。 
    printf("+ 4 5\n");
    printf("C 4 -%s\n",ln3);            
    printf("C 5 -%s\n",ln3);            
    printf("C 6 -%s\n",ln3);            
    printf("S 7\n");                    // 10。 
    printf("S 8\n");
    printf("S 9\n");
    printf("> 4 4\n");                  
    printf("> 4 3\n");
    printf("> 5 4\n");                  // 15。 
    printf("> 5 3\n");
    printf("+ 13 14\n");
    printf("+ 15 16\n");
    printf("- 17\n");
    printf("- 18\n");                   // 20。 
    printf("+ 19 20\n");
    printf("+ 10 19\n");
    printf("+ 11 20\n");
    printf("+ 12 21\n");
    printf("C 22 %s\n",xi);             // 25。 
    printf("C 23 %s\n",xi);
    printf("C 24 %s\n",xi);
    printf("S 25\n");
    printf("S 26\n");
    printf("S 27\n");                   // 30
    printf("+ 28 29\n");
    printf("- 30\n");
    printf("+ 31 32\n");
    printf("C 33 -%s\n",Sxi);
    printf("< 34 %d\n",W*2+6+41);       // 35。 // 提前左移 41 位，加上本来应该左移的 266 位。 
    for(int i=36,j=63;j>=0;--j,i+=12) {
        printf("< 3 %d\n",41+j);        // M=m<<i;
        printf("+ %d %d\n",i,i-1);      // -ab+M;
        printf("S %d\n",i+1);           // p=S((-ab+M)<<41);
        printf("< %d 179\n",i+2);       // t=p<<179;
        printf("> %d 178\n",i);         // M>>178;
        printf("+ %d %d\n",i+4,i+3);
        printf("S %d\n",i+5);
        printf("C %d -0.5\n",i+6);
        printf("< %d %d\n",i+7,180);
        printf("- %d\n",i+3);           // -t;
        printf("+ %d %d\n",i+9,i+8);
        printf("+ %d %d\n",i+10,i-1);   // -ab+M or -ab+0;
    }
    printf("> 803 41\n");
    printf("C 804 0.100000000064\n");   // 因为 0.1>>266 时产生了一些精度误差，所以在这个地方往回补一补精度。 
    printf("- 805\n");
    printf("O 806");
}

结语

本篇题解作为旷野大计算的题解，思路清晰，解法自然，逻辑严谨，你可以利用这篇题解，为自己的解题之旅进行热身。

苯蒟蒻相信，这篇优美的题解，可以给拼搏于获奖的逐梦之路上的你，提供一个有力的援助。

~~不好意思走错片场了。~~
整体代码就不往上放了，这里是评测记录。
利用好 S(x) 函数。该函数是本题的灵魂。~~这话说着容易做起来难。~~ 极限是本题的经脉，使灵魂有了承载。二者结合，我认为是本题最重要的思想。

利用连续函数构造分段函数，是二者结合的具体体现。
注意计算节点的优化，有些可以特殊处理的就拿出来单独处理。单独处理往往能减少计算节点个数。
我尽可能减少计算节点，并成功把 \text{task7,task10} 的计算节点数压到了官方题解以下。

~~可把我牛逼坏了。~~
关于 \text{task4,task8} 中将函数视作直线的误差分析，同样可使用 \text{task10} 中泰勒展开的方式来做。
定义结构体、使用函数来输出、重载运算符，从而将自己的代码让程序自动按执行顺序翻译成题目所给的计算节点的形式。这样的操作更有利于调试和编程，也方便理解，而且可移植性非常强。若按照我的写法，修改代码的时候，很多表示计算节点编号的参数都需要重新计算。输出调试的时候麻烦更甚！

虽然我这种最底层编写方式能带给我些许减少计算节点的可能，但就题论题，我减少掉的那几个计算节点其实无关紧要。

所以最好不要参照我的这种写法，参照 ljc1301 \text{dalao} 的题解或者 da32s1da \text{dalao} 所给出的官方题解都可以。

官方题解的代码写法真的让在下甘拜下风，比我的不知高明了多少，太方便了！
双调排序积极填坑中。
本题真的是在造一台计算机。也可视作使用一种较低级语言进行编程。
本题的 checker 可以留下来，我觉得蛮有用的。
本题解 \text{posted on \color{red}01\color{black}:\color{red}23\color{black}:\color{red}4\color{balck}8} ！

很遗憾秒数没有卡准。
终于做完了这道题，总体来说还是很有成就感的。

为了写这篇题解，放弃期末复习，我也是很有胆魄了（捂脸）。

我已经尽可能减少错别字了，期望能带给读者最好的阅读体验。

这篇题解基本上真实地还原了我的思考历程，~~当然省略了我看题解的过程~~，可以算是事无巨细，为的是能够带给前来查阅题解的人一些思路，也为了将尽可能严谨的分析贡献出来，更为了将我对这道题更本质的思考展现给大家，希望能给大家一些题目以外的启迪。

诚挚感谢您的阅读，希望我的题解能帮到您。祝 AC 愉快。

解题报告P1737 [NOI2016]旷野大计算

解法：构造答案

\text{task1}

要求

解决方法

输出代码

\text{task2}

要求

解决方法

输出代码

\text{task3}

要求

解决方法

回顾题目

怎么利用 S 函数呢？

那么如何取极限？

输出代码

\text{task4}

要求

解决方法

要求

解决方法

输出代码

\text{task6}

要求

解决方法

输出代码

要求

解决方法

输出代码

要求

解决方法

输出代码

要求

解决方法

输出代码

\text{task10}

要求

解决方法

为什么想到要使用泰勒公式？

那么该怎么用泰勒公式呢？

输出代码

结语