题解:P14171 【MX-X23-T1】丢手绢
hydk2012
·
·
题解
丢呀丢呀丢手绢,轻轻放在小朋友后面,大家不要告诉她,快点快点抓住她,快点快点抓住她。
话说这题怎么出奇的水。
思路
一目了然,就是存储每个小朋友(NpY)被放手绢的次数,进行排序再输出即可。
这里每个小朋友扔手绢后的位置我们可以进行举例:
我们把小朋友的位置抽象为一个环。就像这样:
那么我们就可以来看一看丢手绢的小朋友与被放手绢的小朋友下标的关系。
例如:编号为 1 的小朋友放在了顺时针 2 个位置上:
可以发现手绢在 3 号小朋友的位置上。
再比如,还是编号为 1 的小朋友,他又放在了逆时针 3 个位置上:
现在又在 2 号小朋友的位置上。
不管 a_i 是正的负的,我们都要用丢手绢的小朋友的位置下标加上 a_i,再取模 n。
这样我们可以大概推出这个关系式:
int pos=(i+k-1)%n+1;
但有的同学可能会推出这个式子:
`int pos=(i+k)%n;`
这显然是不对的,你手动模拟一下 $1$ 号小朋友放在了顺时针 $3$ 个位置上:
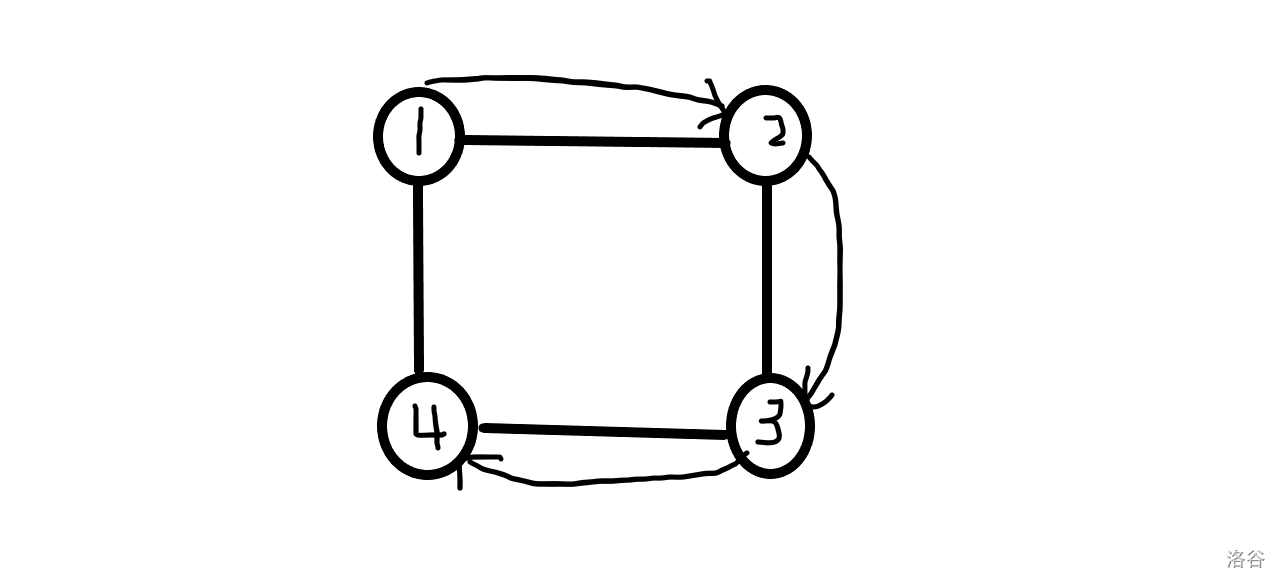
显然是 $4$ 号小朋友的位置上。但这个式子推出来却是 $0$ 号小朋友,自然是错了。
还有一个点,我们推出来被放手绢的小朋友的下标可能会小于 $1$,这个时候就要额外特判,下标要加一个 $n$,不然就会 RE。
## Code:
```cpp
#include<bits/stdc++.h>
using namespace std;
struct node
{
int id; // 记录小朋友位置下标,排完序输出时要用。
int cnt=0; // 记录小朋友的人气值,即被放了几次手绢。
}a[1000005];
int n;
bool cmp(node a,node b)
{
if(a.cnt!=b.cnt) return a.cnt>b.cnt; // 按次数由大到小排序。
return a.id<b.id; // 次数相同按编号由小到大排序。
}
signed main()
{
cin>>n; // 输入。
for(int i=1;i<=n;i++)
{
int k;
a[i].id=i; // 记录小朋友位置下标。
cin>>k; // 输入当前小朋友丢的距离,即a_i。
int pos=(i+k-1)%n+1; // 通过距离计算是哪个小朋友被放了手绢。
if(pos<1) pos+=n; // 下标小于1,要加上n。
a[pos].cnt++; // 人气值++。
}
sort(a+1,a+n+1,cmp); // 排序。
int k=a[1].cnt; // 记录最高人气值。
for(int i=1;i<=n;i++)
{
if(a[i].cnt==k) cout<<a[i].id<<' '; // 这个小朋友的人气值是最高的之一,输出。
}
return 0;
}
```
感谢阅读!!!