P9870 [NOIP2023] 双序列拓展
Nightingale_OI
·
·
题解
简单转化
实际上,题目的 q 是为了减少输入而存在的,每次求解复杂度为 O(n+m)。
由于 $f_1=x_1$,$g_1=y_1$,可以确定是哪种情况,不妨假设 $f_i>g_i$。
## 思路
记 $A_{[l,r]}$ 表示 $A$ 数组从第 $l$ 到第 $r$ 个元素依次排列构成的数组。
$l>r$ 时 $l,l-1,\dots,r+1,r$ 这么数,当然 $1\leq l,r\leq |A|$。
---
原问题相当于给定一个二分图,上点 $i$ 和下点 $j$ 可以连边当且仅当 $x_i>y_j$。
求是否可以每个点至少连一条边且所有边不交(重边视为相交)。
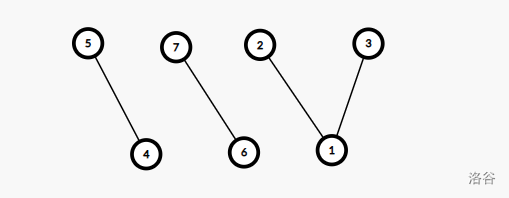
上图是一组合法解的转换方式。
发现如果存在边 $(i,j)$ 和边 $(i+1,j+1)$,一定可以存在边 $(i,j+1)$ 或 $(i+1,j)$。
这是好证的,$x_i>y_j,x_{i+1}>y_{j+1}$,假设不存在边 $(i,j+1)$ 即 $x_i\leq y_{j+1}$,则 $x_{i+1}>y_{j+1}\geq x_i>y_j$ 即存在边 $(i+1,j)$。
由此,我们需要为这个二分图连 $n+m-1$ 条不交的边,每个点至少连了一条边。
---
由于我们钦定 $f_i>g_i$,所以特殊性质为 $x_n$ 是唯一最大值,$y_m$ 是唯一最小值。
若 $Y$ 中存在元素不小于 $x_n$,显然无解,同理 $X$ 中存在元素不大于 $y_m$ 也无解。
显然最后一定存在一条边 $(n,m)$,考虑其它一定存在的边。
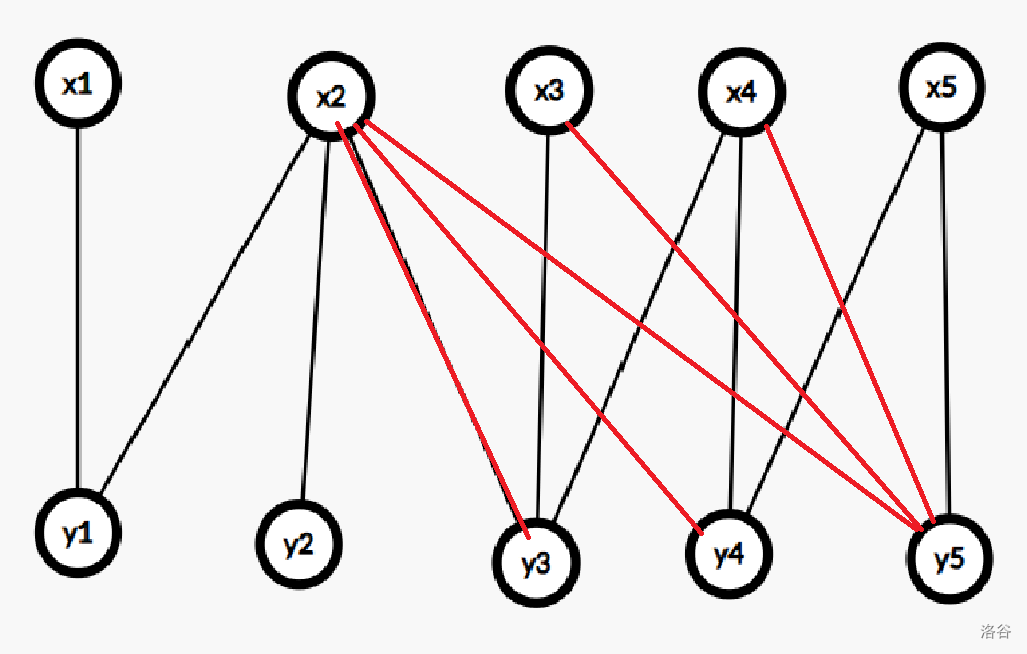
若存在 $x_p$ 使得 $x_p>\max Y$,则一定可以存在边 $(p,m)$。
考虑一种合法方案,找到关于 $p$ 的任意边 $(p,q)$,根据大小关系 $(p,q\sim m)$ 和 $(p\sim n,m)$ 都可以连。
则原问题 $\{X,Y\}$ 和子问题 $\{X_{[1,p]},Y\}$ 等价。
同理,若有 $y_q<\min X$,则一定可以存在边 $(n,q)$ 且其右必定有解。
则原文题 $\{X,Y\}$ 和子问题 $\{X,Y_{[1,q]}\}$ 等价。
递归边界是 $n=1$ 时必定存在 $(1,1\sim m)$ 的边,问题有解,$m=1$ 同理。
考虑如果 $x_p$ 和 $y_q$ 都不存在的情况(当然可以取 $x_{p=n}$ 和 $y_{q=m}$,但是对问题规模变小没用,忽略)。
我们设 $x_a=\min X_{[1,n-1]},y_b=\max Y_{[1,m-1]}$,则必须存在边 $(a,m)$ 和 $(n,b)$,但是这两条边相交,无解。
不难证明递归构造出的连边方式满足 $n+m-1$ 条不交的边,每个点至少连了一条边。
当 $r$ 增加时,最小的满足 $x_p>\max Y_{[1,r]}$ 的 $p$ 单调不降,拿个数组维护,$y_q$ 同理,复杂度 ${\rm O}(n+m)$。
每次问题规模的 $n+m$ 至少变小 $1$,复杂度 ${\rm O}(n+m)$。
总复杂度 ${\rm O}(n+m)$,值得一提的是我们并没有用到最值唯一的性质,也没有用到是最值的性质,只要满足 $x_n>\max Y$ 和 $y_m<\min X$ 就行,所以可以递归。
---
发现只要从 $X$ 的任意最大值 $x_p$ 和 $Y$ 的任意最小值 $y_q$ 处劈开。
原问题 $\{X,Y\}$ 有解等价于 $\{X_{[1,p]},Y_{[1,q]}\}$ 有解且 $\{X_{[n,p]},Y_{[m,q]}\}$ 有解,这两个子问题都满足特殊性质。
## 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define f(i,j,k) for(int i=j;i<=k;++i)
#define g(i,j,k) for(int i=j;i>=k;--i)
int n,m,s,l;
const int N=505050,inf=1e9+7;
inline int read(){
int x=0;
char ch=getchar();
for(;!('0'<=ch&&ch<='9');ch=getchar());
for(;'0'<=ch&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);
return x;
}
int a[N],b[N],c[N],d[N],pa[N],pb[N],oa[N],ob[N];
inline int clac(int *a,int*b,int n,int m){
if(a[1]<=b[1])return 0;
a[n+1]=inf;b[m+1]=-inf;
int w=inf,p=1;
f(i,1,n){
for(w=min(w,a[i]);b[p]>=w;)++p;
pa[i]=p;
}
w=-inf;p=1;
f(i,1,m){
for(w=max(w,b[i]);a[p]<=w;)++p;
pb[i]=p;
}
while(n>1&&m>1){
if(pa[n]<m){m=pa[n];continue;}
if(pb[m]<n){n=pb[m];continue;}
return 0;
}
return 1;
}
inline int doing(int*a,int*b,int n,int m){
a[0]=-inf;b[0]=inf;
int pa=0,pb=0;
f(i,1,n)if(a[i]>a[pa])pa=i;
f(i,1,m)if(b[i]<b[pb])pb=i;
f(i,1,n)if(a[i]<=b[pb])return 0;
f(i,1,m)if(b[i]>=a[pa])return 0;
int na=0,nb=0;
f(i,1,pa)c[++na]=a[i];
f(i,1,pb)d[++nb]=b[i];
if(!clac(c,d,na,nb))return 0;
na=nb=0;
g(i,n,pa)c[++na]=a[i];
g(i,m,pb)d[++nb]=b[i];
if(!clac(c,d,na,nb))return 0;
return 1;
}
signed main(){
int c,q,ka,kb;
c=read();n=read();m=read();q=read();
f(i,1,n)oa[i]=read();
f(i,1,m)ob[i]=read();
f(_,0,q){
f(i,1,n)a[i]=oa[i];
f(i,1,m)b[i]=ob[i];
if(_){
ka=read();kb=read();
f(e,1,ka)c=read(),a[c]=read();
f(e,1,kb)c=read(),b[c]=read();
}
if(a[1]>b[1])putchar(doing(a,b,n,m)^48);
else putchar(doing(b,a,m,n)^48);
}
return 0;
}
```