最大流ISAP算法

· · 题解

看见没有 ISAP 的题解，蒟蒻刚学 ISAP 就贡献一个吧。

步入正题

1.ISAP 算法是什么？

是一种计算网络流的高效最短增广路算法，它其实是优化版的最短增广路算法，最短增广路算法即 EK 算法。

2.Dinic 算法和 ISAP 算法的区别？

Dinic 算法每次 DFS 后，会从源点 s 到汇点 t 进行一次 BFS 来维护层次图。但 ISAP 算法从始至终只进行一次从汇点 t 到源点 s 的 BFS，但 DFS 的时候要同时维护结点的深度。

3.ISAP 算法具体有哪些步骤？

1.首先，从汇点 t 到源点 s 进行一次 BFS。

2.然后，每次沿着深度连续的结点进行增广，然后更新路径上的结点深度。

3.如果某个深度不存在或者源点 s 的深度大于等于结点个数 n 时结束，否则转步骤 2（不是转步骤 1）

ISAP 的神奇之处在于它不用再进行 BFS 就能维护层次图。

首先是初始化历程，这里使用链式前向星进行存图。

#define inf 1000000000000000
#define V 20010
#define E 500010
typedef long long int ll;
struct edge {
public:
    int to, next;
    ll capa;
};
int cnt = 0, head[V]; int n, m; vector<edge>node(E);
inline void add(int fir, int nxt, ll w) {
    node[cnt].to = nxt;
    node[cnt].capa = w;
    node[cnt].next = head[fir];
    head[fir] = cnt; ++cnt;
}
int s, t, dep[V], gap[V], cur[V]; queue<int>que; ll sum = 0;
inline void initing() {
    memset(dep, -1, (n + 1) * sizeof(int));
    memcpy(cur, head, (n + 1) * sizeof(int));
}

其中有三个新数组：分别是 dep, gap 和 cur。

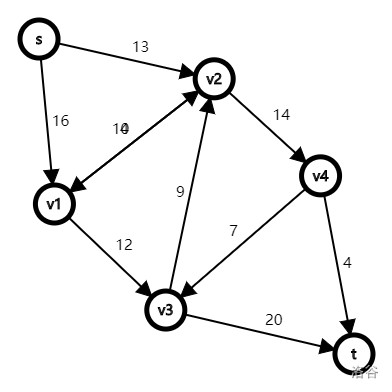
在图 $G=(V,E)$ 中， $dep$ 可以对应于一个新函数 。 $$ \operatorname{dep}(u),u \in V $$ 它代表这个结点的**深度**。你先不要纠结深度是什么，下面会讲。 同样， $gap$ 也可以对应一个新函数。 $$ \operatorname{gap}(d),d \in \operatorname{deep(u)},u \in V $$ 它代表**这个深度对应的结点数**。 那它们有什么用呢？ 先放图。 ![](https://cdn.luogu.com.cn/upload/image_hosting/6306ndod.png) 因为工具的限制，反向弧以及结点 $v1$ 和 $v2$ 之间的重边无法正常展示。 ISAP 会先用 BFS 造层次图。注意是从汇点 $t$ 开始 BFS ，不是从源点 $s$ 开始的。 下面是 BFS 后图的状态。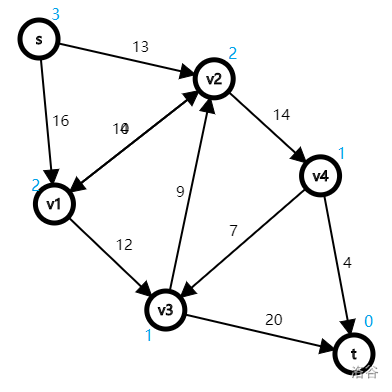 ![](https://cdn.luogu.com.cn/upload/image_hosting/e3tznebx.png) 具体过程如下： 1.将汇点 $t$ 入队。 2.**遍历队首结点每个出边**，将边对应的结点入队，**入队的结点深度为队首结点深度 +$1$** 3.将队首结点出队，**如果队列不为空，转步骤 $2$，否则直接结束** 注意，这里有一个坑点： ```cpp if (dep[ito] == -1) ``` BFS 的时候一定只通过深度判定是否遍历过，不能判定边权大小，因为初始反向边是没有边权的，而我们因为是从汇点 $t$ 开始 BFS 的，所以要通过反向边才能到达源点 $s$。 代码如下： ```cpp void bfs() { int fro, i, ito; que.push(t); deep[t] = 0; ++gap[deep[t]]; while (!que.empty()) { fro = que.front(); que.pop(); for (i = head[fro]; i != -1; i = node[i].next) { ito = node[i].to; if (deep[ito] == -1) {//不要特判边权为 0 deep[ito] = deep[fro] + 1; que.push(ito); ++gap[deep[ito]];//别忘了给 gap 加 1 } } } } ``` 有了这个深度有什么用呢？**能让我们找到的增广路一定是最短增广路。** 怎么走呢？ 首先给 DFS 两个参数：“当前结点 $u$” 和 “从 $s$ 到 $u$ 增广路径上最小边权 $flow$”。再加上一个变量：“当前结点已经增广出去的流量 $used$ ”。 记住下面几个原则： 1.从源点 $s$ 开始 DFS。 2.只沿着**深度连续**的增广路径增广，只通过边权不为 $0$ 的边增广。 3.当 $used$ 等于 $flow$ 时及时停止。 4.当增广后 $used$ 小于 $flow$ 时将结点 $u$ 的深度 +$1$。 先看看代码感受一下。 ```cpp ll dfs(int u, ll flow) { if (u == t || flow == 0)return flow; ll used = 0; for (int i = cur[u]; i != -1; i = node[i].next;) { cur[u] = i; if (dep[u] == dep[node[i].to] + 1 && node[i].capa > 0) { ll wei = dfs(node[i].to, min(flow - used, node[i].capa)); if (wei) { node[i].capa -= wei; node[i ^ 1].capa += wei; used += wei; } } if (used == flow)return used; } if (used > flow)used = flow; if (used < flow) { --gap[dep[u]]; if (!gap[dep[u]])dep[s] = n + 1; ++gap[++dep[u]]; } //这里的 if 语句才是与 Dinic 算法真正的不同之处 return used; } ``` 你大概听说过一个与 ISAP 几乎一致的算法：“Dinic 算法”。 Dinic 算法与 ISAP 算法有一点不一样： Dinic 在 DFS 后直接暴力 BFS 维护层次图，但是 ISAP 却在 DFS 的时候也在维护层次图。这一点不同导致 ISAP 算法的运行速度往往比 Dinic 算法快上数倍。 ISAP 算法是这样维护层次图的：如果从上一个结点传过来的流量大于从这个结点增广出去的流量，那么将这个结点的深度 +$1$。 就是这么简洁。 你可能还想问：“为什么 ‘当增广后 $used$ 小于 $flow$ 时将结点 $u$ 的深度 +$1$’ 呢？” 请看： ```cpp if (used < flow) { --gap[dep[u]]; if (!gap[dep[u]])dep[s] = n + 1; ++gap[++dep[u]]; } ``` ISAP 的思想在这短短的几行代码里表现得淋漓尽致。 为什么这是对的？ 假设有一个结点 $u \in V$ 是当前 DFS 考虑的结点，并且我们知道汇点 $t$ 的深度是不变的，因为我们遇到了汇点 $t$ 就 ```return```，而源点 $s$ 的深度是每轮必变的，因为初始源点 $s$ 的 $flow$ 是 $\infty$。 这可以推导出一个很重要的结论：“**当前 DFS 找到的增广路径长度相等且都等于 $\operatorname{dep}(s)$**”。 这意味着如果有一个结点 $u \in V$， 从 $u$ 增广出去的流量小于增广路径上最小边权的容量，也就意味着**经过 $u$ 的所有长度等于 $\operatorname{dep}(s)$ 的增广路都已经被增广过了**，而且通过这个结论我们也可以证明，所有长度小于 $\operatorname{dep}(s)$ 的增广路都已经被增广完了。 **这时候将结点 $u$ 的深度提高，相当于通过结点 $u$ 的增广路径长度变长了，也就能增广其他比原本的增广路更长的增广路了。** #### 结束条件， gap 优化以及当前弧优化 ```cpp while (dep[s] < n) { sum += dfs(s, inf); memcpy(cur, head, (n + 1) * sizeof(int)); } ``` 这是运行 ISAP 的核心代码之一。 可以看到结束条件是 ```dep[s]<n``` 。 为什么呢？因为增广路最长只有 $n$，```dep[s]``` 等于 $n$ 时增广路肯定都找完了。 那 gap 优化又是优化到那里了呢？ ```cpp if (used < flow) { --gap[dep[u]]; if (!gap[dep[u]])dep[s] = n + 1; ++gap[++dep[u]]; } ``` 无比的合理，当一个深度对应的结点数目为 $0$ 的时候，那么就会形成断层，也就找不到增广路了，找不到增广路就说明已经是最大流了。这里利用 ```dep[s]=n+1``` 还能使程序少一个特判。 程序还使用了一个优化：“当前弧优化”。 当前弧优化的核心在这里： ```cpp for (int i = cur[u]; i != -1; i=node[i].next) { cur[u] = i; ... } ``` 这里的作用是：当我们再次遍历到这个点时，前面的边肯定已经被增广完了，就没必要再走了，在这里进行一次剪枝，速度也极大提升。 #### ISAP 的正确性： 在图 $G=(V,E)$ 中，很显然源点 $s$ 的深度在每次 DFS 后都会提高，并且每次 DFS 都找的是最短增广路，如果一直没出现断层，定义函数 $\operatorname{dep}(U),U \in V$ 为结点 $U$ 的深度。 最多会跑 $V-\operatorname{dep}(s)$ 次增广路，可以证明，当 $\operatorname{dep}(s) ≥ V$ 时必定出现断层，也就不存在增广路径，因此 ISAP 算法找出的一定是最大流。 #### 时间复杂度分析： 在图 $G=(V,E)$ 中，BFS 是 $\Theta(V+E)$ 的，几乎不影响总时间复杂度。显然，每次 DFS 后，源点 $s$ 到汇点 $t$ 的距离都会增加 $1$，最多进行 $V-\operatorname{dep}(s)$ 次 DFS，直观上看，$\operatorname{dep}(s)$ 比 $V$ 的阶小，因此共进行 $O(V)$ 次 DFS，每次构造出一个新的层次图，图上最多有 $O(E)$ 个增广路，寻找每个增广路的时间最多是 $O(V)$ 的，所以 ISAP 算法的时间复杂度上限为 $O(V^2E)$。 证毕。 ACcode ```cpp #include <bits/stdc++.h> using namespace std; #define inf 1000000000000000 #define V 50010 #define E 1000010 typedef long long int ll; struct edge { public: int to, next; ll capa; }; int cnt = 0, head[V]; int n, m; vector<edge>node(E); inline void add(int fir, int nxt, ll w) { node[cnt].to = nxt; node[cnt].capa = w; node[cnt].next = head[fir]; head[fir] = cnt; ++cnt; } int s, t, deep[V], gap[V], cur[V]; queue<int>que; ll sum = 0; inline void initing() { memset(deep, -1, V * sizeof(int)); memcpy(cur, head, (n+1)*sizeof(int)); } inline void bfs() { int fro, ito; que.push(t); deep[t] = 0; ++gap[deep[t]]; while (!que.empty()) { fro = que.front(); que.pop(); for (register int i = head[fro]; i != -1; i = node[i].next) { ito = node[i].to; if (deep[ito] == -1) { deep[ito] = deep[fro] + 1; que.push(ito); ++gap[deep[ito]]; } } } } ll dfs(int u, ll flow) { if (u == t || flow == 0)return flow; ll used = 0,wei=0; for (int i = cur[u]; i != -1; i = node[i].next) { cur[u] = i; if (deep[u] == deep[node[i].to] + 1 && node[i].capa > 0) { wei = dfs(node[i].to, min(flow - used, node[i].capa)); if (wei) { node[i].capa -= wei; node[i ^ 1].capa += wei; used += wei; } } if (used == flow)return used; } if (used < flow) { --gap[deep[u]]; if (!gap[deep[u]])deep[s] = n + 1; ++gap[++deep[u]]; } return used; } ll ISAP() { initing(); bfs(); while (deep[s] < n) { sum += dfs(s, inf); memcpy(cur, head, (n+1) * sizeof(int)); } return sum; } int main() { ios::sync_with_stdio(0); memset(head, -1, V*sizeof(int)); cin >> n >> m >> s >> t; int f, n; ll w; for (register int i = 0; i < m; i++) { cin >> f >> n >> w; add(f, n, w); add(n, f, 0); } cout << ISAP(); return 0; } ```