题解 CF1149C 【Tree Generator™】
command_block
·
·
题解
题意 : 给出一棵以括号序列描述的树。
资瓷交换两个括号(不一定相邻,保证仍为一棵树),求直径。
------------
同学 : 欸这个括号序列挺有趣的,你学不学啊。
我 : 这个题搞个欧拉序也行吧,再不济直接动态链分治。改天再学吧 (咕
直到我遇见了这题……题目中直接蕴含该知识点。
括号序可以视作有进有出的`dfs`序,有如下结论:
- 选取 $u,v$ 之间的括号,全部**匹配**对消完毕之后,剩余形如 `))))(((`。
剩余括号个数即为 $dis(u,v)$ ,可以给括号加权。
证明 : 考虑到达 $a$ 点时 $b$ 的两个括号可能的状态。
- ① 均填完
$b$ 不是 $a$ 的祖先或子孙。
- ② 均未填
$b$ 不是 $a$ 的祖先。
- ③ 只填写了左边
$b$ 是 $a$ 的祖先。
$u,v$ 之间,能够匹配的括号们,对于 $u$ 是情况②,对于 $v$ 是情况①,均不在路径上。
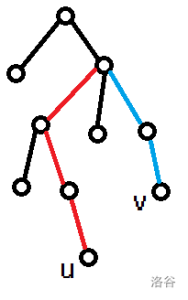
对于余下的右括号,对于 $u$ 是情况③,对于 $v$ 是情况 ①,对应 “既是 $u$ 的祖先,又不是 $v$ 的祖先”的路径,即为蓝色部分。
对于余下的左括号,对于 $u$ 是情况②,对于 $v$ 是情况 ③,对应 “既是 $v$ 的祖先,又不是 $u$ 的祖先”的路径,即为红色部分。
红蓝两种颜色恰好拼成 $u,v$ 两点间的路径。
那么,我们只需要维护任意区间内未匹配括号的最大数量即可。
给 $"("$ 赋权 $+1$ , 给 $")"$ 赋权 $-1$ 。
一段括号序列对消完毕之后,假设分界线前面的和为 $s1$ (负数),分界线后面的和为 $s2$ ,则剩余括号个数为 $s2-s1$。
若我们选择的不是实际的分界线,答案一定更劣(依赖于权值非负),所以不必特殊考虑。
现在就是要维护 : 相邻的两段区间和的差的最大值。资瓷单点修改。
使用线段树维护。
每个区间要记录区间和 $s$ ,最小后缀 $r0$ ,最大后缀 $r1$ ,最小前缀 $l0$ ,最大前缀 $l1$,
左侧完整(贡献为负),经过分界线,右侧贴右端点的最大值 $rm$。
右侧完整,经过分界线,左侧(贡献为负)贴左端点的最大值 $lm$。
左右侧均贴端点的最大值 $lrm$。
区间内部的答案 $m$。
> 觉得费脑子可以直接`DDP`,然后化简矩阵,不过估计也挺麻烦。
转移具体细节请见代码。
```cpp
#include<algorithm>
#include<cstdio>
#include<vector>
#define MaxN 200500
using namespace std;
struct Node
{int s,r0,l1,rm,lm,lrm,m;}
a[MaxN<<2];
inline void up(int u)
{
int l=u<<1,r=u<<1|1;
a[u].s=a[l].s+a[r].s;
a[u].l1=max(a[l].l1,a[l].s+a[r].l1);
a[u].r0=min(a[l].r0+a[r].s,a[r].r0);
a[u].lm=max(a[l].lm,max(a[l].lrm+a[r].l1,a[r].lm-a[l].s));
a[u].rm=max(a[r].rm,max(a[r].lrm-a[l].r0,a[l].rm+a[r].s));
a[u].lrm=max(a[l].lrm+a[r].s,a[r].lrm-a[l].s);
a[u].m=max(max(a[l].m,a[r].m),max(a[l].rm+a[r].l1,a[r].lm-a[l].r0));
}
char str[MaxN];
int n,m;
void build(int l=1,int r=n,int u=1)
{
if (l==r){
int x=(str[l]=='(' ? 1 : -1);
a[u].l1=max(x,0);a[u].r0=min(a[u].s=x,0);
a[u].rm=a[u].lm=a[u].lrm=a[u].m=(x<0 ? -x : x);
return ;
}int mid=(l+r)>>1;
build(l,mid,u<<1);
build(mid+1,r,u<<1|1);
up(u);
}
int to;
void chg(int l=1,int r=n,int u=1)
{
if (l==r){
int x=(str[l]=='(' ? 1 : -1);
a[u].l1=max(x,0);a[u].r0=min(a[u].s=x,0);
a[u].rm=a[u].lm=a[u].lrm=a[u].m=(x<0 ? -x : x);
return ;
}int mid=(l+r)>>1;
if (to<=mid)chg(l,mid,u<<1);
else chg(mid+1,r,u<<1|1);
up(u);
}
int main()
{
scanf("%d%d%s",&n,&m,str+1);
n=n*2-2;
build();printf("%d\n",a[1].m);
for (int i=1,x,y;i<=m;i++){
scanf("%d%d",&x,&y);
swap(str[x],str[y]);
to=x;chg();
to=y;chg();
printf("%d\n",a[1].m);
}return 0;
}
```