P4572 题解
liangbowen
·
·
题解
前言
题目传送门!
更好的阅读体验?
双倍经验:P3554(数据坑一点)。简要题意可以看 P3554。
思路:二分答案 + 树形 DP。
思路
答案显然具有单调性,所以考虑二分答案。
容易想到贪心,但实际上并不可行。这是同机房巨佬的 [hack](https://www.luogu.com.cn/discuss/503923)。于是考虑 DP。
---
首先两人都很聪明,所以 B 会一直从根往下走;A 会一直在 B 下面的层染色。
最麻烦的是,在对一个子树染色时,可能会出现染不够的情况。但这并不意味着 $k$ 不成立,因为 $i$ 的祖先可能会有剩余的没有染色。
听起来非常难懂,举个例子,$k = 3$。
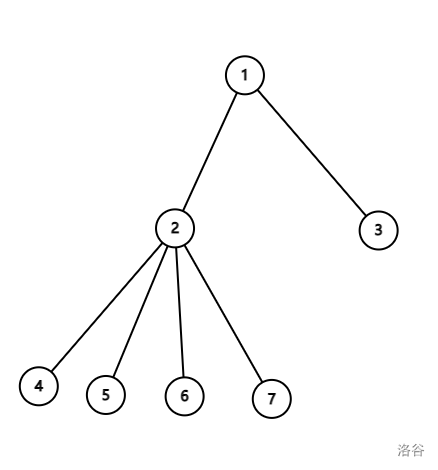
如果只看以 $2$ 为根的子树,显然无法染完。
但是如果看以 $1$ 为根的整棵树,发现:染完 $2,3$ 号点后还能再染一次,这样可以帮 $2$ 为根的子树染一下。于是 $k = 3$ 就成立了。
我们就可以用这个性质实现 DP。
---
设 $dp_i$ 表示以 $i$ 为根的子树,需要 $dp_i$ 次祖先的帮助。
那么就有转移方程(为了美观,分了两行):
$$\texttt{sum} = \sum\limits_{\text{v : son of u}} dp_v + 1$$
$$dp_u = \max\{0, \texttt{sum} - k\}$$
$\texttt{sum}$ 即为子树需要的帮助次数。每次加 $(dp_v + 1)$,是因为还要染 $v$,所以加了一。
那么 $k$ 能成立,当且仅当 $dp_1 = 0$。
这题就愉快地做完啦!
## 完整代码
```cpp
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 3e5 + 5;
struct Edge {int now, nxt;} e[N << 1];
int head[N], cur;
void add(int u, int v)
{
e[++cur].now = v;
e[cur].nxt = head[u];
head[u] = cur;
}
int k, dp[N];
void dfs(int u, int fa) //按照转移方程来就好了
{
int sum = 0;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].now;
if (v != fa) dfs(v, u), sum += dp[v] + 1;
}
dp[u] = max(0, sum - k);
}
bool chk(int x)
{
k = x, dfs(1, -114514);
return !dp[1]; //等同于 return dp[1] == 0
}
int FIND(int l, int r) //二分答案
{
while (l < r)
{
int mid = (l + r) >> 1;
if (chk(mid)) r = mid;
else l = mid + 1;
}
return r;
}
int main()
{
ios::sync_with_stdio(false);
int n;
cin >> n;
for (int i = 1; i < n; i++)
{
int u, v;
cin >> u >> v;
add(u, v), add(v, u);
}
cout << FIND(0, n); //注意 l=0,否则 n=1 会叉掉
return 0;
}
```
希望能帮助到大家!