浅析 AC 自动机
FTAC
·
2025-09-30 16:39:25
·
算法·理论
哈喽大家好,我是 doooge,今天来点大家想看的东西啊。
\Huge \sf 浅析~AC~自动机
前置知识:Trie,不需要 KMP。
1. AC 自动机的构造与匹配
所谓 AC 自动机,是结合了 Trie 和 KMP 思想的自动机,简单来说就是一个 Trie 图,用于解决字符串多模式匹配的问题。
AC 自动机由两个部分构成:原本的 Trie 和若干个失配指针 fail ,下面给一道它的例题。
有一个文本串 T 和 n 个模式串 S_i ,求有几个模式串在文本串中出现过。
如果用暴力匹配,复杂度是 O(n^2) 的,不够优秀。直接讲 AC 自动机的做法。
1.1 建树
构建 AC 自动机的第一步是将所有的模式串加入 Trie,跟普通的 Trie 一样。
例如,有 3 个字符串 ABCD,ABD 和 BD,建完的树是这样的,记 x 的字符为 y 子节点为 t_{x,y} :
值得注意的是,Trie 上除了根的每一个节点都是一个模式串的前缀(这也是字典树的性质)
但是,就算建好了这棵树,我们也不好匹配,因为我们不知道模式串是在文本串的哪个位置出现的,这个时候,就要用到我们的失配指针 fail 了。
1.2 失配指针
闲话:失配指针这个东西是从 KMP 里借鉴过来的,当然本人觉得这个东西比 KMP 里的 next 数组要好理解。
定义 i 属于的字符串为从根节点 Root 所出发到节点 i ,途中经过的字符组成的字符串。
失配指针是用于辅助文本串转移的,记 fail_x 为 x 的 fail 指针。
我的理解是,fail_i 表示的是,fail_i 所属的字符串为 i 所属的字符串最长的后缀。
很抽象,用图来解释吧:
因为节点 5 属于的子串为 ABD,节点 7 属于的子串为 BD 且是图中所有最长的后缀(当然也只有它一个),所以 fail_5=7 。
如果多了一个模式串 D,它们之间的 fail 指针是这样的:
那么,我们如何才能求出 fail 指针呢?我们假设已经知道 fa 的 fail 指针,如何才能求出子节点 fail 的指针呢?
我们知道子节点想要后缀最大,肯定是继承父节点 fail 指针最优,比如说下图:
首先,我们先查找节点 5 的父节点的 fa_5=2 ,因为 2 号节点的 fail 节点 6 有相邻为 D 的子节点,所以 fail_5=t_{6,D}=7 。
但是还有一个特殊情况,这里同样给个例子
首先,我们同样查找节点 3 的父节点的 fa_3=2 ,因为 2 号节点的 fail 节点 6 并没有相邻边为 D 的子节点,所以我们想要答案最优,就得继续跳 fail ,我们跳到 fail_6 ,也就是根节点,虽然这里仍然没有相邻为 D 的边,但是此时的根节点已经跳不动了,所以 fail_3=0 ,也就是根节点。
但是,如果一直暴力跳 fail ,复杂度最坏是 O(n) 的,我们如何才能优化呢?我们可以建若干个虚拟节点,而这个节点指向它的 fail 。
如图,我们在 4 号节点下建一个用 C 边连接的虚拟节点 BC,指向的是 BC 的 fail ,我们要建 ABC 的 fail 时就能直接查询到 BC 这个节点,进而查到 C 这个 fail ,因为原本的 Trie 上没有 BC 这个节点,所以一定能保证后续我们通过虚拟节点查到的 fail 一定时最优的。
下面给了个更加复杂的例子,这里就不作过多解释了。
进一步,我们可以用 BFS 来求,使得求到 x 的 fail 时深度比 x 小的能先求出来。
于是,构建 fail 指针的步骤是这样的:
将根节点的所有子节点入队,根节点的虚拟节点的 fail 都指向根。
每次取出队首的节点 x ,枚举每一个字符 i ,若 t_{x,i} 是空的,建出 x 的所有虚拟节点指向那个节点的 fail ,可以写成:
t_{x,i}=fail_{t_{x,i}}=t_{fail_x,i}
此时 t_{x,i} 的 fail 指针一定不会是空的,因为深度小于 x 的节点的虚拟节点已经求完了。
否则,建出 t_{x.i} 的 fail 指针并将其入队:
fail_{t_{x,i}}=t_{fail_x,i}
重复 2 到 3 操作,直到队列为空停止。
这一段的时间复杂度为 O(n|\sum|) ,其中 |\sum| 表示字符集的大小,跑起来如果 |\sum| 大一点(比如小写字母)就和 O(n\log n) 差不多了。
下面用图解 fail 指针建造过程(模式串只有 A,B,C 三种字符构成):
首先,我们将根节点的子节点 1,5,7 入队(忘画 4 节点见谅):
先取出节点 1 ,构建 1 的虚拟节点和子节点 2 的 fail ,将 2 入队:
再取出节点 5 ,建出虚拟节点和子节点 6 的 fail (这里 6 的 fail 画成虚边了见谅,后面改回来了),将 6 入队:
如法炮制节点 7,2,6,3 ,然后就画成了这么一坨幅图:
1.3 AC 自动机的匹配
AC 自动机的匹配过程如下(文本串为 T ):
初始 pos 节点为根(0 )。
设 k 为 pos ,每次暴力往上面跳 k=fail_k ,过程中打上标记 vis_k=1 ,只要发现 vis_k 之前被标记过了就停止,途中记录经过了哪些节点在 Trie 上是某个模式串的结尾节点。
最后看有哪些模式串所在的节点被经过了就是答案。
下面给出解释:
时间复杂度:$O(n)$。
匹配过程如下(还是之前的那一~~坨~~幅图):
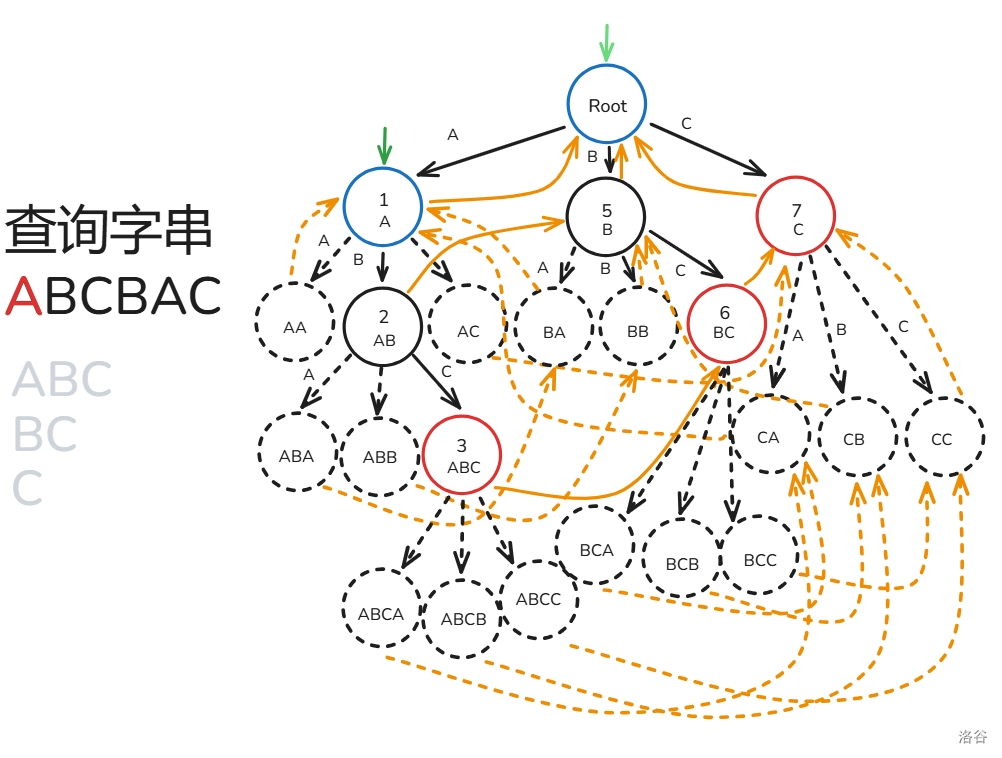
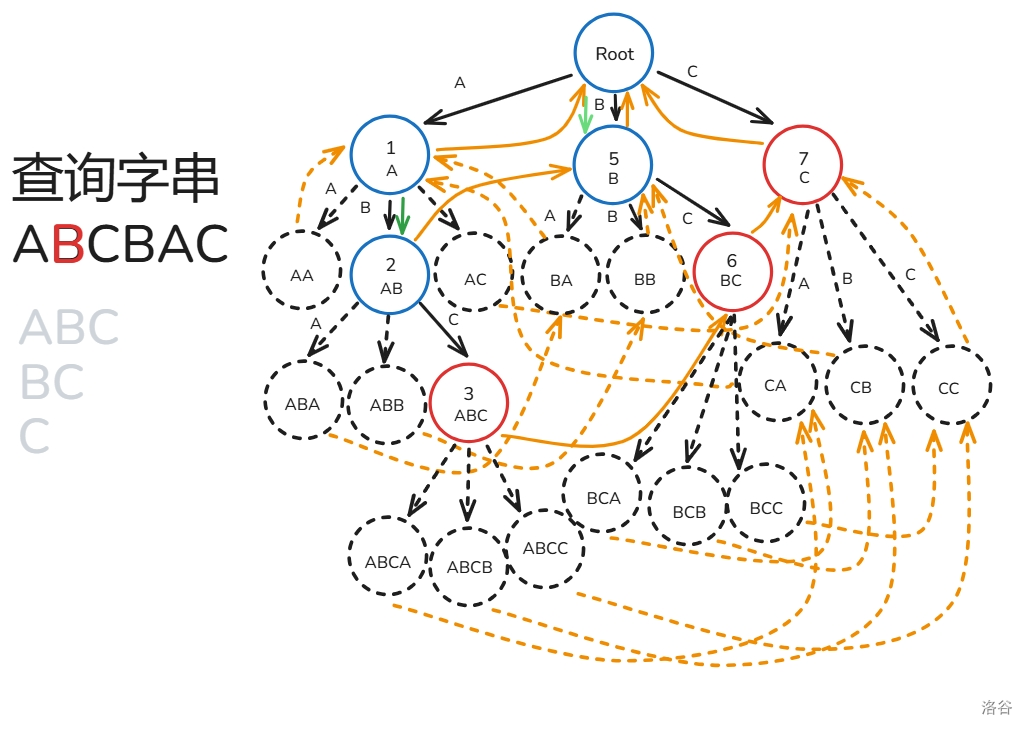
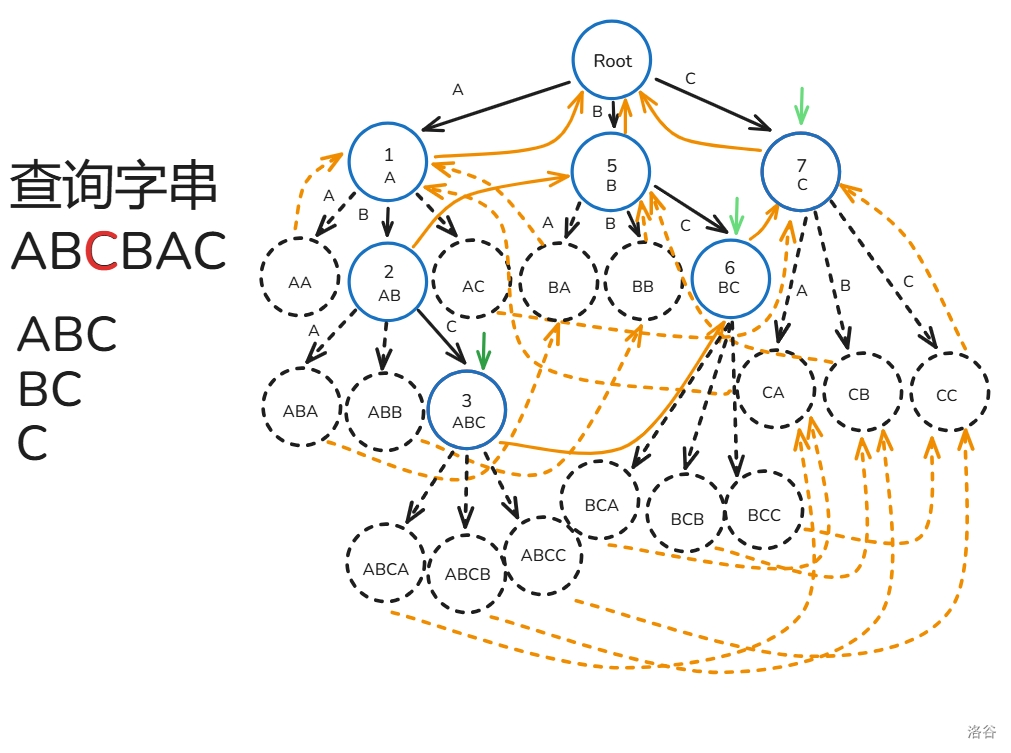
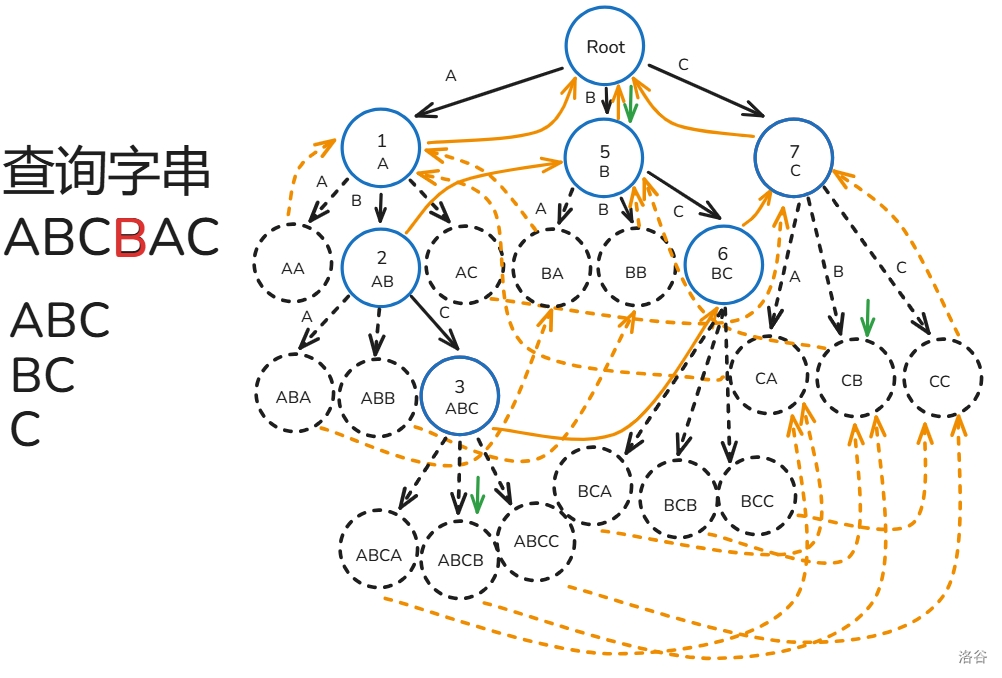
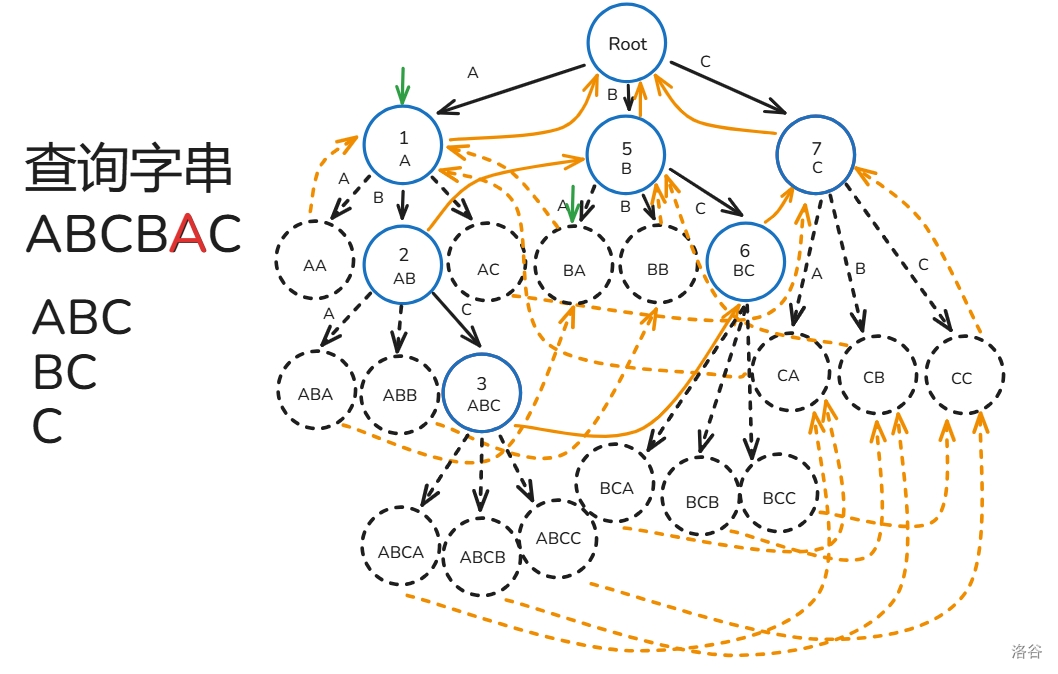
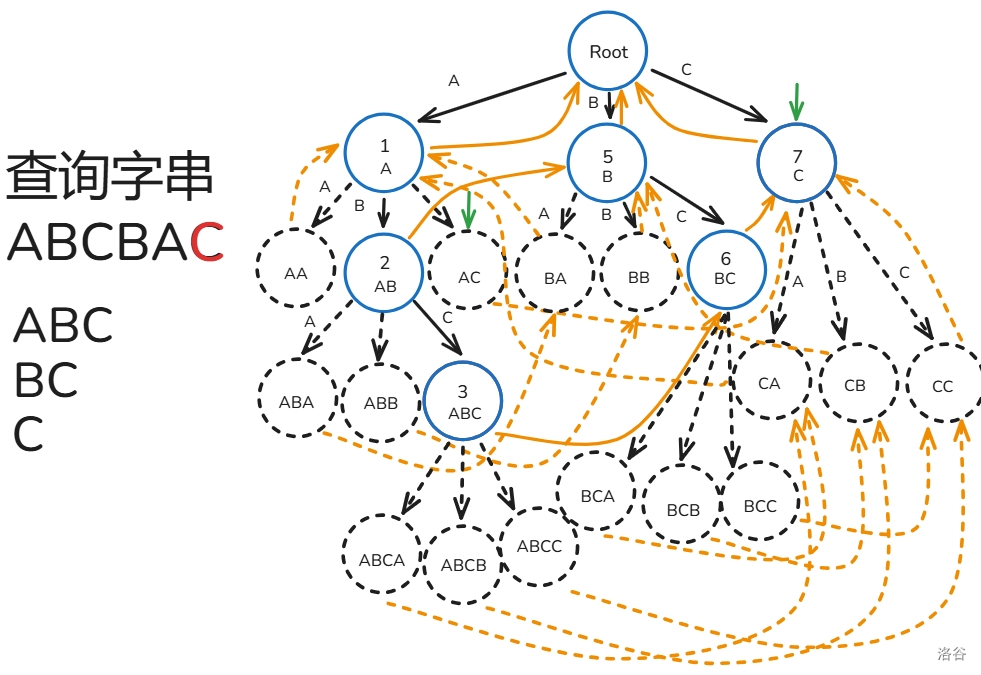
至此,你已经掌握 AC 自动机的大部分了!
# 2. 代码
模板题:[P3808](https://www.luogu.com.cn/problem/P3808)。
```cpp
#include<bits/stdc++.h>
using namespace std;
struct ll{
int flag,fail,son[30];
//flag表示这个节点有几个模式串的尾节点
}t[1000010];
int cnt=1,ans;//根节点从1开始,方便等下fail处理
bool vis[1000010];
void build(string s){//就是普通的Trie插入
int pos=1;
for(int i=0;i<s.size();i++){
if(!t[pos].son[s[i]-'a']){
t[pos].son[s[i]-'a']=++cnt;
}
pos=t[pos].son[s[i]-'a'];
}
t[pos].flag++;
return;
}
void build_fail(){
queue<int>q;
for(int i=0;i<26;i++)t[0].son[i]=1;
t[1].fail=0;
q.push(1);//我习惯这么写,当然可以把根的子节点都丢进去
while(!q.empty()){
int tmp=q.front();
q.pop();
for(int i=0;i<26;i++){
if(!t[tmp].son[i]){//构建虚拟节点
t[tmp].son[i]=t[t[tmp].fail].son[i];
continue;//这时就不用入队了
}
t[t[tmp].son[i]].fail=t[t[tmp].fail].son[i];
q.push(t[tmp].son[i]);//处理子节点
}
}
return;
}
void query(string s){
int pos=1;
for(int i=0;i<s.size();i++){
pos=t[pos].son[s[i]-'a'];
int k=pos;
while(!vis[k]){//跳fail
ans+=t[k].flag,vis[k]=true;
k=t[k].fail;
}
}
return;
}
int main(){
int n;
string s;
cin>>n;
for(int i=1;i<=n;i++){
string x;
cin>>x;
build(x);
}
build_fail();
cin>>s;
query(s);
cout<<ans<<endl;
return 0;
}
```
# 3. 拓扑建图优化
还是放一道例题([P5357](https://www.luogu.com.cn/problem/P5357)):
> 有一个文本串 $T$ 和 $n$ 个模式串 $S_i$,求每个模式串在文本串中出现的次数。
> $(n,|T|\le 10^6,\sum_{i=1}^{n}|S_i|\le 10^6)$,字符串中只包含小写字母。
求出每个模式串的个数可不好搞,因为一个模式串在文本串中出现过多次,只用 $vis$ 数组标记肯定是不正确的,但是暴力跳 $fail$ 的时间实在太长。
我们可以回想一下刚刚的查询是怎么找答案的,我们能否优化这个跳 $fail$ 的过程呢?答案是肯定的,比如说下面这幅图(蓝色表示经过的节点):
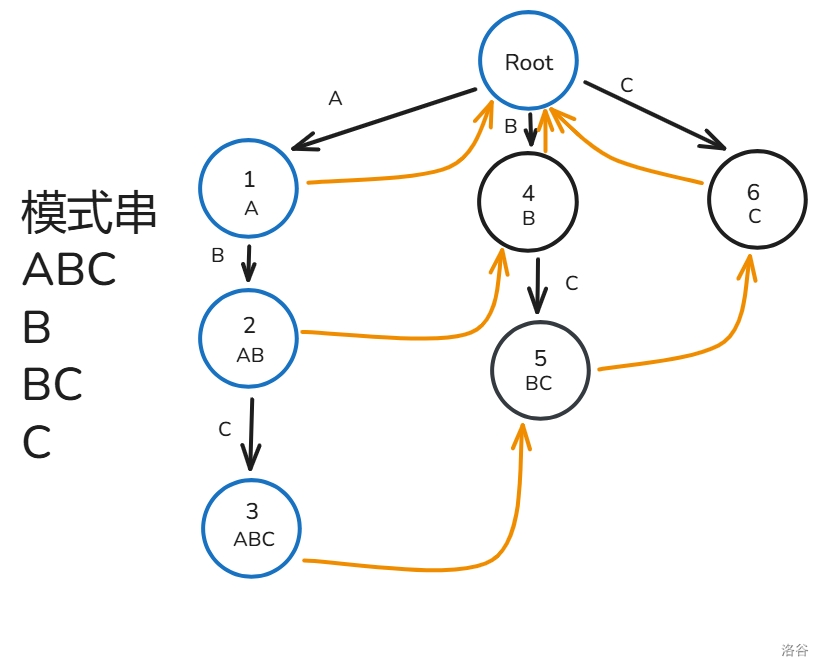
我们发现 $fail$ 指针只会指向深度比自己低的节点,也就是说一直跳 $fail$ 不会遇到一个环,这不就是一张有向无环图吗?
我们把 $fail$ 指针看成边,然后就可以进行拓扑来求到答案,因为我们知道如果能够匹配到 $x$,也一定能够匹配到 $fail_x$。
具体来说,我们预处理出匹配过的路径,使路径上的 $vis_x=1$,然后我将 $x$ 到 $fail_x$ 看作成单向边,将图中入度为 $0$ 的点丢进队列里去,每次找队首 $x$,使 $vis_{fail_x}$ 加上 $vis_x$,其中 $vis$ 表示出现次数,入队和普通的拓扑一样,最后答案就是每个模式串所在的 Trie 上的节点的 $vis_x$ 了。
完整代码如下:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int Root=1;//Root=1
struct ll{//trie
int fail,flag,ans,son[35];//flag表示有几个模式串的结尾在这个节点
}t[200010];
int ans[200010],vis[200010],in[200010],mp[200010];
int cnt=1;//节点数量
void build(string s,int q){//trie内添加s
int pos=Root;
for(int i=0;i<s.size();i++){
if(t[pos].son[s[i]-'a']==0){
t[pos].son[s[i]-'a']=++cnt;
}
pos=t[pos].son[s[i]-'a'];
// cout<<pos<<endl;
}
if(!t[pos].flag)t[pos].flag=q;
mp[q]=t[pos].flag;
return;
}
void build_fail(){//0的子节点指向Root,Root的Fail指针指向0
fill(t[0].son,t[0].son+26,Root);
queue<int>q;
t[Root].fail=0;
q.push(Root);
while(!q.empty()){
int tmp=q.front();
q.pop();
// cout<<tmp<<endl;
for(int i=0;i<26;i++){//父亲转移儿子
int v=t[tmp].son[i];
if(v==0){//没有这个儿子
t[tmp].son[i]=t[t[tmp].fail].son[i];//t[tmp].son[i]更新为t[t[tmp].son[i]].fail
continue;
}
t[v].fail=t[t[tmp].fail].son[i];//t[tmp].fail一定有i这个儿子
in[t[v].fail]++;//x->fail[x]
q.push(v);
}
}
return;
}
void query(string s){//寻找
int pos=Root;
for(int i=0;i<s.size();i++){
pos=t[pos].son[s[i]-'a'];
t[pos].ans++;
}
return;
}
void topo(){
queue<int>q;
for(int i=1;i<=cnt;i++){
if(in[i]==0)q.push(i);
}
while(!q.empty()){
int tmp=q.front();
q.pop();
vis[t[tmp].flag]=t[tmp].ans;
int x=t[tmp].fail;
in[x]--,t[x].ans+=t[tmp].ans;
if(in[x]==0)q.push(x);
}
return;
}
int main(){
ios::sync_with_stdio(0);
int n;
string s;
cin>>n;
for(int i=1;i<=n;i++){
string x;
cin>>x;
build(x,i);
}
build_fail();
// cout<<"input end.\n";
cin>>s;
memset(ans,0,sizeof(ans));
query(s);
topo();
for(int i=1;i<=n;i++){
cout<<vis[mp[i]]<<endl;
}
return 0;
}
```
# 4. AC 自动机上 DP
先给个例题([P3041](https://www.luogu.com.cn/problem/P3041)):
> 有 $n$ 个模式串 $s_i$,构造一个长度为 $k$ 的字符串,使得所有模式串在这个字符串中出现次数之和最大,询问这个最大的值是多少。\
> ($n\le20$,$|s_i|\le15$,$k\le10^3$),字符串只有 `A`,`B`,`C` 这三个字符组成。
直接来想 DP 如何做这道题,我们先想想如何构造状态。
不难想到,我们可以设字符串的长度 $i$,字符为 $j$ 结尾最大的答案为 $dp_{i,j}$。
但是怎么转移呢?因为我们只知道最后一个字符,假设我们枚举的状态 $dp_{i,B}$ 是 `...B`,此时来了一个 `ABA` 的模式串,$dp_{i+1,A}$ 肯定会加上 $dp_{i,B}$ 的贡献,$dp_{i-1,A}$ 的贡献,但是如果有个 `BA` 的模式串,$dp_{i,B}$ 也加上了 $dp_{i-1,A}$ 呢?所以这个状态设计的不对。
我们来考虑在 DP 上套 AC 自动机,首先,长度这个状态肯定是要保留的,我们可以新增加一个维度表示此时在 Trie 上的哪个节点,也就是说,$dp_{i,j}$ 表示的是长度为 $i$,$1$ 到 $i$ 所构成的字符串上以节点 $j$ 结尾。
那么转移也就很简单了:
$$dp_{i+1,t_{j,k}}=dp_{i,j}+cnt_{t_{j,k}}(k\in \{A,B,C\})$$
$cnt_x$ 表示的是多少个模式串是节点 $x$ 属于的子串的后缀,这个可以暴力跳 $fail$ 或者在处理 $fail$ 指针是就将其处理好。
答案在 $dp_{m,i}$ 中取 $\max$ 就行了!
完整代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
struct ll{
int fail,flag,son[20];
}t[310];
int dp[1010][310],cnt=1;
void build(string s){
int pos=1;
for(int i=0;i<s.size();i++){
if(t[pos].son[s[i]-'A']==0){
t[pos].son[s[i]-'A']=++cnt;
}
pos=t[pos].son[s[i]-'A'];
}
t[pos].flag++;
return;
}
void build_fail(){
for(int i=0;i<3;i++){
t[0].son[i]=1;
}
t[1].fail=0;
queue<int>q;
q.push(1);
while(!q.empty()){
int tmp=q.front();
q.pop();
for(int i=0;i<3;i++){
int x=t[tmp].son[i];
if(x==0){
t[tmp].son[i]=t[t[tmp].fail].son[i];
continue;
}
t[x].fail=t[t[tmp].fail].son[i];
q.push(x);
}
t[tmp].flag+=t[t[tmp].fail].flag;
}
return;
}
int main(){
int n,m,ans=0;
cin>>n>>m;
for(int i=1;i<=n;i++){
string s;
cin>>s;
build(s);
}
build_fail();
for(int i=0;i<=m;i++){
for(int j=2;j<=cnt;j++){
dp[i][j]=-1e9;
}
}
for(int i=1;i<=m;i++){
for(int j=1;j<=cnt+1;j++){
for(int k=0;k<3;k++){
dp[i][t[j].son[k]]=max(dp[i][t[j].son[k]],dp[i-1][j]+t[t[j].son[k]].flag);
}
}
}
for(int i=0;i<=cnt;i++){
ans=max(ans,dp[m][i]);
}
cout<<ans<<endl;
return 0;
}
```
总结:AC 自动机上的 DP 一般都会有长度和节点位置这两项状态。
# 5. 例题
## 5.1 P2444 [POI 2000] 病毒
> 有 $n$ 个由 ${0,1}$ 组成的模式串,问能否构造一个长度无限只包含 ${0,1}$ 的字符串不包含任何的模式串,如果能,输出 `TAK`,否则输出 `NIE`
> $1\le n\le 2\times 10^3$,所有模式串的长度不超过 $3\times 10^4$。
首先,构造一个满足条件无限长的字符串,一定可以按一种循环结尾。
比如说这个例子:
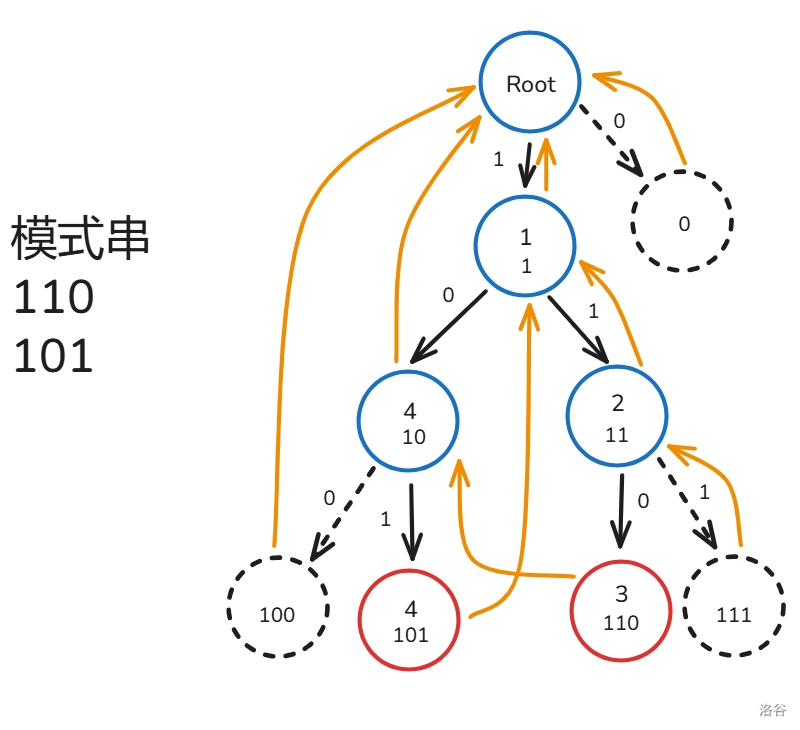
我们想想一个循环的字符串在匹配过程中是什么样子的。例如 `100100..`,我们依次经过的结点是:`Root,1,4,Root,1,4...`,不难发现,这是在绕着一个环来走,当然可以举更多的例子:`111111...`,这个例子与刚刚的有些不同,它经过的结点是 `Root,1,2,2,2...`,最后也是绕着一个环来走。
我们可以得出结论:一个循环的字符串在匹配过程中,指针最后一定会绕着某个环来走,这个证明不难,我在这里就不写了~~其实是我懒~~。
我们想要一个满足条件的字符串,在匹配时就不能经过模式串尾节点或直接 / 间接通过 $fail$ 能到达的模式串尾节点的节点,这个能在处理 $fail$ 指针的时候就搞好,于是这道题的做法也就想出来了:在自动机上找到一个不包含任何一个直接或间接通过 $fail$ 指针到达某个模式串的尾节点的环(当然尾节点自己也不行),这个东西用 DFS 就好了。
完整代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,cnt=1;
bool vis[30010],f[30010];
struct Trie{
int fail,son[5];
bool flag;
}t[30010];
void build(string s){
int pos=1;
for(int i=0;i<s.size();i++){
if(!t[pos].son[s[i]-'0']){
t[pos].son[s[i]-'0']=++cnt;
}
pos=t[pos].son[s[i]-'0'];
}
t[pos].flag=true;
}
void build_fail(){
for(int i:{0,1})t[0].son[i]=1;
t[1].fail=0;
queue<int>q;
q.push(1);
while(!q.empty()){
int tmp=q.front();
q.pop();
for(int i:{0,1}){
if(!t[tmp].son[i]){
t[tmp].son[i]=t[t[tmp].fail].son[i];
continue;
}
t[t[tmp].son[i]].fail=t[t[tmp].fail].son[i];
t[t[tmp].son[i]].flag|=t[t[t[tmp].fail].son[i]].flag;
q.push(t[tmp].son[i]);
}
}
return;
}
void dfs(int x){
if(vis[x]){
cout<<"TAK\n";
exit(0);
}
vis[x]=1;
for(int i:{t[x].son[0],t[x].son[1]}){
if(f[i]||t[i].flag)continue;
dfs(i);
f[i]=1;
}
vis[x]=0;
return;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
string s;
cin>>s;
build(s);
}
build_fail();
dfs(1);
cout<<"NIE\n";
return 0;
}
```
## 5.2 P2414 [NOI2011] 阿狸的打字机
> 阿狸喜欢收藏各种稀奇古怪的东西,最近他淘到一台老式的打字机。打字机上只有 $28$ 个按键,分别印有 $26$ 个小写英文字母和 `B`、`P` 两个字母。经阿狸研究发现,这个打字机是这样工作的:
>
> - 输入小写字母,打字机的一个凹槽中会加入这个字母 (这个字母加在凹槽的最后)。
> - 按一下印有 `B` 的按键,打字机凹槽中最后一个字母会消失。
> - 按一下印有 `P` 的按键,打字机会在纸上打印出凹槽中现有的所有字母并换行,但凹槽中的字母不会消失。
> 我们把纸上打印出来的字符串从 $1$ 开始顺序编号,一直到 $n$。有 $m$ 次询问,每次询问第 $x$ 次被打印出来的字符串在第 $y$ 次被打印出来的字符串中出现过多少次。
这道题考察了对 $fail$ 指针的理解。
我们知道若 $fail_x=y$,那么 $y$ 所属的字符串一定是 $x$ 所属的字符串的后缀,换而言之,也就是 $y$ 所属的字符串是 $x$ 所属的字符串的子串。
所以,这道题就变成了,属于模式串 $y$ 的节点中,有多少个节点的 $fail$ 直接或间接的指向 $x$ 的尾节点。
进一步我们可以用 $fail$ 指针构成一棵 $fail$ 树,此时 $fail$ 树的节点还是原 Trie 的节点,但只有 $fail_x$ 连向 $x$ 的边:
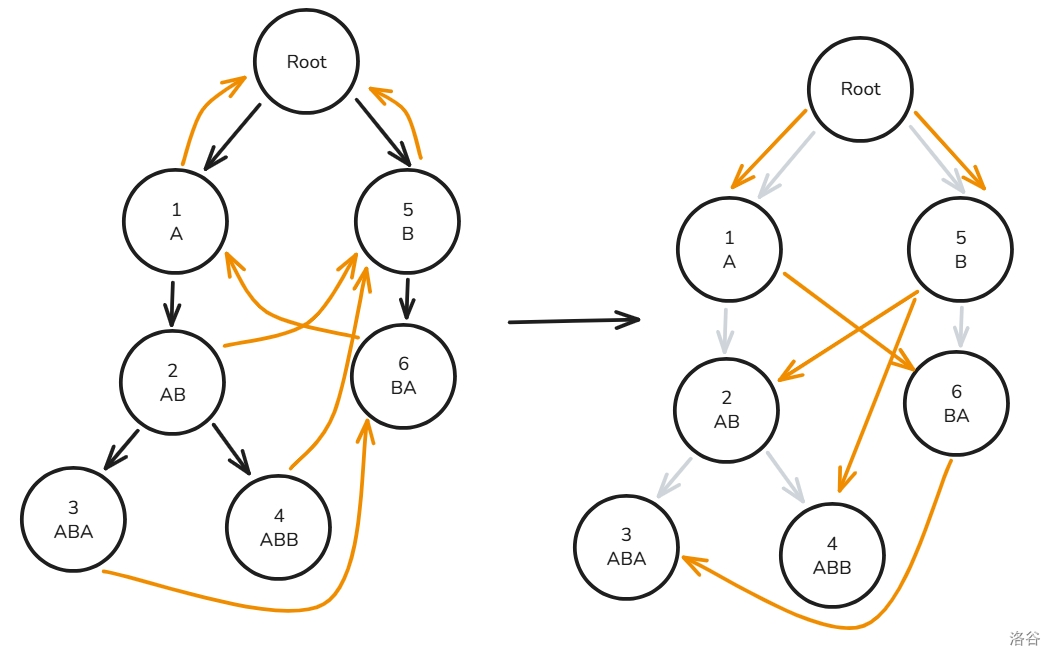
于是,这道题就变成了:在 $fail$ 树中以模式串 $x$ 结尾所在的节点的子树中,有多少个节点在 Trie 中是属于模式串 $y$ 的。
这样看起来似乎还是不太好搞,但是我们知道一条性质:子树内的 $dfn$ 是连续的,我们似乎能通过这个 $dfn$ 来维护信息,而这个可以用树状数组来维护。
我们先将询问 $x,y$ 离线存储到模式串 $x$ 尾节点里,然后呢,我们可以 DFS 整个 $fail$ 树,找到每个节点在 $fail$ 树中所对应的 $dfn$ 和每个子树的大小。
再然后,我们可以再根据输入的信息来模拟:每次输入小写字母时就更新树状数组在 $dfn_x$ 的位置上打上标记,遇到 `B` 时就先将打上的标记撤销,令 $x\gets fa_x$,这个 $fa$ 数组可以在插入模式串时就理好,最后,遇到询问操作 `P` 的时候就直接枚举这个节点存过的询问,一一回答就行了。
时间复杂度:$O(n\log n)$,当然因为常数问题速度跟 $O(n\log^2 n)$ 差不多了。
完整代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
struct node{
int flag,fa,fail,son[30];
}t[100010];
struct Query{
int x,id;
};
int tr[100010],dfn[100010],siz[100010],dep[100010],ans[100010],endpos[100010],cnt=1,pos=1,cntq,tot,q;
vector<int>v[100010];
vector<Query>Q[100010];
int lowbit(int x){
return x&-x;
}
void build(int x,int y){
for(int i=x;i<=cnt+1;i+=lowbit(i)){
tr[i]+=y;
}
return;
}
int query(int x){
int ans=0;
for(int i=x;i;i-=lowbit(i)){
ans+=tr[i];
}
return ans;
}
void insert(char ch){
if(!t[pos].son[ch-'a'])t[pos].son[ch-'a']=++cnt;
t[t[pos].son[ch-'a']].fa=pos;
pos=t[pos].son[ch-'a'];
return;
}
void build_fail(){
for(int i=0;i<26;i++){
t[0].son[i]=1;
}
t[1].fail=0;
queue<int>q;
q.push(1);
while(!q.empty()){
int tmp=q.front();
q.pop();
for(int i=0;i<26;i++){
if(!t[tmp].son[i]){
t[tmp].son[i]=t[t[tmp].fail].son[i];
continue;
}
t[t[tmp].son[i]].fail=t[t[tmp].fail].son[i];
q.push(t[tmp].son[i]);
}
}
return;
}
void build_graph(){
for(int i=1;i<=cnt;i++){
v[i].push_back(t[i].fail);
v[t[i].fail].push_back(i);
}
return;
}
void dfs(int x,int fa){
dfn[x]=++tot,siz[x]=1;
for(int i:v[x]){
if(i==fa)continue;
dfs(i,x);
siz[x]+=siz[i];
}
return;
}
int main(){
string opt;
cin>>opt>>q;
for(char ch:opt){
if(ch=='B'){
pos=t[pos].fa;
}else if(ch=='P'){
t[pos].flag=++cntq;
endpos[cntq]=pos;
}else{
insert(ch);
}
}
build_fail();
build_graph();
dfs(0,-1);
for(int i=1;i<=q;i++){
int x,y;
cin>>x>>y;
Q[endpos[y]].push_back({endpos[x],i});
}
pos=1;
for(char ch:opt){
if(ch=='B'){
build(dfn[pos],-1);
pos=t[pos].fa;
}else if(ch=='P'){
for(Query i:Q[pos]){
ans[i.id]=query(dfn[i.x]+siz[i.x]-1)-query(dfn[i.x]-1);
}
}else{
pos=t[pos].son[ch-'a'];
build(dfn[pos],1);
}
}
for(int i=1;i<=q;i++){
cout<<ans[i]<<endl;
}
return 0;
}
```
## 5.3 P2292 [HNOI2004] L 语言
**提醒:作者这个做法的复杂度时错的,能 AC 纯粹就是靠玄学优化卡过去的。**
> 给定 $n$ 个模式串 $s_i$,定义一个字符串能够被理解为这个字符串可以拆成若干个模式串拼接而成,有 $m$ 次询问,第 $i$ 次询问 $T_i$ 最长能够被理解的前缀子串的长度。\
> $n\le 20,m\le 50,1\le |s|\le 20,\sum_{i=1}^{m}|T_i|\le 10^6$,$s$ 与 $t$ 中均只含小写英文字母。
这题的正解是状压~~但是我没用也过了~~。
我们设朴素的 $dp_i$ 为询问字符串中以第 $i$ 位结尾的子串能否被读懂。
转移的时候只要枚举每个模式串,暴力跳 $fail$ 查询就行了,理论最劣时间复杂度为 $O(n^2\sum|T_i|)$,凭借着庞大的常数成功 TLE。
于是我们可以做几个小优化:
- 在跳 $fail$ 时,如果发现 $dp_i$ 已经为真就直接跳出循环。
- 如果 $dp_{i-mx}$ 到 $dp_i$ 都不为真,那么直接就能跳出循环了($mx$ 为最长的模式串的长度即 $\max_{i=1}^{n}|s_i|$)。
然后这道题就能这样卡过了,完整代码如下:
```cpp
#include<bits/stdc++.h>
using namespace std;
bool dp[2000010];
struct ll{
int son[30],fail,flag;
}t[2010];
int cnt=1;
void build(string s){
int pos=1;
for(int i=0;i<s.size();i++){
if(!t[pos].son[s[i]-'a']){
t[pos].son[s[i]-'a']=++cnt;
}
pos=t[pos].son[s[i]-'a'];
}
t[pos].flag=s.size();
return;
}
void build_fail(){
for(int i=0;i<26;i++)t[0].son[i]=1;
t[1].fail=0;
queue<int>q;
q.push(1);
while(!q.empty()){
int tmp=q.front();
q.pop();
for(int i=0;i<26;i++){
if(!t[tmp].son[i]){
t[tmp].son[i]=t[t[tmp].fail].son[i];
continue;
}
t[t[tmp].son[i]].fail=t[t[tmp].fail].son[i];
q.push(t[tmp].son[i]);
}
}
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int n,m,mx=0;
cin>>n>>m;
for(int i=1;i<=n;i++){
string s;
cin>>s;
build(s);
mx=max(mx,int(s.size()));
}
build_fail();
while(m--){
string s;
cin>>s;
s=' '+s;
fill(dp,dp+s.size(),false);
int pos=1,last=0,ans=0;
bool flag=false;
dp[0]=true;
for(int i=1;i<s.size();i++){
pos=t[pos].son[s[i]-'a'];
int k=pos;
while(k>1){
dp[i]|=dp[i-t[k].flag];
if(dp[i])break;
k=t[k].fail;
}
if(dp[i])last=i;
else{
if(i-last>mx){
ans=last;
flag=true;
break;
}
}
}
if(flag)cout<<ans<<'\n';
else{
for(int i=1;i<s.size();i++){
if(dp[i])ans=i;
}
cout<<ans<<'\n';
}
}
return 0;
}
```
## 5.4 CF547E Mike and Friends
> 给定 $n$ 个字符串 $s_i$ 和 $q$ 次询问,每次询问第 $x_i$ 个字符串在第 $l_i$ 到 $r_i$ 个字符串中的出现次数。
> $1\le n,\sum|s_i|\le 2\times10^5$,$1\le q\le 5\times 10^5$。
首先,我们可以将查询 $s_i$ 在 $l_i$ 到 $r_i$ 的出现次数看成查询 $1$ 到 $r_i$ 减去 $1$ 到 $l_i-1$ 的出现次数。
之后,我们可以将这样拆分出的询问按右端点从小到大排序。
我们在刚刚做过的阿狸的打字机中知道了,一个字符串再另一个字符串中出现的个数,等同于查找一个字符串的尾节点在 $fail$ 树中的子树里包含另一个字符串的节点的个数。
这个东西我们同样可以用 $dfn$ 序来维护。
通过单点修改区间查询的树状数组,我们遍历排序好了的询问,增加右端点时将这个字符串的所有字符在 $fail$ 树上的 $dfn$ 处加 $1$,询问直接求就好了。
时间复杂度:$O(n\log n)$。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
int p[200010],tr[200010],ans[200010],siz[200010],dfn[200010],n,q,cnt=1,cnt2,tot;
string s[200010];
struct ll{
int flag,fail,son[30];
}t[200010];
vector<int>v[200010];
struct query{
int x,y,id;//1->y find x
bool operator<(const query &a)const{
return y<a.y;
}
}Q[200010];
int lowbit(int x){
return x&-x;
}
void update(int pos){
for(int i=pos;i<=cnt2;i+=lowbit(i)){
tr[i]++;
}
return;
}
int query(int x){
int ans=0;
for(int i=x;i;i-=lowbit(i)){
ans+=tr[i];
}
return ans;
}
void insert(string s,int x){
int pos=1;
for(char i:s){
if(!t[pos].son[i-'a']){
t[pos].son[i-'a']=++cnt;
}
pos=t[pos].son[i-'a'];
}
p[x]=pos;
return;
}
void build_fail(){
queue<int>q;
for(int i=0;i<26;i++)t[0].son[i]=1;
q.push(1);
while(!q.empty()){
int tmp=q.front();
q.pop();
// cout<<tmp<<' ';
for(int i=0;i<26;i++){
if(!t[tmp].son[i]){
t[tmp].son[i]=t[t[tmp].fail].son[i];
continue;
}
// cout<<"son:"<<tmp<<' '<<i<<' '<<t[tmp].son[i]<<'\n';
t[t[tmp].son[i]].fail=t[t[tmp].fail].son[i];
q.push(t[tmp].son[i]);
}
}
return;
}
void build_graph(){
for(int i=2;i<=cnt;i++){
v[t[i].fail].push_back(i);
}
return;
}
void dfs(int x){
dfn[x]=++cnt2,siz[x]=1;
for(int i:v[x]){
dfs(i);
siz[x]+=siz[i];
}
}
void addlink(string s){
int pos=1;
for(int i:s){
pos=t[pos].son[i-'a'];
update(dfn[pos]);
}
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>s[i];
insert(s[i],i);
}
build_fail();
build_graph();
dfs(1);
// cout<<"siz:";for(int i=1;i<=cnt;i++)cout<<siz[i]<<' ';cout<<endl;
for(int i=1;i<=q;i++){
int l,r,x;
cin>>l>>r>>x;
Q[++tot]={x,l-1,tot};
Q[++tot]={x,r,tot};
}
sort(Q+1,Q+tot+1);
for(int i=1;i<=tot;i++){
if(Q[i].y==0)continue;
for(int j=Q[i-1].y+1;j<=Q[i].y;j++){
addlink(s[j]);
}
ans[Q[i].id]=query(dfn[p[Q[i].x]]+siz[p[Q[i].x]]-1)-query(dfn[p[Q[i].x]]-1);
}
for(int i=1;i<=q;i++){
cout<<ans[i*2]-ans[i*2-1]<<'\n';
}
return 0;
}
```
## 5.5 CF1437G Death DBMS
> 有 $n$ 个字符串 $s_i$,每个字符串都有一个属于自己的权值,有 $q$ 次询问,每次询问包含:
> - 修改一个字符串 $s_i$ 的权值。
> - 查询一个字符串 $t$ 的所有子串中最大的权值。
>
> $1\le n,q,\sum|s_i|,\sum|t|\le 3\times 10^5$。
同样考察了对 $fail$ 树的运用。
我们来想想 $fail$ 树上一个节点和它的父节点的关系,根据 $fail$ 指针的定义,父节点所代表的字符串一定是这个节点代表的字符串的后缀(读起来有些绕口)。
于是,我们顺着一个节点跳父节点,直到跳到根节点,就能遍历出它的所有后缀。
我们又知道,一个字符串的所有字串等同于它的所有前缀的后缀,于是我们可以枚举字符串的每一个前缀,查找这个前缀跳父节点中经过的节点中最大的权值。
而树上一条链的最大值,不难想到可以用树链剖分来维护。
于是这道题就做完了,复杂度 $O(n\log^2 n)$,下面代码中我用的是 zkw 线段树写的,吸氧后最慢点大约 $420ms$。
(然而这个傻逼卡了半天常被同学发现重链求错了)
代码:
```cpp
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define ls(x) x<<1
#define rs(x) x<<1|1
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
using namespace std;
int tr[1200010],a[300010],p[300010],siz[300010],hev[300010],dep[300010],top[300010],dfn[300010],fa[300010],cnt=1,cnt2,M;
char buf[1<<20],*p1=buf,*p2=buf;
string s[300010];
struct ll{
int fail,son[30];
}t[300010];
multiset<int>st[300010];
vector<int>v[300010];
inline int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9')f=(c=='-'?-f:f),c=getchar();
while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x*f;
}
inline string read2(){
char c=getchar();string s;
while(c<'a'||c>'z')c=getchar();
while(c>='a'&&c<='z')s+=c,c=getchar();
return s;
}
inline void build_zkw(){
M=1;
while(M<=cnt2)M<<=1;
for(int i=1;i<=cnt2;i++){
if(st[i].empty()){
st[i].insert(-1);
tr[M+i-1]=-1;
}else tr[M+i-1]=*(st[i].rbegin());
}
for(int i=M-1;i>=1;i--){
tr[i]=max(tr[ls(i)],tr[rs(i)]);
}
}
inline void update(int p){
int pos=M+p-1;
tr[pos]=*(--st[p].end());
for(pos>>=1;pos;pos>>=1){
tr[pos]=max(tr[ls(pos)],tr[rs(pos)]);
}
}
inline int query_max(int l,int r){
int ans=-1,L=M+l-1,R=M+r-1;
while(L<=R){
if(L&1)ans=max(ans,tr[L++]);
if(!(R&1))ans=max(ans,tr[R--]);
L>>=1,R>>=1;
}
return ans;
}
inline void insert(string s,int x){
int pos=1;
for(char i:s){
if(!t[pos].son[i-'a']){
t[pos].son[i-'a']=++cnt;
}
pos=t[pos].son[i-'a'];
}
return p[x]=pos,void();
}
inline void dfs(int x){
siz[x]=1;
for(int i:v[x]){
fa[i]=x,dep[i]=dep[x]+1;
dfs(i);
if(siz[i]>siz[hev[x]]){
hev[x]=i;
}
siz[x]+=siz[i];
}
return;
}
inline void dfs2(int x){
// cout<<x<<' ';
dfn[x]=++cnt2;
if(!top[x])top[x]=x;
if(hev[x]){
top[hev[x]]=top[x];
dfs2(hev[x]);
}
for(int i:v[x]){
if(i==hev[x])continue;
dfs2(i);
}
return;
}
inline void build_graph(){
for(int i=2;i<=cnt;i++){
v[t[i].fail].push_back(i);
}
return dfs(1),dfs2(1),void();
}
inline void build_fail(){
for(int i=0;i<26;i++)t[0].son[i]=1;
queue<int>q;
q.push(1);
while(!q.empty()){
int tmp=q.front();
q.pop();
for(int i=0;i<26;i++){
if(!t[tmp].son[i]){
t[tmp].son[i]=t[t[tmp].fail].son[i];
continue;
}
t[t[tmp].son[i]].fail=t[t[tmp].fail].son[i];
q.push(t[tmp].son[i]);
}
}
return build_graph(),void();
}
inline int query_link(int x){
int ans=-1;
while(x>1){
ans=max(ans,query_max(dfn[top[x]],dfn[x]));
x=fa[top[x]];
}
return ans;
}
inline int query(string s){
int pos=1,mx=-1;
for(char i:s){
pos=t[pos].son[i-'a'];
// cout<<mx<<' ';
mx=max(mx,query_link(pos));
}
return mx;
}
int main(){
int n=read(),q=read();
for(int i=1;i<=n;i++){
s[i]=read2();
insert(s[i],i);
}
build_fail();
// for(int i=1;i<=cnt;i++){
// cout<<fa[i]<<' '<<top[i]<<' '<<dfn[i]<<endl;
// }
for(int i=1;i<=n;i++){
st[dfn[p[i]]].insert(0);
}
build_zkw();
while(q--){
int op=read(),x,y;
string s;
if(op==1){
x=read(),y=read();
st[dfn[p[x]]].erase(st[dfn[p[x]]].find(a[x]));
st[dfn[p[x]]].insert(y);
a[x]=y;
update(dfn[p[x]]);
}else{
s=read2();
printf("%d\n",query(s));
}
}
return 0;
}
```
# 6. 作业
1. [P3796 AC 自动机(简单版 II)](https://www.luogu.com.cn/problem/P3796)。
2. [P3121 [USACO15FEB] Censoring G](https://www.luogu.com.cn/problem/P3121)。
3. [P4052 [JSOI2007] 文本生成器](https://www.luogu.com.cn/problem/P4052)。
# 7. 闲话
说实话,这篇文章的图画了我很长时间~~尤其是画完之后发现是错的真的崩溃了~~,至于画错的图我也不想补了。
话说我感觉对于 CSP-S 最有用的就是拿 AC 自动机来帮我记 KMP 模板了(当然也有可能我是废物连那个都记不住),而且 CCF 多久没出字符串了。
蒟蒻不才,膜拜大佬,如果文章有任何错字等问题,请在评论区提醒我。