P2283 [HNOI2003]多边形
ecnerwaIa
·
·
题解
题目
半平面交的模板题
以下转载于半平面交算法入门详解(计算几何)
半平面交是什么?
我们知道一条直线可以把平面分为两部分,其中一半的平面就叫半平面。
那半平面交,就是多个半平面的相交部分。我们在学习线性规划时就有用过。
半平面交有什么用?
-
求解一个区域,可以看到给定图形的各个角落。(多边形的核)
-
求可以放进多边形的圆的最大半径。
求解半平面交的步骤(S&I算法 O(nlogn))
我们试着来解决 “求解一个区域,可以看到给定图形的各个角落。”
为了叙述方便,我们把这个区域叫做多边形的核。
1.选取一个正方向。(一般为逆时针)
我们用这个一个不规则图形举例子。
首先我们选逆时针方向做为有向线段。
这样选取的好处是,保证核在有向线段的左边。(可用叉乘判断点与线位置关系)
2.把有向线段通过极角排序(与 x 轴的夹角)(-180°,180°]
排序结果如下所示。
按照极角排序的原因是写代码方便,排序之后的线段是有序的,可以在双端队列里进行操作。(下面会再解释)。
3.按顺序遍历每条线段,取左边区域,删右边区域
我们用这个 S&I 算法求解半平面交时,用的是删减法,首先我们假设全部平面都是半平面交,然后不断加入直线,不断删去右边区域,保留左边区域。最后剩下的区域就是需要求的半平面交。
(1). 全部平面都是半平面交。
(2). 加入第一条直线,保留左边区域,删除右边区域。
(3). 加入第二条线段,保留左边区域,删除右边区域。
(4). 依次加入3 - 10线段,保留左边区域,删除右边区域。
(5). 加入最后一条线段,保留左边区域,删除右边区域。
(6). 剩下的蓝色部分,就是多边形的和,也就是所有直线的半平面交,在蓝色区域的任何一点,都可以看到多边形的每一个角落。
(7).这时我们得到的是围成这个蓝色区域的直线集合。
### 4.如果题目要求求面积。
我们可以发现求出来的直线的集合是有序的 $L=\{2,5,7,9,11\}$ ,这些直线刚好是逆时针围着这个半平面交。(这就是按极角排序的好处)。如果要求面积,我们可以把所有$L[i]$和$L[i+1]$的交点求出来,然后用叉乘求凸包面积。
### 5.总结
总体而言$\ $,$\ $求半平面交其实就是维护线段的集合 $\ $$L$,$\ $遍历每一条线段,判断这条线段加入后对于半平面交的影响,然后在集合$L$中剔除掉对半平面交没有决定作用的边,留下起决定作用的边。即最终目的是维护半平面交的线段集合$L$。
### 6.算法优化
#### 同极角时,排序后可以去掉右边的线段,保留左边的线段。
例如上述步骤 3-3 时,加入第二条线段。不难发现,当①号线段和②号线段的极角相同时,①号线段没有意义。因为①号线段在②号线段右边。因此在排序后,可以去掉没有意义的线段,即保留极角相同的情况下最左边的线段。
### 算法实现 S&I 算法 O(nlogn)
#### 算法流程
1. 以逆时针为正方向,建边。(输入方向不确定时,可用叉乘求面积看正负得知输入的顺逆方向。)
2. 对线段根据极角排序。
3. 去除极角相同的情况下,位置在右边的边。
4. 用双端队列储存线段集合 $L$,遍历所有线段。
5. 判断该线段加入后对半平面交的影响,(对双端队列的头部和尾部进行判断,因为线段加入是有序的。)。
6. 如果某条线段对于新的半平面交没有影响,则从队列中剔除掉。
7. 最后剩下的线段集合 $L$,即使最后要求的半平面交。
### 疑问解答
#### 1.为什么要用双端队列?
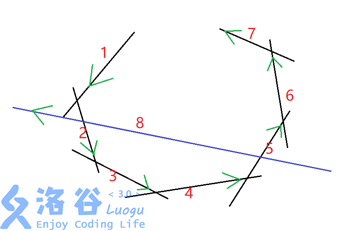
因为线段是按照极角排序的,所以可以形成环,如图,原来的线段集合为
$L=\{1,2,3,4,5,6,7\}$。现在我们想把线段 $8$ 加入到线段集中,显然核的形成和线段$1、6、7$已经没有关系了,因此我们应该在队列的头部找到线段 $1$,把它删去,然后在队列的尾部找到线段$6、7$,然后删除掉。
### 2.线段怎么才对半平面交没有影响?
在下图中,蓝色为当前半平面交。
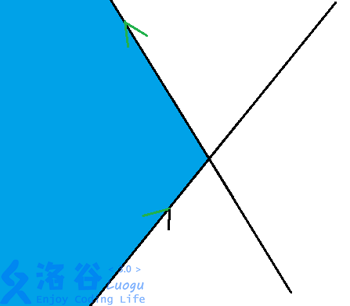
当我们加入红色线段时,半平面交产生了变化。
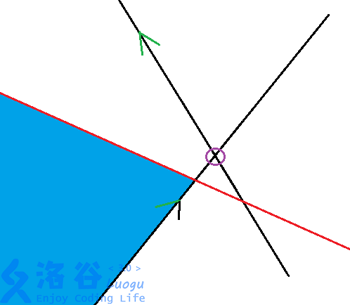
因为我们对线段进行了排序,所以加入的线段会比前面的更“陡”。显然,如果先前的两条线段的交点在当前加入线段的右侧,则较“陡”的那条线段就会无效。
-----
### 注意事项:
1. 点Point,和向量Vector是可以用一个结构体存的,为了好区分,用typedef Point Vector,就可以区分变量是点还是向量了。(头一次发现typedef 还有这种用)
2. 一条直线用一个点和一个向量表示比较方便
3. 关于求给出了一个点和向量的两条直线的交点,最好自己手推下(推导过于简单已省略)
4. 每次加入一个点前弹去队首和队尾在当前直线右边或者在直线上的点,注意可能会有向量相同的线段,此时保留点在左边的线段
5. 最后一定要将队尾的交点和第一条直线比较,如果不在左边,要弹出,直到满足,如图也是合法的,但是队尾和队首却不合法
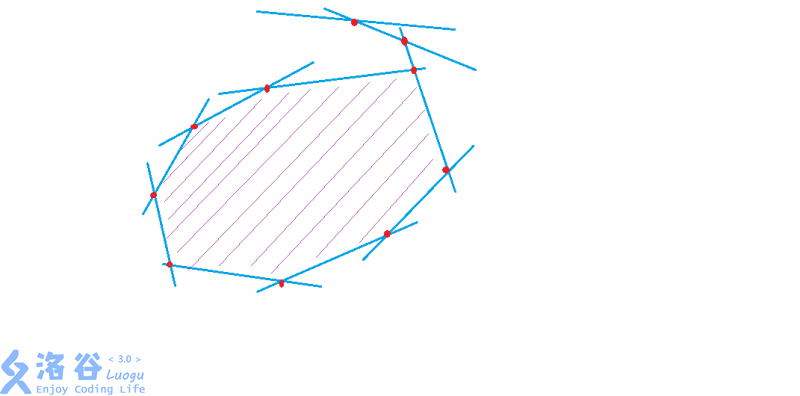
6. 关于求出了所有交点怎么求面积?有$s=\sum_{i=1}^{i=m}{Cross(Point_{i},Point_{i\%m+1})}$(Cross:叉乘)至于证明也不是太难,可以自己尝试着证明一下
下面上代码(因为是第一次写半平面交,所以我几乎是照着楼上题解打的,感觉那样写更简洁)
```cpp
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=1550;
struct Point{
double x,y;
Point(double xx=0,double yy=0){x=xx;y=yy;}
};
typedef Point Vector;
inline Vector operator +(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
inline Vector operator -(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
inline Vector operator *(Vector a,double b){return Vector(a.x*b,a.y*b);}
inline Vector operator /(Vector a,double b){return Vector(a.x/b,a.y/b);}
inline double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}//点乘
inline double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}//叉乘
struct Line{
Point x;Vector y;
double k;
Line(Point a=Point(),Point b=Point()){x=a;y=b;k=atan2(y.y,y.x);}//k:方位角
};
inline bool cmp(Line a,Line b){return a.k<b.k;}//按方位角排序
const double eps=1e-12;
inline double fabs_(double x){return x<0?-x:x;}
inline int dcmp(double x){return fabs_(x)<eps?0:(x>0?1:-1);}
inline bool Onleft(Line a,Point b){return dcmp(Cross(a.y,b-a.x))==1;}
Point a[N],p[N];
Line l[N],q[N];
int n,cnt,m;
inline Point get(Line a,Line b){
Vector c=a.x-b.x;
double t=Cross(b.y,c)/Cross(a.y,b.y);
return a.x+a.y*t;
}int fir,en;
inline void work(){
sort(l+1,l+1+n,cmp);
fir=en=1;q[1]=l[1];
for(int i=2;i<=n;++i){
while(fir<en&&!Onleft(l[i],p[en-1]))en--;
while(fir<en&&!Onleft(l[i],p[fir]))fir++;
q[++en]=l[i];
if(dcmp(Cross(q[en].y,q[en-1].y))==0){
en--;
if(Onleft(q[en],l[i].x))q[en]=l[i];
}
if(fir<en)p[en-1]=get(q[en-1],q[en]);
}
while(fir<en&&!Onleft(q[fir],p[en-1]))en--;
if(en-fir<=1)return;
p[en]=get(q[fir],q[en]);m=en-fir+1;
}inline void slove(){double ans=0;
for(int i=fir;i<en;++i)ans+=Cross(p[i],p[i+1]);
ans+=Cross(p[en],p[fir]);
printf("%.2lf\n",ans/2);
}
int main(){
scanf("%d",&n);
if(n==4){printf("3.46\n");return 0;}
for(int i=n;i>=1;--i)scanf("%lf%lf",&a[i].x,&a[i].y);
for(int i=1;i<=n;++i)l[i]=Line(a[i],a[i%n+1]-a[i]);
work();slove();
return 0;
}
```