题解:P11115 [ROI 2024] 白菜 (Day 1)
Lucyna_Kushinada
·
·
题解
P11115 [ROI 2024] 白菜 (Day 1)
简要题意
给定 n 个矩形。
求有哪些水平线段 [l,r] 满足,出现一个行,满足这一行 l\sim r 都被矩形覆盖,l-1,r+1 没有被覆盖。
并对每个这样的线段求出:
-
有多少行满足满足 l\sim r 都被覆盖,l-1,r+1 没有被覆盖。
-
最长有连续的多少行满足 l\sim r 都被覆盖,l-1,r+1 没有被覆盖。
有多测。
题解
知识点:扫描线,线段树。
怎么没人写题解。
极其折磨的一题,调试难度比较大。
这题可太扫描线了,那就用扫描线吧。
现在决定扫描 x 还是 y 轴。
显然扫描 x 轴,是比较有前途的,毕竟要求的线段都是水平的。
看到坐标值域 10^9,先离散化,对于 y 坐标,每个离散化后的值表示一条线段,对于 x 坐标,则就对应原坐标。
此时有一个显然的 O(n^2) 做法,对每一个离散化后的 y 去扫描 x,如果当前扫到的连续段断了,就计入答案。
显然,题目所提到的线段数量不会超过 n,上面的做法做了不少重复功。
既然扫描的是 $x$ 轴,那就用线段树维护离散化后 $y$ 轴的覆盖情况。
扫描的过程中,至多出现 $n$ 次 $y$ 上一段的覆盖段变为无覆盖段,但是这个段的每个 $y$ 不一定都会贡献给同一条水平线段,如果暴力遍历的话是能很轻易的卡掉的。
定义一个位置从被覆盖变为无覆盖时,才会产生贡献。
那就这样,让中间没有夹杂**贡献其他水平线段**的位置,但是可以夹杂**当前不参与贡献**的位置,贡献相同水平线段的**行连续**位置一起处理掉。
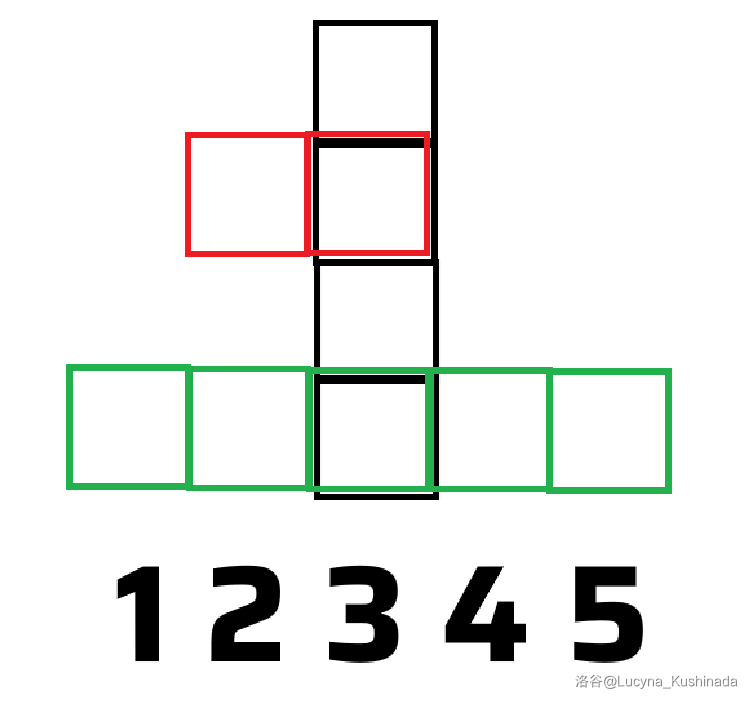
拿图说话,假设现在扫描到了 $x=4$,黑色矩形可以看作一段**行连续**的位置,它夹杂了**贡献其他水平线段**的位置,即红色矩形所在行,贡献的是线段 $[2,3]$,而黑色矩形贡献的是线段 $[3,3]$。
绿色是**当前不参与贡献**的位置,因为它贡献的是线段 $[1,5]$,参照定义,它在扫描到 $x=6$ 时才会贡献。
容易发现这些**行连续**位置组成的段的数量是 $O(n)$ 级别的,终于找到了突破点,如果能在线段树上维护,那也至多拆分成 $O(n \log n)$ 级别。
为了支持这个扫描线的过程,维护有位置从被覆盖到无覆盖时的贡献,考虑一下这棵线段树需要哪些标记:
- $w$:当前区间管控位置中被覆盖层数最小的位置的覆盖层数。
- $tg$:懒标记,该区间被整体增加的层数。
- $ls$:对于当前区间管控位置中被覆盖层数最小的位置,上一次把他们从无覆盖变为覆盖的 $x$。特殊地,如果覆盖层数最小的位置中有来源不同($x$ 不同)的,则为 $0$,显然查询时如果在这里就停下显然会漏数,要向下递归下去。
- $ta$:懒标记,该区间被整体赋值 $ls$ 的位置 $x$。
- $c$:当前区间管控位置中被覆盖层数最小的位置的个数。
以上标记可以解决问题中除了最长连续覆盖以外的部分。
- $lc$:前缀最长覆盖层数为 $w$ 的长度。
- $rc$:后缀最长覆盖层数为 $w$ 的长度。
- $sc$:区间最长覆盖层数为 $w$ 的长度。
- $hc$:如果该区间每个位置覆盖层数均为 $w$,则为区间代表值域上的长度,反之为 $0$。
你会发现上述标记中部分在某个时刻或者某个区间里的值没什么解释意义,但是也无妨,查询函数会出手。
查询时,只在当前区间 $[l,r]$ 被查询区间包含且当前 $ls_k>0$,$w=0$ 才计算整体贡献,这样才会不重不漏,此时标记都是有意义的。
剩下的就是一些细节了,比如跨节点区间的连续段也需要合并;查询的时候是用当前时刻扫描线上 $-1$ 的区间去查的,如果区间有重叠要合并为大区间,防止记重;查询时可能会把一个连续对相同线段贡献的区间拆分为多个小区间,这时候需要手动合并;下传懒标记 $ta$ 的时候要判断能不能传下去。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=(l);i<=(r);++i)
#define per(i,l,r) for(int i=(r);i>=(l);--i)
#define pr pair<int,int>
#define fi first
#define se second
#define pb push_back
#define all(x) (x).begin(),(x).end()
#define sz(x) (x).size()
#define bg(x) (x).begin()
#define ed(x) (x).end()
#define N 402506
// #define int long long
int n,xl[N],yl[N],xr[N],yr[N],lx,ly;
vector<int>vex,vey;
vector<pr>ad[N],dl[N];
struct ln{
int l,r,c,mx;
};
vector<ln>out;
map<pr,pr>ans;
int X,lr,mx,cnt,pre;
struct seg{
#define mid ((l+r)>>1)
int w[N<<2],ls[N<<2],c[N<<2];
int tg[N<<2],ta[N<<2];
int lc[N<<2],rc[N<<2],sc[N<<2],hc[N<<2];
inline void un(int k){
// cout<<"UN "<<k<<' '<<w[k*2]<<' '<<w[k*2+1]<<"\n";
if(w[k*2]<w[k*2+1]){
w[k]=w[k*2];
ls[k]=ls[k*2];
c[k]=c[k*2];
lc[k]=lc[k*2];
rc[k]=0;
sc[k]=sc[k*2];
hc[k]=0;
}
else if(w[k*2]>w[k*2+1]){
w[k]=w[k*2+1];
ls[k]=ls[k*2+1];
c[k]=c[k*2+1];
lc[k]=0;
rc[k]=rc[k*2+1];
sc[k]=sc[k*2+1];
hc[k]=0;
}
else if(w[k*2]==w[k*2+1]){
w[k]=w[k*2];
c[k]=c[k*2]+c[k*2+1];
lc[k]=max(lc[k*2],hc[k*2]?hc[k*2]+lc[k*2+1]:0);
rc[k]=max(rc[k*2+1],hc[k*2+1]?hc[k*2+1]+rc[k*2]:0);
sc[k]=max({sc[k*2],sc[k*2+1],rc[k*2]+lc[k*2+1]});
hc[k]=hc[k*2]&&hc[k*2+1]?hc[k*2]+hc[k*2+1]:0;
if(ls[k*2]==ls[k*2+1]){
ls[k]=ls[k*2];
}
else{
ls[k]=0;
}
}
}
inline void addt(int k,int d,int x){
tg[k]+=d;
w[k]+=d;
if(x){
ls[k]=x;
ta[k]=x;
}
}
inline void pd(int k){
addt(k*2,tg[k],w[k*2]+tg[k]==w[k]?ta[k]:0);
addt(k*2+1,tg[k],w[k*2+1]+tg[k]==w[k]?ta[k]:0);
tg[k]=ta[k]=0;
}
inline void build(int k,int l,int r){
tg[k]=ta[k]=0;
if(l==r){
w[k]=ls[k]=0;
c[k]=lc[k]=rc[k]=sc[k]=hc[k]=vey[l+1]-vey[l];
// cout<<lc[k]<<"\n";
return;
}
build(k*2,l,mid);
build(k*2+1,mid+1,r);
un(k);
}
inline void upd(int L,int R,int k,int l,int r,int x){
if(L<=l&&R>=r){
if(x){
addt(k,1,w[k]?0:x);
}
else{
addt(k,-1,0);
}
return;
}
pd(k);
if(L<=mid){
upd(L,R,k*2,l,mid,x);
}
if(R>mid){
upd(L,R,k*2+1,mid+1,r,x);
}
un(k);
}
inline void ask(int L,int R,int k,int l,int r,int ed){
if(w[k]){
return;
}
if(L<=l&&R>=r&&!w[k]&&ls[k]){
if(X!=ls[k]||lr+1!=l){
if(X){
// cout<<"adda "<<X<<' '<<ed<<' '<<cnt<<' '<<mx<<"\n";
out.pb({X,ed,cnt,mx});
}
X=ls[k],cnt=c[k],mx=sc[k],pre=rc[k];
}
else{
mx=max({mx,pre+lc[k],sc[k]});
pre=max({rc[k],hc[k]?pre+hc[k]:0});
cnt+=c[k];
}
lr=r;
return;
}
if(l==r){
return;
}
pd(k);
if(L<=mid){
ask(L,R,k*2,l,mid,ed);
}
if(R>mid){
ask(L,R,k*2+1,mid+1,r,ed);
}
}
#undef mid
}t;
inline void sol(){
vex.clear();
vey.clear();
out.clear();
ans.clear();
rep(i,0,lx){
ad[i].clear();
dl[i].clear();
}
cin>>n;
rep(i,1,n){
cin>>xl[i]>>yl[i]>>xr[i]>>yr[i];
xr[i]++;
yr[i]++;
vex.pb(xl[i]);
vex.pb(xr[i]);
vey.pb(yl[i]);
vey.pb(yr[i]);
}
sort(all(vex));
vex.erase(unique(all(vex)),ed(vex));
lx=sz(vex);
vex.insert(bg(vex),0);
sort(all(vey));
vey.erase(unique(all(vey)),ed(vey));
ly=sz(vey);
vey.insert(bg(vey),0);
rep(i,1,n){
xl[i]=lower_bound(all(vex),xl[i])-bg(vex);
xr[i]=lower_bound(all(vex),xr[i])-bg(vex);
yl[i]=lower_bound(all(vey),yl[i])-bg(vey);
yr[i]=lower_bound(all(vey),yr[i])-bg(vey);
// cout<<xl[i]<<' '<<yl[i]<<' '<<xr[i]<<' '<<yr[i]<<"\n";
ad[xl[i]].pb({yl[i],yr[i]-1});
dl[xr[i]].pb({yl[i],yr[i]-1});
}
ly--;
t.build(1,1,ly);
rep(i,1,lx){
// cout<<i<<" st\n";
for(pr u:ad[i]){
// cout<<i<<" add1 "<<u.fi<<' '<<u.se<<"\n";
t.upd(u.fi,u.se,1,1,ly,i);
}
for(pr u:dl[i]){
// cout<<i<<" del1 "<<u.fi<<' '<<u.se<<"\n";
t.upd(u.fi,u.se,1,1,ly,0);
}
// cout<<"inf "<<t.w[1]<<"\n";
sort(all(dl[i]));
int nowl=0,nowr=0;
for(pr u:dl[i]){
if(u.fi>nowr+1){
if(nowr){
X=0;
// cout<<nowl<<' '<<nowr<<" ask\n";
t.ask(nowl,nowr,1,1,ly,i);
if(X){
// cout<<"addb "<<X<<' '<<i<<' '<<cnt<<' '<<mx<<"\n";
out.pb({X,i,cnt,mx});
}
}
nowl=u.fi;
}
nowr=max(nowr,u.se);
}
if(nowr){
X=0;
// cout<<nowl<<' '<<nowr<<" ask\n";
t.ask(nowl,nowr,1,1,ly,i);
if(X){
// cout<<"addc "<<X<<' '<<i<<' '<<cnt<<' '<<mx<<"\n";
out.pb({X,i,cnt,mx});
}
}
}
for(ln u:out){
// cout<<u.l<<' '<<u.r<<' '<<u.c<<' '<<u.mx<<"\n";
ans[{u.l,u.r}].fi+=u.c;
ans[{u.l,u.r}].se=max(ans[{u.l,u.r}].se,u.mx);
}
cout<<sz(ans)<<"\n";
for(auto u:ans){
cout<<vex[u.fi.fi]<<' '<<vex[u.fi.se]-1<<' '<<u.se.fi<<' '<<u.se.se<<"\n";
}
}
signed main(){
// freopen("lucyna.in","r",stdin);
// freopen("kushinada.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int t;
cin>>t;
while(t--){
sol();
}
return 0;
}
```