题解：AT_iroha2019_day4_l ...好きです

DengStar · 2025-05-09 22:37:27 · 题解

在我的博客中查看

先考虑静态问题。先把绝对值拆开，只考虑询问左边的点，反过来的情况类似。容易想到在平面直角坐标系上考虑。考虑每个点对答案的贡献。对于点 (x, y) 和询问 x_{0} > x，这个点对答案的贡献相当于使答案对 \dfrac{y}{x_{0} - x} 取 \max。把一个点的贡献看作关于 x_{0} 的函数，则相当于平面有若干个函数图象，每个点 (x_{0}, 0) 的答案就是它正上方的点中纵坐标最大的。x_{0} 在分母不好做，所以取个倒数变成 \dfrac{x_{0} - x}{y}，这是关于 x_{0} 的一次函数

于是问题就变成了：

平面上有若干条直线，多次给定 x_{0}，求出直线上的点中，横坐标为 x_{0} 的点中纵坐标为正数且最小的。

把操作和询问的 x 坐标一起从小到大排序（操作的 x 相当于对应直线的零点），逐个处理。维护加入直线的最小值构成的函数。这么做保证了考虑到的直线在 x = x_0 处一定为正。由于一次函数是上凸的，根据经典结论，一堆一次函数的 \min 仍然上凸，所以直线的最小值构成一个上凸包：

注意到上凸包有以下性质：

• 随着 x 坐标的增大，使得 y 最小的直线斜率单调递减。

所以我们考虑维护一个单调栈，从栈底到栈顶从小到大存放直线的斜率，并且保证栈中每一条直线都存在某个位置，使得这堆直线中的最小值在此直线取到（也就是说保证每条直线都是凸包的一部分）。

加入一条新直线 l 时，讨论它与栈顶直线的关系。有两种情况：

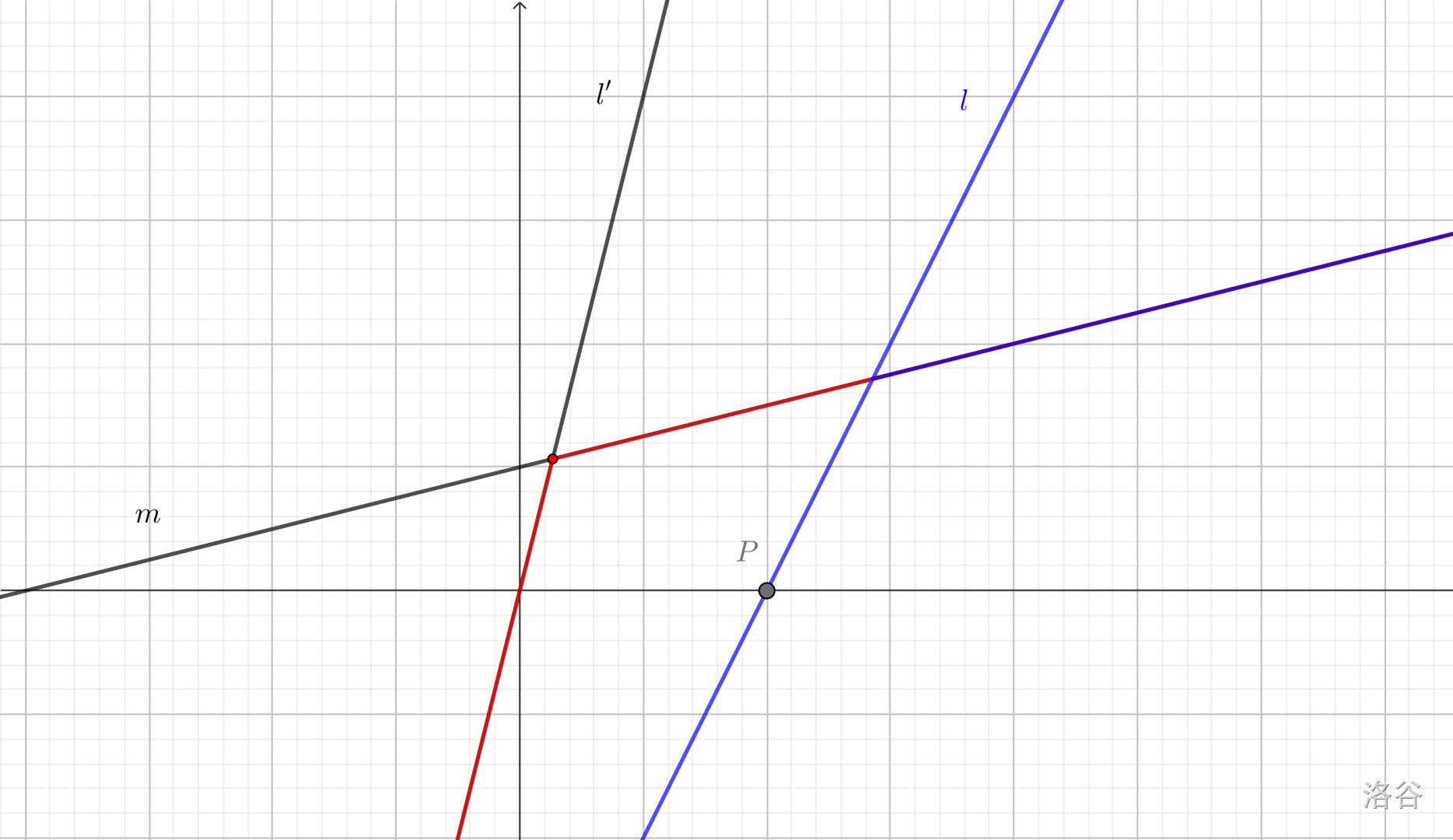1.  如图，$l$ 是新加入的直线。由于 $l$ 的斜率小于 $l'$ 的斜率，所以对于 $P$ 点右侧的询问，$l$ 的纵坐标一定小于 $l'$ 的纵坐标，因此 $l'$ 被弹出。但直线 $m$ 被保留了。
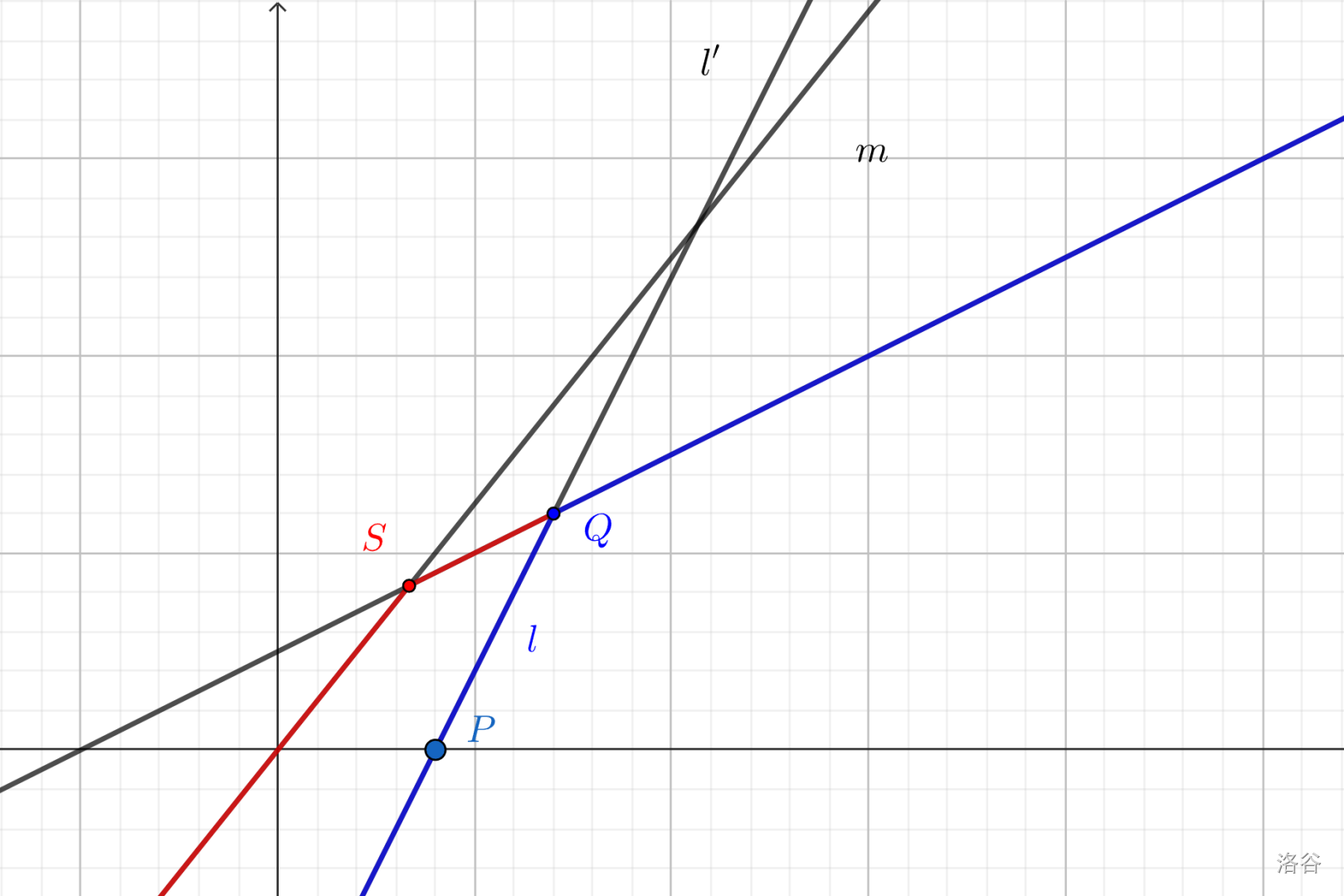2.  如图，虽然 $l$ 的斜率大于栈顶 $l'$ 的斜率，但是由于 $l$ 和 $l'$ 的交点 $Q$ 在 $l'$ 与 $m$ 的交点 $S$ 左侧，所以对于 $P$ 右侧的询问，纵坐标最小值不可能在 $l'$ 取到，这种情况我们也需要弹栈。

以上就讨论完了加入直线的情况。下面考虑如何处理询问。根据凸包的性质，随着 x 坐标的增大，使得 y 最小的直线斜率单调递减。而栈中的直线斜率已经有序，且询问的 x_0 也有序，所以只要比较栈顶和次栈顶在 x_0 处的纵坐标哪个小，如果次栈顶更小，就弹栈。重复这个过程知道栈顶在 x_0 处纵坐标最小，此时栈顶的纵坐标就是答案。

现在静态问题就解决了，时间复杂度为 O(n \log n)，瓶颈在排序，计算答案的过程是线性的。下面考虑动态问题。

对时间轴建立线段树。还是把操作和询问按 x 坐标排序，然后预处理出每条直线出现的时间区间 [l, r]，对于 [l, r] 在线段树上拆分出的 O(\log n) 个区间，把直线加入到这个区间内，按静态问题的方法维护每个区间的凸包。查询 x_{0} 时，对于线段树上包含 x_{0} 的 O(\log n) 个区间，分别计算答案然后取 \min。由于 x 坐标有序，所以正确性可以保证。至于时间复杂度，每条直线在 O(\log n) 个线段树上的区间出现，所以所有区间直线的总数为 O(\log n)。用单调栈计算答案的过程是线性的，所以总时间复杂度还是 O(n \log n)。

代码实现非常清晰：Code

下面附上我写的 generator 供大家调试，可以自行修改数据范围。为了方便，使用了 vector.erase() 用来完成从 set 中随机选取元素的过程，时间复杂度比较劣，但实测生成大数据也很快。（实际上更好的做法是把删除的元素和 vector.back() 交换，然后 pop_back()。）

（在文首链接查看）