题解:AT_joisc2019_e ふたつの料理 (Two Dishes)
P2441M
·
·
题解
题意
有两道菜,做第一道菜有 n 个步骤,完成第 i 步需要 a_i 分钟,做第二道菜有 m 个步骤,完成第 j 步需要 b_j 分钟。两道菜的步骤可以交替执行,中途不能休息。
若你在 s_i 分钟内完成第一道菜的第 i 步,则获得 p_i 分。若你在 t_j 分钟内完成第二道菜的第 j 步,则获得 q_j 分。求做完两道菜后的最大得分。
## 题解
对 $a,b$ 做前缀和,容易得到一个 $\mathcal{O}(nm)$ 的 DP:令 $f_{i,j}$ 表示第一道菜做了前 $i$ 步,第二道菜做了前 $j$ 步,能获得的最大的分。转移枚举最后一步做的是哪一道菜:
$$
f_{i,j}\gets\max(f_{i,j},f_{i-1,j}+[a_i+b_j\leq s_i]p_i)\\
f_{i,j}\gets\max(f_{i,j},f_{i,j-1}+[a_i+b_j\leq t_j]q_j)
$$
预处理 $c_i$ 表示最大的 $j$ 使得 $b_j\leq s_i-a_i$,$d_j$ 表示最大的 $i$ 使得 $a_i\leq t_j-b_j$。自然地放到平面上考虑,将所有 $(i,c_i)$ 和 $(d_j,j)$ 标为关键点。考虑一条从 $(0,0)$ 到 $(n,m)$ 的路径,发现问题可以转化成:若点 $(i,c_i)$ 在路径的上方(非严格)则可以获得 $p_i$ 分,若点 $(d_j,j)$ 在路径的下方(非严格)则可以获得 $q_j$ 分,最大化得分。如下图所示。
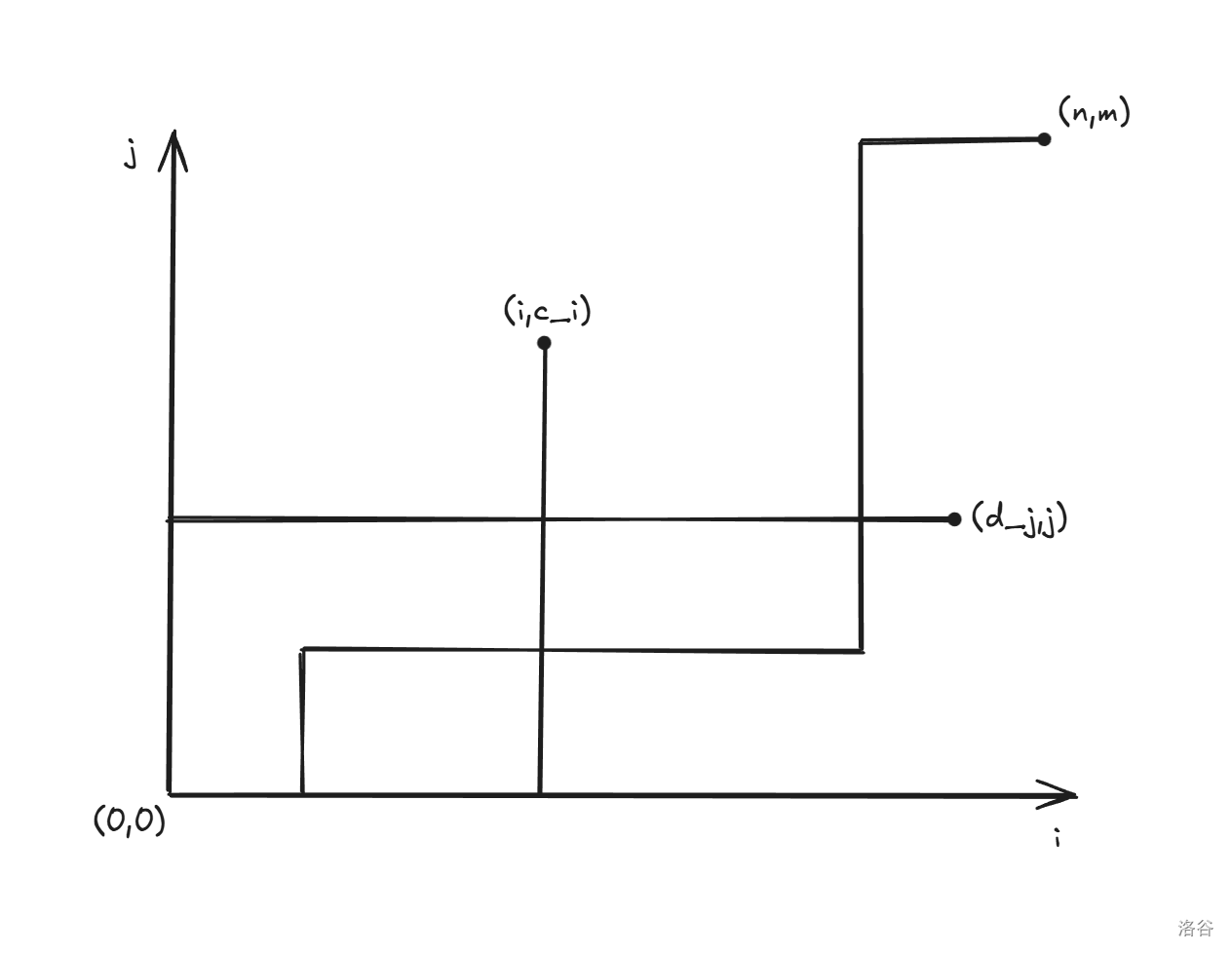
考虑统一一下方向,先令答案为 $\sum p_i$,那么变成若点 $(i,c_i)$ 在路径的下方(严格)则可以获得 $-p_i$ 分,然后将 $(d_j,j)$ 向右下移动变为 $(d_j+1,j-1)$。问题转化成最大化路径下方(严格)的点权。
考虑此时的 DP:令 $f_{i,j}$ 表示从 $(0,0)$ 走到 $(i,j)$,路径下方的最大点权和。设 $w_{i,j}$ 为 $(i,j)$ 处的点权总和,$S_{i,j}=\sum\limits_{k=0}^{j-1}w_{i,k}$ 为 $(i,j)$ 下方的点权总和。转移在向右走时累加下方点权和:
$$
\begin{align*}
f_{i,j}&\gets\max(f_{i,j},f_{i,j-1})\\
f_{i,j}&\gets\max(f_{i,j},f_{i-1,j}+S_{i,j})
\end{align*}
$$
注意由于一些点向右下方移动了一个单位,最终答案应为 $f_{n,m}+S_{n+1,m}$。
DP 的转移变得比较优美了,考虑整体 DP 优化。我们将 $i$ 这一维压掉,那么转移相当于先对于每个 $1\leq j\leq m$,令 $f_j\gets f_j+S_{i,j}$,再对 $f$ 做一次前缀 $\max$。考虑维护差分数组 $g_j=f_j-f_{j-1}$,此时第一步操作变为对于每个 $1\leq j\leq m$,令 $g_j\gets g_j+w_{i,j-1}$,而 $w_{i,j}$ 有值的位置只有 $\mathcal{O}(n+m)$ 个,这很不错。
考察取前缀最大值的过程在差分数组上的表现。依次考虑 $f$ 的每个前缀最大值 $f_{p_1}\leq\cdots\leq f_{p_k}$:将 $g_{p_1+1\sim p_2-1}$ 置为 $0$,令 $g_{p_2}\gets \sum\limits_{k=p_1+1}^{p_2}g_k$,将 $g_{p_2+1\sim p_3-1}$ 置为 $0$……可以发现这个过程等价于令 $t=p_{i}+1,sum=0$,不断执行以下操作:
- 令 $sum\gets sum+g_t$。
- 若 $sum\geq 0$,则令 $g_t\gets sum$,停止操作。
- 否则令 $g_t\gets 0$,$t\gets t+1$。
用 `map` 维护 $g$ 的非 $0$ 项,每次在 $x$ 的位置单点操作后,从该位置开始向后执行上述操作即可。显然除了最后一个位置,被遍历的位置都会被删除,时间复杂度为 $\mathcal{O}((n+m)\log(n+m))$。