证明 Tarjan 求强连通分量的正确性
mwz3
·
·
算法·理论
零:前言
Tarjan 是个神奇的算法。
个人理解,Tarjan 相较于那些直观的算法(如线段树、平衡树),虽然代码简洁,但是背后的原理要难得多。
在网上鲜有 Tarjan 的严格证明,所以笔者就写了这篇文章。
注意,本文仅讨论 Tarjan 求强连通分量的正确性。
本文参考了 OI-wiki 和 Alex_Wei 的博客,在此向他们表示感谢。
一:代码回顾
Tarjan 求强连通分量主要为以下实现。
int dfn[N+1],low[N+1];
int cnt=0;
stack<int>st;
int in_stack[N+1];
vector<int>scc[N+1],scc_cnt=0;
void tarjan(int x){
dfn[x]=++cnt;
low[x]=cnt,in_stack[x]=1;
st.push(x);
for(auto y:a[x]){
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
}else if(in_stack[y])
low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x]){
scc_cnt++;
while(st.top()!=x){
scc[scc_cnt].push_back(st.top());
st.pop();
}
scc[scc_cnt].push_back(st.top());
st.pop();
}
}
在代码运行完成以后,每一个 scc 中存放的都是一个强连通分量。
我们注意到其中关键的两个数组是 dfn 和 low 数组。
$low(x)$ 记录的是如下两种点的 $dfn$ 的最小值:
+ $x$ 本身
+ 从 $x$ 子树内的点起跳,一步能跳到的**在栈内**的点
特别注意这个在栈内,特别注意这个在栈内。
## 二:概述,及性质
首先,明确这篇文章的目标:
证明 Tarjan 求出的所有待证明的 SCC 都确实是 SCC。
那么我们要一个一个来证明吗?不是的。我们可以采用**归纳法**。
我们以每个待证明的 SCC **被弹出的时间**对待证明的 SCC 进行排序。
假设现在待证明的 SCC 为 $A$,利用归纳法,我们可以假设排在它**前面**的待证明的 SCC 都已经被证明是 SCC。根据归纳,如果 $A$ 为 SCC,那么所有待证明的 SCC 都是 SCC。
我们想证明 $A$ 是 SCC,那么要证明两件事情:
- $A$ 中的节点强连通。(强连通性)
- 不能再选出其他节点 $nxt$,使得 $A\cup nxt$ 强连通。(极大性)
#### 基本定义和性质:
- Tarjan 函数深度优先搜索构成的树称为 **dfs 树**。树中的边称为**树边**。
- 与树边相对的,还有**返祖边、横叉边、前向边**。返祖边指返回祖先的边,前向边指指向后代的边,横叉边指其余的边。
- 性质一:设某条返祖边或横叉边为 $u\to v$,一定有 $dfn(v)<dfn(u)$。
+ 证明:若 $dfn(v)>dfn(u)$,那么 dfs 肯定是先递归到 $u$ 再递归到 $v$。在先递归到 $u$ 时,就确定了一点:$v$ 在 $u$ 的子树中,因为 $u\to v$ 这条边存在。
+ 那么有读者就要问了:$u\to v$ 又不一定是树边,为什么 $v$ 一定在 $u$ 的子树中呢(如下图)?
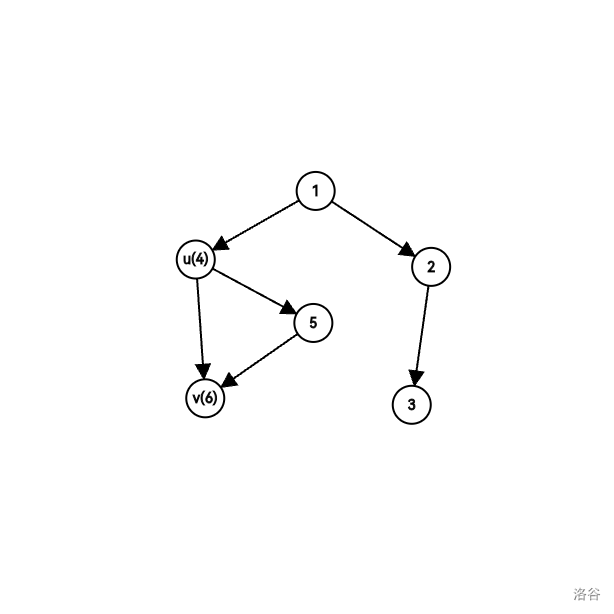
+ 回答是:有机会比 $u$ 抢先访问 $v$ 的**一定只能是 $u$ 的后代**。因为如果后代不访问,$u$ 就自己访问掉了。
+ 因此我们推导出了矛盾:$v$ 在 $u$ 的子树中,但 $u\to v$ 又是横叉边或返祖边。性质一得证。
- 性质二:如果 $x$ 是 $y$ 的后代,那么 $dfn(x)>dfn(y)$。
+ dfs 性质易证。
- 性质三:一个点 $x$ 能到达一个连通块 $A$ 中的所有点与能到达 $A$ 中深度最小的点 $tp$ 等价。我们来证明一下充分性和必要性。
+ 必要性:如果 $x$ 到达不了 $tp$,那么 $x$ 到达不了 $tp$。~~废话。~~
+ 充分性:如果 $x$ 能到达 $tp$,那么由于 $tp$ 是深度最小的那个点,所以 $tp$ 能到达 $A$ 中的所有点,那么 $x$ 就能到达 $A$ 中的所有点。
- 性质四:$x$ 被弹出时 $x$ 的整个子树都一定不在栈内。
+ 证明:$x$ 的所有子树内的点都在 $x$ **之后**入栈,如果 $x$ 被弹出,那么之后入栈的一定被弹出。
- 性质五:所有 dfs 求出来的待证明的 SCC 在树上都是**弱连通块**。
+ 证明:如果 $x$ 在栈内,那么从根到 $x$ 的整条路径上的点都在栈内(性质四),所以我们可以看出**栈内**的点是一个弱连通块。由于我们弹栈是弹出一颗子树,那么把弱连通块割一刀还是弱连通块。
- 性质六:在 $x$ 被弹出时,**在被访问过的点中** $dfn$ 比 $x$ 大的只可能是 $x$ 中的子树中的点。
+ 证明:如果 $dfn$ 比 $x$ 大,那么肯定是在 $x$ 之后被访问,但是从 $x$ 被访问到 $x$ 被弹出之间的只有 $x$ 子树内的节点。
## 三:证明强连通性
假设我们现在待证明的 SCC 为 $A$,其中深度最小的点为 $tp$(性质五,表明只有一个深度最小的点)。
#### 一句话概括:$A$ 中的每个点通过子树一定能访问到 能到达 $tp$ 的点。(读者可以自己考虑如何证明它,以下是详细的证明过程,可以选择略过)
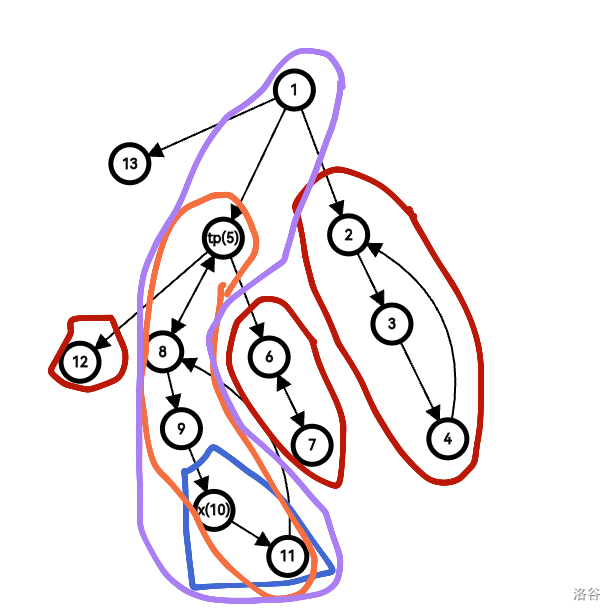
(在图中,红色的表示已经处理完成的强连通分量,蓝色代表 $x$ 的子树,橙色代表连通块 $A$,紫色代表栈内。我们已经证明了 $5,8,9$ 能到达 $tp$,需要证明 $10$。由于 $low(10)\neq dfn(10)$ 且 $low(10)\ge dfn(5)$,那么 $10$ 的子树中一定会有一条边指向 $5,8,9$,图中即为 $11\to 8$。)
由于性质五,$tp$ 能够到达 SCC 中的所有点,**所以只要证明了所有 SCC 内的节点能到达 $tp$ 就做完了。**
**我们有的条件:** 我们有 $low(tp)=dfn(tp)$(弹栈时的判断条件),以及对于 $A$ 中的非 $tp$ 的节点 $x$ 有 $low(x)<dfn(x)$(不然就直接先弹掉了)。
我们**按照 $dfn$** 考虑 $A$ 中的非 $tp$ 的节点 $x$(其实是又一个归纳法):
- **对于 $low(x)$ 的限制:** $dfn(x)\neq low(x)$ 且 $low(x)\ge dfn(tp)$。
- **根据 $low(x)$ 的定义,$low(x)$ 与从 $x$ 子树出发的一条终点在栈内且最小的边 $u\to v$ 是等价的。也就是说,存在一条边满足 $dfn(v)<dfn(x)$ 且 $dfn(v)\ge dfn(tp)$ 且 $v$ 在栈中。**
- 那么 $v$ 一定是能到达 $tp$ 的点(**即归纳法中已经确定能到达 $tp$ 的点**)吗?一定是的。
- 原因是性质六。性质六表明了,$v$ 不可能是在 $tp$ 子树之外的点。那么既然 $v$ 在子树内,并且 $dfn(v)>dfn(x)$,并且 $v$ 在栈中,那么 $v$ 一定从属于 $A$,并且在 $x$ 之前被证明能到达 $tp$。
本部分证毕。
## 四:证明极大性
有人可能会问:不是 $low(tp)=dfn(tp)$ 吗?那么子树内的点都不会连向外界,那不就证完了吗?
**这是错的。原因是 $low$ 的条件是在栈内。$x$ 子树内的节点可以连向已经完成的强连通分量。**
假设我们现在待证明的 SCC 为 $A$。
我们首先对于所有点分个类。
设当前被弹出的待证明的 SCC 为 $A$,已经完成的 SCC 组成的集合为 $B$,还未 dfs 到的点组成的集合为 $C$,剩下的点(**即在 $A$ 被弹出后栈中的点**)组成的集合为 $D$。四个集合两两交集为空,并集为整颗树。
我们假设 $A$ 中要加入的点为 $nxt$。
- $nxt\in B$。
+ 此时 $A$ 中的所有点都能到达 $nxt$,$nxt$ 能到达 $B$ 中的所有点,那么 $A$ 和 $B$ 合并在一起可以构成一个更大的强连通分量,与 $B$ 的极大性产生了矛盾。
- $nxt\in C\cup D$。
+ 下文的 $E_1$ 能**直接**到 $E_2$ 均指原图中存在一条边 $u\to v$,满足 $u\in E_1$ 且 $v\in E_2$。
+ 首先确定一点,没有 $A\to D$ 的**直接**边,原因是 $low(tp)=dfn(tp)$。也没有 $A\to C$ 的**直接**边,原因是性质一。
+ 只要我们证明了 $B$ **直接**到达不了 $C$ 并且 $B$ **直接**到达不了 $D$,就证明了 $A$ 到达不了 $C\cup D$。
+ 证明 $B$ **直接**到达不了 $C$:
+ $C$ 中的点的 $dfn$ 均大于 $B$,所以横叉边和返祖边不行(性质一),而 $B$ 中每个 SCC 的 $tp$ 的子树又已经全部被访问过了,所以前向边和树边都不行。
+ 证明 $B$ **直接**到达不了 $D$:
+ 假设 $B$ 能到达 $D$,路径是 $u\to v$,并且 $u$ 属于强连通分量 $U$。
#### 一句话概括:此时 $U$ 不是极大的,产生了矛盾。
+ $v$ 一定不在强连通分量 $U$ 中,并且在**弹出 $U$ 时**,$v$ 不在任何强连通分量中(因为在**弹出 $A$ 时**它仍不在任何一个强连通分量中)。因为 $U$ 的 $tp$ 的子树内的点均已存在于强连通分量中,$u\to v$ 一定只能是返祖边或横叉边,所以有 $dfn(v)<dfn(u)$。
+ 那么,由于在弹出 $A$ 时 $v$ 在栈内,那么弹出 $U$ 时,$v$ 也在栈内(一个点**入栈出栈仅一次**,弹出 $U$ 比搜索到 $u$ 要晚,而搜索到 $u$ 比搜索到 $v$ 要晚,所以弹出 $U$ 时 $v$ 已入栈)。在弹出 $U$ 时,$v$ 在栈内,并且其子树中有一条 $u\to v$ 的边,并且 $v$ 在子树外,根据性质六,这和 $low(tp)=dfn(tp)$ 产生了矛盾。
因此本部分证毕。
所以全部证毕。