健将青蛙……
HBWH_zzz
·
·
题解
题意
自己看
任务 1
给定 a,b,输出 a+b。
发现 c_1=6,我们显然得考虑常数空间的做法。由于我们只有 +1/-1 操作,所以我们得构造一个结构使得它可以被循环进行。
不难想到构造一个循环,使得 a++ 和 b-- 均在循环内,那么我们可以不断进行这个循环直到 b=0。(对应下图中 (2,2)\sim (3,3) 的区域)
这个循环用 3\times 3 的空间是容易构造的,稍微压一下就是 2\times 3 的了。
在每个任务中,我们都给出 C++ 代码来辅助理解。
int solve(){
while(b)
b--,a++;
return a;
}
比较变量和 0 的大小可以拿出一个无关的内存条来比较,例如下图中的 b>0 比较的是 02>03。
任务 2
给定 a,输出 2^a。
$i\leftarrow 2\times i$ 可以先复制一份 $i$ 再做任务 $1$ 中的 $a+b$。
这个东西比较难压进 $9$ 格,我们可爱的验题人曾经给出过 $4\times 5$ 的答案,最终在 csacdemy 的帮助下成功得到第一版 $c_2=12$ 的答案。
```cpp
int solve(){
int i=1,j=0;
while(a>j){
int k=0;
while(i>k)
++k;
while(k)
--k,++i;
++j;
}
return i;
}
```
这里提一嘴,`c 1 1 x x` 可以作为强迫机器人向某个方向移动的指令。
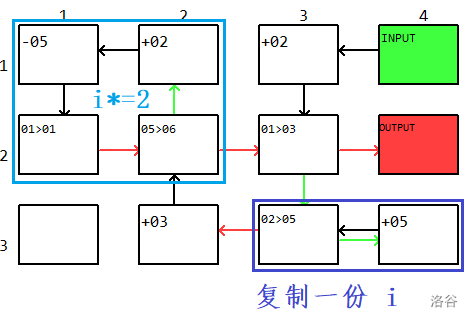
考虑更小的做法。我们需要去掉复制的过程,这一点需要一个人类智慧的做法:设变量 $j=0,i=2^x$,不断让 $j\leftarrow j+2,i\leftarrow i+1$,直到 $j\geq i$。我们稍微压一压就能进 $2\times 5$。
```cpp
int solve(){
int i=0;
while(a>=0){
--a;
int j=0;
do{
++j,++j,++i;
}while(i>j);
}
return i;
}
```

验题人给出了一种类似的实现。
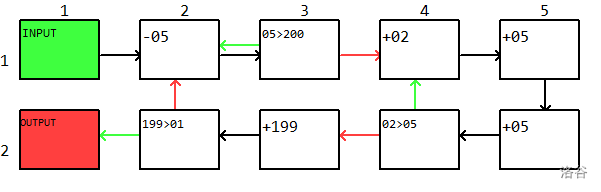
要想网格更小,则需要我们在上图最右侧的 $2\times 2$ 的区域下功夫。我们发现 $\times 2$ 这个操作我们使用了三个自增来实现,这代价是昂贵的。所以我们考虑以下过程 $j=i$,并执行 $j\leftarrow j-1,i\leftarrow i+1$ 直到 $j=0$。这样我们就可以在循环中只使用 $2$ 个 $+-$ 格点。
```cpp
int solve(){
int i=0,j=0;
while(a>=0){
do{
--j,++i;
}while(j>0);
j=i;
--a;
}
return i;
}
```
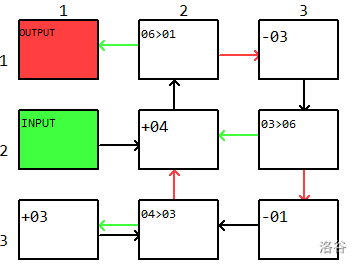
## 任务 $3
给定 a,输出 a^2。
这样的操作很容易压进 $2\times 5$,具体操作类似任务 $2$ 的 $2\times 5$。
```cpp
int solve(){
int i=0,cnt=0;
while(a>cnt){
cnt++;
int j=0;
while(j<a)
++j,++i;
}
return i;
}
```
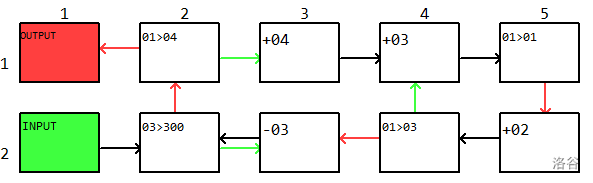
$c_1=9$ 也与任务 $2$ 类似。
```cpp
int solve(){
int i=0,cnt=0;
while(a>cnt){
int j=a;
while(j>0)
--j,++i;
cnt++;
}
return i;
}
```
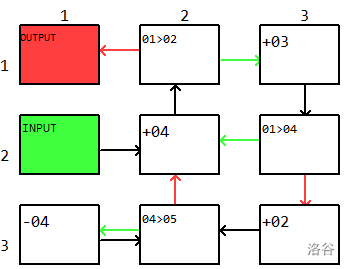
## 任务 $4
给定 a,b,求 a\oplus b。
这是本题的第一个难点。c_1=35 几乎劝退了所有 \log 级别的算法,我们还得继续想 O(1) 的空间。
这时我们想到一个思路:每次挑出一个二进制位比较,算出这一位的答案后清空 a,b 的该位,这样我们就可以不断重复该过程直到 a=b=0。
但是这一位如何选成为了问题。一个聪明的解决方案是每次挑出 \max(a,b) 的最高位进行比较,这样做的优点有很多:
- 我们只需要做一个类似任务 2 的操作就能找到对应位的 i=2^j,具体做法就是不断使 i\leftarrow 2\times i 直到 i>\max(a,b),然后再将 i\leftarrow \frac{i}{2} 即可。
- 我们可以轻松判断这一位的异或答案,原因是此时 i\geq\min(a,b) 等价于这一位答案为 0。
- 清空 a,b 这一位的任务正好可以放在 i\leftarrow \frac{i}{2} 和 ans\leftarrow ans+i 的过程中。
找 \max/\min 的过程就是比较大小后判断是否交换两个数,于是整个流程就非常清楚了,我们得到了最初的一版异或网格。
int solve(){
int ret=0;
while(1){
if(a<b)
swap(a,b);
if(a==0)
return ret;
int i=1;
while(i<=a)
i*=2;
i/=2;
a-=i,ret+=i;
if(b>=i)
b-=i,ret-=i;
}
}
阅读下图时建议从 input 开始按照上文的思路阅读。
非常可惜,这样做的空间是 6\times 9 的,甚至比 c_2=48 还大,只能获得 40\% 的分数,所以我们得想办法压一压。
这件事情最后由出题人和验题人花了大约 2 天时间完成,中间构造出过 6\times 8 和 6\times 7 以及 6\times 6 的网格(中间的图片也许还有),最终得到了 5\times 7 的网格。
把 6\times 7 变成 6\times 6 需要重复利用其中一个变量,具体看下图的讲解。
把 6\times 6 的网格变成 5\times 7 只需要把上图蓝色部分变成任务 2 的 2^i 的做法即可。
任务 5
排序。
这个 c_1 给人一种眼前一亮的感觉,终于不再是 O(1) 的手动构造了。看样子是类似 O(10n) 的东西。
本以为这个任务的思路比较好想,结果我们可爱的验题人愣是想不出来一点,所以还是简单介绍一下。我们发现这个任务要做的是不断的比较和交换,而根据任务 4 我们已经得到了一个大小为 2\times 4 的交换器(下图当 2 中值大于 3 中值时实现了 2,3 下标中值的互换)。
所以我们大概可以猜想比较和交换节点只能有 O(n) 个。考虑到排序算法中只有 O(n) 个位置数进行比较的算法并不多(其实好像只有冒泡排序),所以我们可以锁定用冒泡排序的方法来完成此题。
考虑到我们可以循环 n 次,每次对于 i\in[1,n-1] 比较 a_i 和 a_{i+1} 的大小,并把 a_i>a_{i+1} 的两者交换,这样我们只需要把 n-1 个交换器并成一排即可。
所以我们第一版的雏形就是记录变量 i 表示当前循环的轮数,然后重复执行直到 i=n:每次比较所有相邻两数的值,若 a_x>a_{x+1} 则交换两者的值。
void solve(){
for(int i=1;i<=n;++i){
for(int j=1;j<n;++j)
if(a[j]>a[j+1])
swap(a[j],a[j+1]);
}
}
这里给出 n=4 的一种处理方法,n=50 是类似的。
精细计算发现网格大小是 16n-6 的,只能拿到 60\% 的分数。
注意到每个交换器都有清零中间变量(即上图中变量 6)的区域,而这部分区域是完全一致的,我们可以考虑将清零操作合为一个来压缩空间。
这需要一个类似而不同的思路:我们每次找到第一个 a_i>a_{i+1} 的 i。若没有就是排好序了,直接输出;否则我们交换 a_i 和 a_{i+1},并重复上述操作。
这样每次操作只需要一次交换,我们就可以在每次操作完成后清空中间变量。
void solve(){
while(1){
int fl=0;
for(int i=1;i<n;++i){
if(a[i]>a[i+1]){
swap(a[i],a[i+1]),fl=1;
break;
}
}
if(fl==0)
break;
}
}
规划一下之后发现这个东西也是好安排进网格的。下图给出 n=4 的一种实现,n=50 类似。需要注意的是,这里为了把 input 放进去把它放在了最后一个交换器的上方,这样会使得最后一个交换器的结构需要调整一下。
计算后可发现网格大小为 12n-8。
然后我们发现 n=50 的时候网格大小是 592,和 c_1 差得不多,大概还要少个 2n 才能过。
这就好办了,看到第四行全是没有用的空节点,我们考虑把 1\sim 3 行挪一半到第四行下面,这样别的节点几乎没动,而却减少了一个 n 的节点个数。
这样做空间是 \frac{21}{2}n+4 的,差一点就压进了。下图还是给出 n=4 的实现。
我们尝试把这个结构竖起来,就能压进 500 个点。下图是 n=4 的情况。
任务 6
直径。
```cpp
int get_val(int i){
if(i==1)return a[1];
if(i==2)return a[2];
if(i==3)return a[3];
...
}
```
然而我们这样判断会使得整个结构十分庞大,所以我们可以考虑另一种方式:
```cpp
int get_val(int i){
i--;if(i==0)return a[1];
i--;if(i==0)return a[2];
i--;if(i==0)return a[3];
...
}
```
转化为网格就是下图,下图支持一个从 $20$ 下标读入 $i$,并将内存条 $2i$ 中的数值复制进 $21$ 下标中。
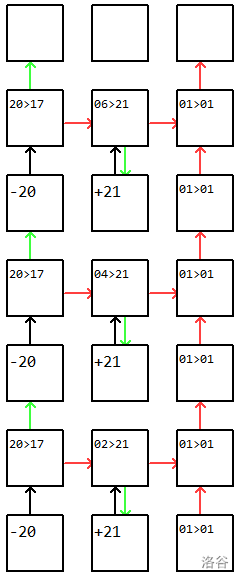
那么我们可以进入正题了:考虑树的直径怎么做。由于我们不需要保证较优的时间复杂度,我们可以考虑一些比较好做的方法。相比 `dfs`,`bfs` 的结构更容易维护,所以我们考虑构造一个类似 `bfs` 的方法来做这道题。
具体的操作比较麻烦,我们用 C++ 语言描述一下:
```cpp
int solve(){
int ans=0;
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j)
vis[j]=lst[j]=0;
int now=0;
lst[i]=1;
while(1){
now++;
ans=max(ans,now);
for(int j=1;j<n;++j){
if(lst[u[j]] || lst[v[j]])
vis[u[j]]=vis[v[j]]=1;
}
for(int j=1;j<=n;++j)
lst[j]|=vis[j],vis[j]=0;
int fl=0;
for(int j=1;j<=n;++j)
if(lst[j]==0)
fl=1;
if(fl==0)
break;
}
}
return ans;
}
```
然后我们的事情就是把代码翻译成机器人看得懂的语言,而这却是最困难的事情。
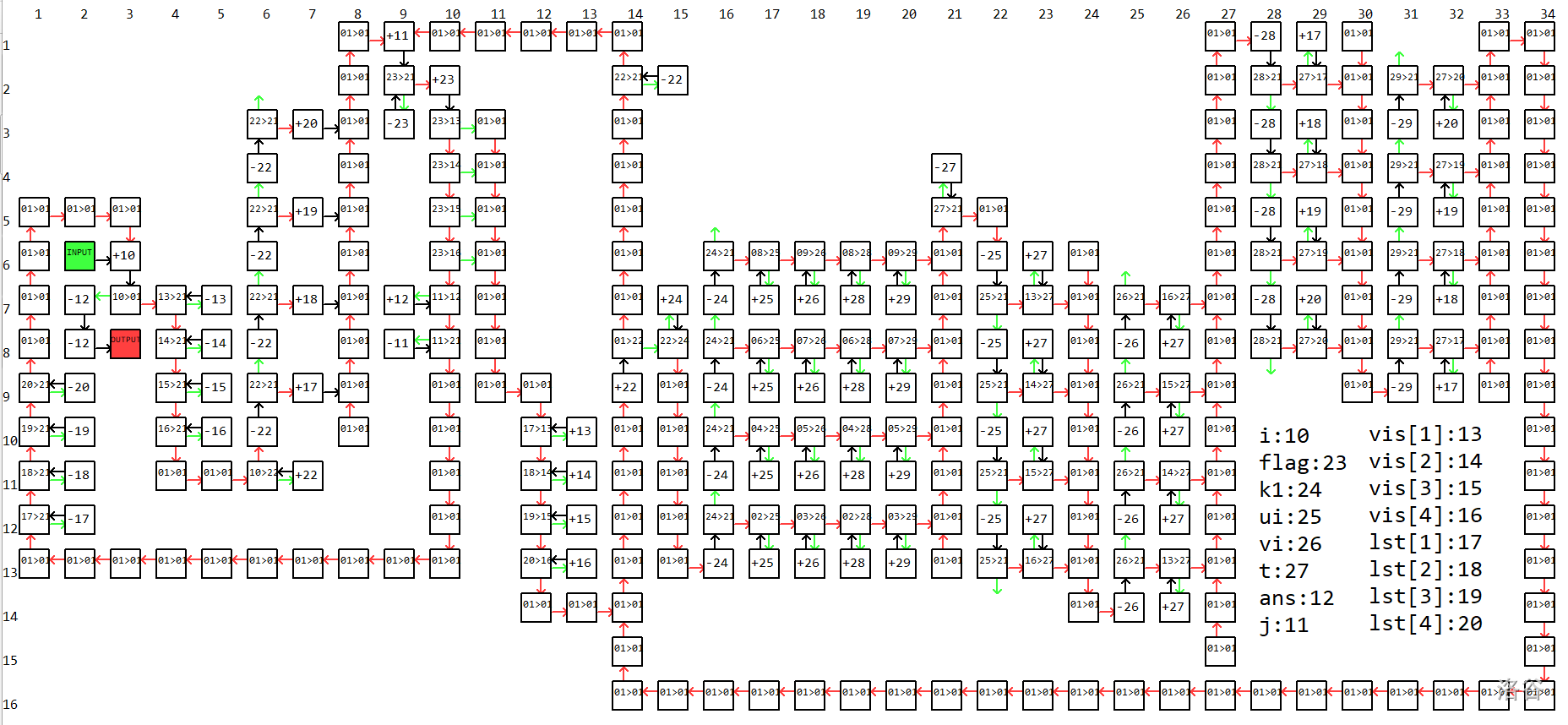
那么接下来的部分需要你自行完成,祝你好运。给个 $n=4$ 的效果图。