学习笔记——浅谈分层图
许多
·
·
算法·理论
前言
本人 APIO T1 分层图写挂爆零了,于是复习完后写下了这篇日报。
前置芝士
我们引入一道例题(模板题)来了解分层图的功能:P4822。
题目大意:给定一个图,你可以在经过一条边时让它的边权变成一半,这样的操作最多 k 次,求从 1 到 n 的最短路。
我们发现将边权变为一半这个操作非常麻烦,于是我们去看数据范围。
分层图其实非常好理解,他特别像一个三维的楼梯(个人理解)。
对于一条边,我们在每一层都连一条这样的边,**并在每一层向下一层连一条边权为一半的边**。我们一共建 $k+1$ 层,这样它最多下降 $k$ 次,对应着 $k$ 次操作。
我们口胡一个非常简单的图:
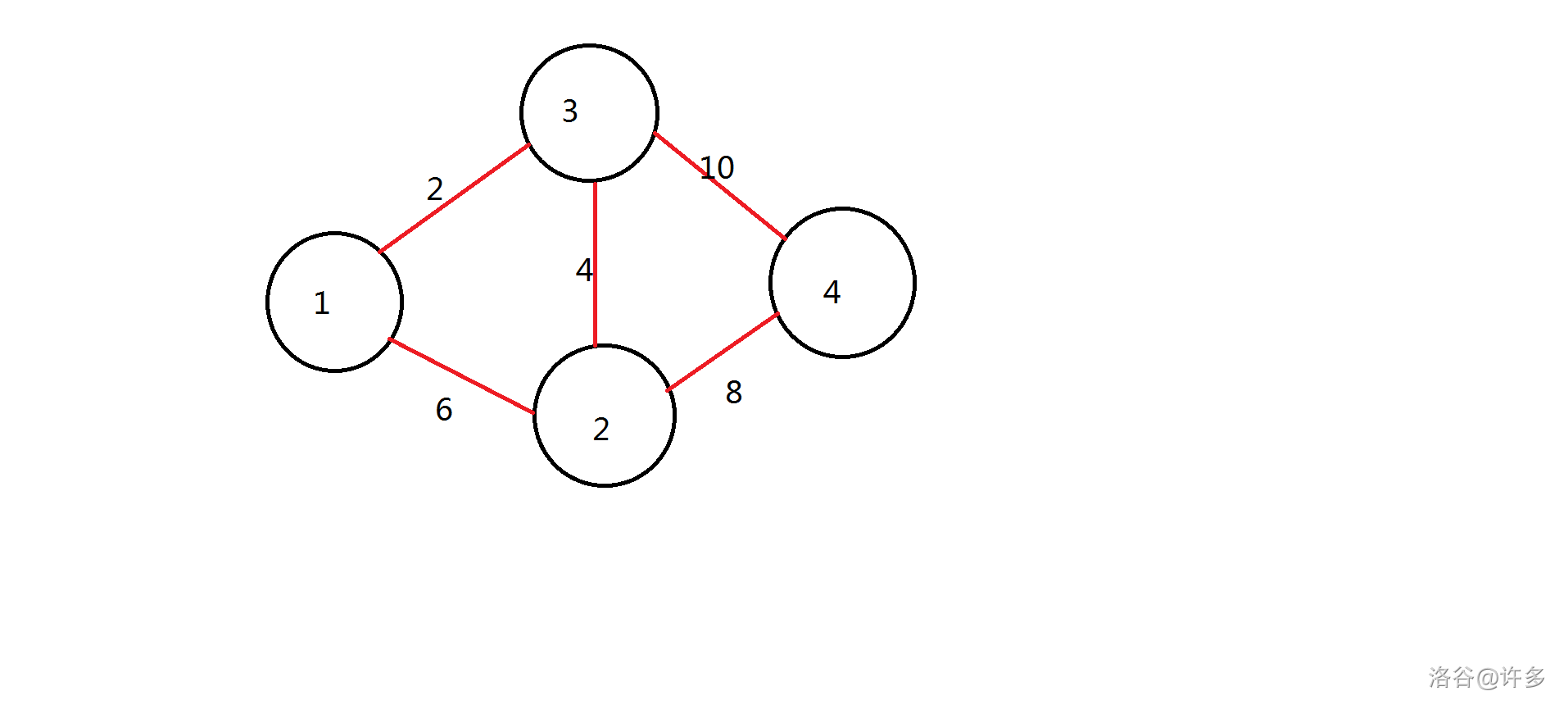
当 $k=1$ 时,图是这样的:
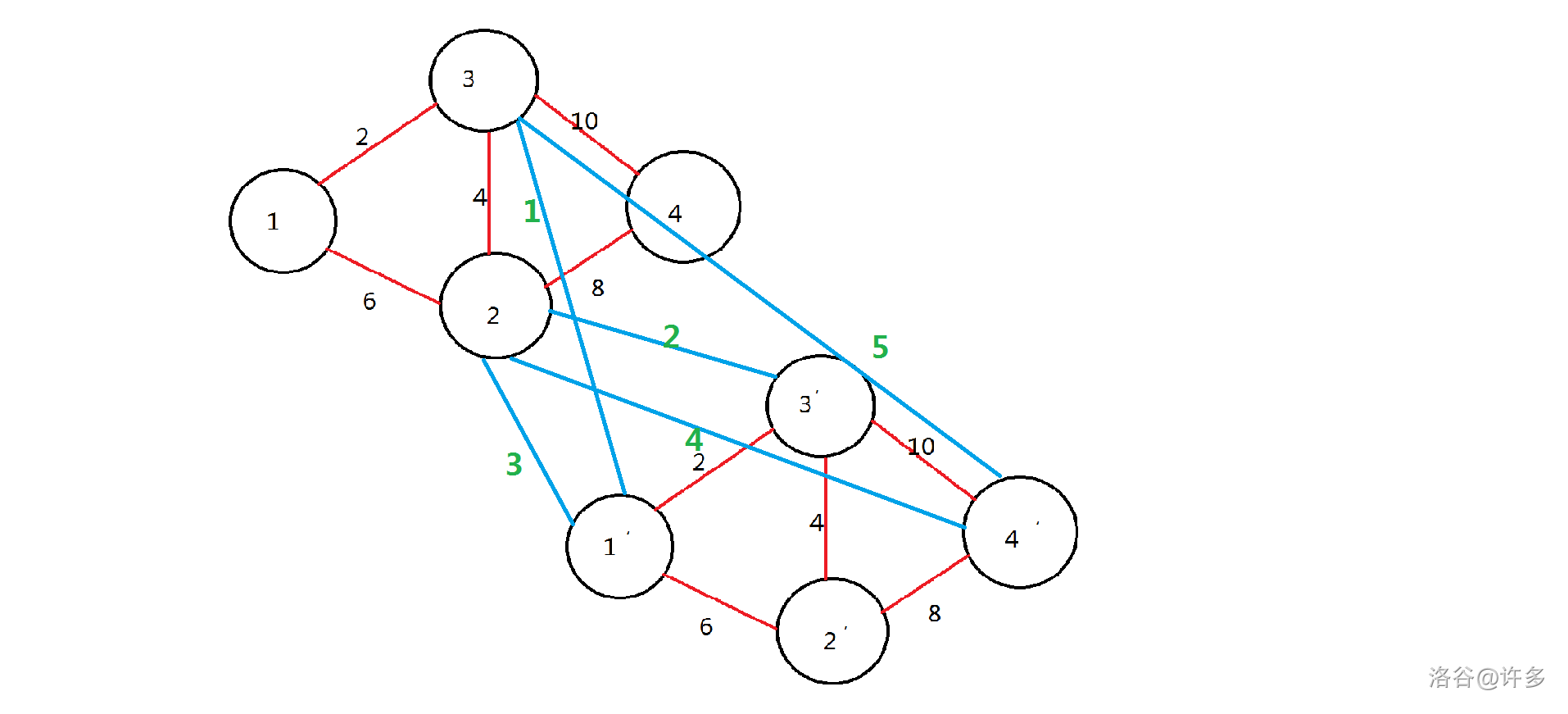
~~图画的丑,见谅~~。
然后我们在这个图上跑最短路,答案就是每一层的 $n$ 节点的最小值。
还是很难理解吗?那就放一点代码吧。
```cpp
struct node{
int to,w;
};
//建边
for(int i=1;i<=m;i++){//vector版
int u=read(),v=read(),w=read();
for(int j=0;j<k;j++){
b[u+j*n].push_back((node){v+j*n,w});b[u+j*n].push_back((node){v+(j+1)*n,w/2});
b[v+j*n].push_back((node){u+j*n,w});b[v+j*n].push_back((node){u+(j+1)*n,w/2});
}
b[u+k*n].push_back((node){v+k*n,w});
b[v+k*n].push_back((node){u+k*n,w});
}
for(int i=1;i<=m;i++){//链式前向星版
int u=read(),v=read(),w=read();
for(int j=0;j<k;j++){
add(u+j*n,v+j*n,w);add(u+j*n,v+(j+1)*n,w/2);
add(v+j*n,u+j*n,w);add(v+j*n,u+(j+1)*n,w/2);
}
add(u+k*n,v+k*n,w);
add(v+k*n,u+k*n,w);
}
//最短路跑完后的答案
int MIN=1000000000;
for(int i=0;i<=k;i++){
MIN=min(MIN,f[(i+1)*n]);
}
cout<<MIN;
//这里就不放完整代码了,分层图的核心代码说实话不多,剩下就是最短路了,这里也是相信大家都会。
```
代码中的细节还是有的,因为每层都有 $n$ 个点,所以第二层的第 $i$ 个点就是 $n+i$,第 $j$ 层的第 $i$ 个点就是 $(j+1)n+i$。
建议大家用链式前向星存边,写丑的邻接表代码真的会被卡,~~别问我怎么知道~~。
------------
相信聪明的你很快就 A 了这道题,我们来到第二题:[P4568](https://www.luogu.com.cn/problem/P4568)。
这道题虽然是蓝题,但跟上面那道并没有太大的区别,不过建图的时候注意连向下一层的边权是 $0$。
```cpp
for(int i=1;i<=m;i++){//vector版
int u=read()+1,v=read()+1,w=read();//本题点是从0到n-1
for(int j=0;j<k;j++){
b[u+j*n].push_back((node){v+j*n,w});b[u+j*n].push_back((node){v+(j+1)*n,0});
b[v+j*n].push_back((node){u+j*n,w});b[v+j*n].push_back((node){u+(j+1)*n,0});
}
b[u+k*n].push_back((node){v+k*n,w});
b[v+k*n].push_back((node){u+k*n,w});
}
for(int i=1;i<=m;i++){//链式前向星版
int u=read()+1,v=read()+1,w=read();
for(int j=0;j<k;j++){
add(u+j*n,v+j*n,w);add(u+j*n,v+(j+1)*n,0);
add(v+j*n,u+j*n,w);add(v+j*n,u+(j+1)*n,0);
}
add(u+k*n,v+k*n,w);
add(v+k*n,u+k*n,w);
}
```
### ~~[自掘坟墓 APIO2023 T1 P9370](https://www.luogu.com.cn/problem/P9370)~~
~~虽然我被薄纱了~~,但这题确实是分层图好题。
这个题有两种特殊功能,一个可以让当前总通过时间为 $0$。一个拥有让当前总通行时间除以 $2$ 的能力,除以二的能力最多用 $k$ 次。
我们先看第一个特殊能力,也就是 $arr[i]=0$,实际上就是把这个点当做起点跑最短路,但注意题目还有一个要求,就是一旦到达重点,就不能移动到其他任何地方。所以我们先跑一遍 DFS 找到所有不经过终点就能到达的点,如果终点不能到达,输出 $-1$,如果能到达,将起点和 $arr[i]=0$ 的点放入队列跑多源最短路。
我们再看第二种特殊能力,也就是 $arr[i]=2$,很显然的想法,我们对于每个与这种点连边的点,向下一层的 $i$ 连一个特殊的边,经过这条边时就将总通过时间除以二,但有一点,就是他是将**总时间**除以二,所以我们在跑 dijkstra 时应当**以层数以第一关键词,边权为第二关键词**,因为对于下一层的点,**可能到达这个点所花费的时间要低于上一层的点**,这就跟负边权类似。为了避免这种情况,我们要将层数以第一关键词,边权为第二关键词,因为上一层的最短路是相对独立的,我们可以先将上层的最短路跑完,再去跑下一层的最短路。
这题说起来比较复杂,代码上也有很多细节,建议大家在**建边的时候**终点不向其他点连边。
这题有点难度,放完整代码。
# code
```cpp
#include<bits/stdc++.h>
#include<cstdio>
//#include "cyberland.h"
#define n 100010
#define k 70
#define ar(now) arr[now-1]
using namespace std;
struct node{
int to,w,next;
}b[n*300];
int cnt=0;
struct node2{
int to;
double fnow;
};
const double inf=1e24;
int nn,hh;
bool operator<(node2 a1,node2 a2){
if((a1.to-1)/nn==(a2.to-1)/nn)return a1.fnow>a2.fnow;
return (a1.to-1)/nn>(a2.to-1)/nn;
}
bool operator>(node2 a1,node2 a2){
if((a1.to-1)/nn==(a2.to-1)/nn)return a1.fnow<a2.fnow;
return (a1.to-1)/nn<(a2.to-1)/nn;
}
double f[n*k];
int vis[n*k],head[n*k];
void add(int u,int v,int w){
b[cnt].to=v;
b[cnt].w=w;
b[cnt].next=head[u];
head[u]=cnt++;
}
priority_queue<node2>q;
inline void dfs(int now){
vis[now]=1;
if(now==hh)return ;
for(int i=head[now];i!=-1;i=b[i].next)
if(!vis[b[i].to]&&b[i].w>0)
dfs(b[i].to);
return ;
}
double solve(int N, int M, int K, int H, std::vector<int> x, std::vector<int> y, std::vector<int> c, std::vector<int> arr){
K=min(K,68);
H++;
nn=N;hh=H;
for(int i=0;i<M;i++)
x[i]++,y[i]++;
for(int i=1;i<=(N+1)*(K+1);i++)f[i]=inf,vis[i]=0,head[i]=-1;
for(int i=0;i<M;i++){
for(int j=0;j<=K;j++){
if(x[i]!=H)add(j*N+x[i],j*N+y[i],c[i]);
if(y[i]!=H)add(j*N+y[i],j*N+x[i],c[i]);
if(ar(x[i])==2&&j!=K&&y[i]!=H)
add(j*N+y[i],(j+1)*N+x[i],-c[i]);
if(ar(y[i])==2&&j!=K&&x[i]!=H)
add(j*N+x[i],(j+1)*N+y[i],-c[i]);//这里我对于向下一层的的边连负边权,表示需要/2,具体见最短路
}
}
dfs(1);
if(!vis[H])return -1;
for(int i=1;i<=N;i++){
if((vis[i]&&ar(i)==0)||i==1)
f[i]=0,q.push((node2){i,0});
vis[i]=0;
}
while(!q.empty()){
int now=q.top().to;q.pop();
if(vis[now])continue;
vis[now]=1;
for(int i=head[now];i!=-1;i=b[i].next){
double d=(b[i].w<0? (f[now]-b[i].w)*1.0/2.0:f[now]+b[i].w);
//如果边权是负的,我们就需要将总时间/2
if(d<f[b[i].to]){
f[b[i].to]=d;
if(!vis[b[i].to])q.push((node2){b[i].to,d});
}
}
}
double ans=inf;
for(int i=0;i<=K;i++)ans=min(ans,f[H+i*N]);
return ans;
}
```
闲话:邻接表被卡了,真的很慢。
[邻接表](https://www.luogu.com.cn/record/128059465)。
[链式前向星](https://www.luogu.com.cn/record/128063213)。
### 浅浅总结一下
分层图不难掌握,它将原本 $n$ 个点转成了 $n(k+1)$ 个点,在做题时一定要注意数据范围。这里还是不推荐大家用 SPFA,真的很容易被卡。
### 课后例题:
[P2939](https://www.luogu.com.cn/problem/P2939) 这题跟上面第二题没什么区别,你可以当双倍经验做,但如果真的想学习分层图,请自觉。
[P1948](https://www.luogu.com.cn/problem/P1948) 基本就是模板题。
[P3119](https://www.luogu.com.cn/problem/P3119) 这道题是分层图与其他算法的综合应用并没有太大难度。
[嘲讽作者](https://www.luogu.com.cn/problem/P9370)。