从板子到黑题的LCT
zhiyangfan
·
·
个人记录
从板子到黑题的LCT
开始前吐槽一下自己的标题,好像从紫题到黑题的跨度也不是很大(
配合题单食用:https://www.luogu.com.cn/training/157005。
本次除了题目,介绍部分也有更新。
基本算法
### 基本思路
众所周知,树链剖分的实质是重链剖分,即选择自己儿子中子树最大的一个儿子作为重儿子,然后维护重儿子链,由于重儿子的种种性质,可以保证树剖的复杂度。而 $\rm LCT$ 则依赖于一个叫做实链剖分的东西,不同于重链剖分,实链剖分的实儿子选择是较为自由的,可以随时变换儿子的虚实,当然要满足一个点只能有一个实儿子。$\rm LCT$ 的基本思路是维护这个实链剖分中的实链,以此来维护区间信息甚至树的形态信息。由于这个实儿子是我们指定的,可以随时从一条实链里删除元素加入元素改变相对关系之类的,线段树显然已经不够用,此时我们就要请出 $\rm Splay$ 这样的同样比较自由的数据结构来维护这一条条实链。
我们给每一条实链扔到一个 $\rm Splay$ 里面,显然这样会形成一个森林,我们称这个森林为辅助树。我们所有的操作是在辅助树上进行的,可以通过辅助树来还原原树的形态,但请注意 **辅助树和原树不是一个东西** ,之后有道题会专门提这一点。接下来问题来了,我们确实把实链扔进 $\rm Splay$ 里面了,以什么为权值呢?考虑到我们要通过辅助树还原原树,所以一定要存储一些形态结构的信息,所以我们以 **原树深度** 为权值,这样中序遍历一棵 $\rm Splay$ 就可以得到一个原树上从上到下的实链了。
好的,我们把实边都扔进去了,问题来了,剩下的虚边呢?如果不管的话显然原树信息就丢失了。类比重链剖分,我们能发现的是,两条实链之间的连边是虚边,所以我们考虑让虚边连接两个 $\rm Splay$ 。但问题来了,直接连接的话,虚边不就成实边了?(指成为 $\rm Splay$ 的一部分)普通的 $\rm Splay$ 的根节点对应的父亲就是空节点了,但是我们让辅助树中的 $\rm Splay$ 的每个根节点的父亲指向 **原树中** 的链的父亲结点,但不同的是,那个结点的儿子不设为根节点,即父不认子,这样既能判断根节点,也保证虚边不会在旁边看戏。接下来来看一个实例吧。
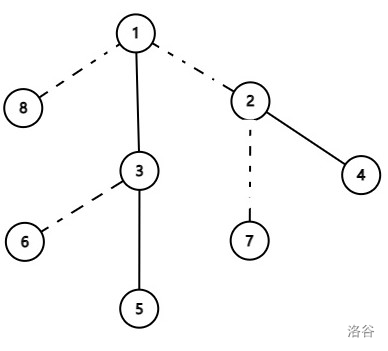
来看这棵树,其中虚线表示虚边,则我们画出来的辅助树应该长这样:
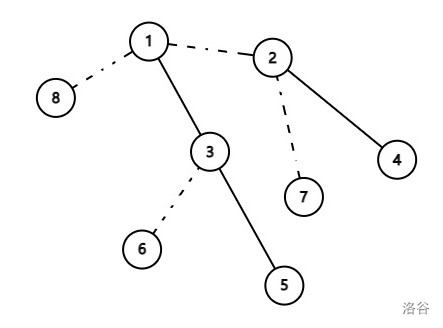
~~好像没什么区别~~ 但仔细看的话,我特意突出了实链上的左右儿子关系,其实那就是一棵以深度为权值 $\rm Splay$。然后特别地,一个点也算实链,连向原树中的父亲即可。
### 代码实现
讲了这么多干巴巴的玩意,如果不上点实际的干货确实感觉等于啥也没讲。
#### Splay 部分
$\rm Splay$ 属于前置知识了,如果不会的话,建议先去学了再来,这里只介绍一下与原版不一样的地方。最明显的是判根,一般的 $\rm Splay$ 判根可能就是看父亲节点是不是空节点。但非常遗憾,$\rm LCT$ 的辅助树上的 $\rm Splay$ 的根节点父亲结点不是空节点,而是原树上的实链父亲,不过没有关系,因为父不认子,所以我们可以写一个 `nRoot()` 函数来判一下:
```cpp
inline int nRoot(int x) { return Rs(Fa(x)) == x || Ls(Fa(x)) == x; }
```
这样就可以判断是不是根了。除此之外,因为后面的操作要求支持区间反转操作,所以我们还要给每个节点打一个 `revFlag` 标记来记录,类似文艺平衡树,然后区间反转操作就可以这样封装,然后需要的时候再下传标记即可。
```cpp
inline void reverse(int x) { swap(Ls(x), Rs(x)); node[x].revFlag ^= 1; }
```
除此之外,我们在 `splay()` 函数旋转前要先把所有的 `revFlag` 传下去,这样才能保证正确性,具体实现可以递归也可以手写栈。
```cpp
int y = st[tp = 1] = x;
while (nRoot(y)) st[++tp] = y = Fa(y);
while (tp) pushdown(st[tp--]);
```
#### access 操作
$\rm LCT$ 的核心操作,`access(x)` 的作用是打通从根节点到 `x` 的实链路径,但由于实链剖分的限制,也要把一些边变虚。因为这个函数不是很好理解,所以我打算对着代码讲解:
```cpp
inline void access(int x)
{
int y = 0;
while (x) { splay(x); Rs(x) = y; pushup(x); x = Fa(y = x); }
}
```
意外简短的代码但思想却相当复杂呢。基本思路是从下往上更新,对于节点 `x`,我们先把它旋转到当前 $\rm Splay$ 的根,令右儿子为处理的上一条实链,这样既把原来的实边改为虚边,即父不认子,又把两个实链用实边连在了一起,成为了一个更长的实链。这样不断从下往上更新就可以拉出来一条从根到 `x` 的链了。具体到代码就是 `x` 是当前处理的实链对应的 $\rm Splay$ 的根节点,而 `y` 是上一次处理实链对应的 $\rm Splay$ 的根节点。
#### makeroot
$\rm LCT$ 的又一个核心操作,`makeroot(x)` ,即把 `x` 设为它所在树的根节点。首先我们要先 `access(x); splay(x);` 。这样做之后,我们从根拉了一条到 `x` 的实链并把 `x` 转到了根。容易发现,因为 `x` 位于这条实链的最底端,所以深度一定是最大的,反映到辅助树上就是 `x` 没有右儿子。此时如果我在 `x` 上执行一个区间反转操作 `reverse(x)` ,`x` 就会没有左儿子,反映到原树上就是没有比 `x` 深度更小的结点,即 `x` 成为了原树的根。代码很简单只是调用三个函数,但却是通过修改辅助树映射原树的修改的思想的应用。
#### split
$\rm LCT$ 查询路径信息用的, `split(x, y)` 作用是把 `x` 和 `y` 之间的路径拉一条实链出来,这样我们只需要在 $\rm Splay$ 上维护一些信息就可以反映到原树的路径信息。在刚刚的操作中,唯一一个跟路径有关系的就是 `access` 操作了,所以这里的核心操作也是 `access`。考虑到 `access` 是和根节点的路径,所以我们先 `makeroot(x)` 再 `access(y)` 就可以拉出来 `x` 到 `y` 的实链了。之后为了方便操作,我们再 `splay(y)` ,之后只需要调用 `node[y]` 的相关信息就可以知道路径信息了。
#### link
$\rm LCT$ 的动态加边操作,`link(x, y)` 的作用是在 `x` 和 `y` 之间连一条边 ~~(不清楚如果连的时候不保证连完是一棵树会发生什么事)~~ 。首先我们执行一下 `makeroot(x)` 。这样的话,如果 `x` 和 `y` 之间没有边相连的话,`x` 确实是 `y` 的左儿子,但 `x` 不认 `y` 。所以我们只需要执行一下 `Fa(x) = y` 就行。
但这样需要改变树结构,常数比较大,所以还有一种已知父子关系的 `link(x, y)`,假设 `x` 是 `y` 的父亲。则我们先 `access(x); splay(x);` 把 `x` 到根的实链拉出来,然后 `splay(y)` 把 `y` 转到所在实链的根,之后连一条实边,`Rs(x) = y; Fa(y) = x;`,最后更新 `x` 的信息, `pushup(x)` 。
#### cut
$\rm LCT$ 的动态删边操作,`cut(x, y)` 的作用是删掉 `x` 和 `y` 之间的边。首先我们执行一下 `split(x, y)` 。这样的话,辅助树上 `x` 就是 `y` 的左儿子了,如果我们要完全删掉就要子不认父,父不认子,不然可能只是实变虚,即 `Fa(x) = Ls(y) = 0` 。
#### findroot
$\rm LCT$ 的找根操作,有点像并查集的 `getf(x)`,`findroot(x)` 的作用是找到 `x` 所在树的根节点。回顾刚刚的函数,和根节点有关的只有 `access(x)` 了。所以我们先拉一条 `x` 到根的路径再把 `x` 转到根方便统计,即 `access(x); splay(x);` 。之后很显然根节点就是这棵 $\rm Splay$ 中深度最小的,一直往左边跳就行,中途记得下传标记,即 `while (Ls(x)) x = Ls(x), pushdown(x);` 。最后找到的那个 `x` 就是根,不过要记得找到之后把根转到 $\rm Splay$ 的根再 `return` ,否则不能保证复杂度。
#### 完整代码
差不多就这么多函数了,接下来给出模板代码吧,这里我选的是洛谷 [P4312 [COI2009] OTOCI](https://www.luogu.com.cn/problem/P4312) 而不是板子题,因为这道题除了维护路径信息还需要维护个连通性,恰好用到了上面说过的所有函数。
```cpp
#include <cstdio>
#include <algorithm>
#define Fa(x) (node[x].fa)
#define Ls(x) (node[x].ch[0])
#define Rs(x) (node[x].ch[1])
const int N = 3e4 + 10; struct Splay{ int fa, ch[2], w, sum, revFlag; }node[N];
inline void pushup(int x) { node[x].sum = node[Ls(x)].sum + node[Rs(x)].sum + node[x].w; }
inline void reverse(int x) { std::swap(Ls(x), Rs(x)); node[x].revFlag ^= 1; }
inline void pushdown(int x)
{
if (!node[x].revFlag) return ;
if (Ls(x)) reverse(Ls(x));
if (Rs(x)) reverse(Rs(x));
node[x].revFlag = 0;
}
inline int get(int x) { return Rs(Fa(x)) == x; }
inline int nRoot(int x) { return Rs(Fa(x)) == x || Ls(Fa(x)) == x; }
inline void rotate(int x)
{
int fa = Fa(x), gf = Fa(fa), d = get(x), dd = get(fa);
//注意这里不能在最后更新,因为之后 fa 会被修改,就不能通过 nRoot(fa) 来判断 gf 是否存在了
if (nRoot(fa)) node[gf].ch[dd] = x;
node[fa].ch[d] = node[x].ch[d ^ 1]; Fa(node[x].ch[d ^ 1]) = fa;
node[x].ch[d ^ 1] = fa; Fa(fa) = x; Fa(x) = gf;
pushup(fa); pushup(x);
}
int st[N], tp;
inline void splay(int x)
{
int y = st[tp = 1] = x;
while (nRoot(y)) st[++tp] = y = Fa(y);
while (tp) pushdown(st[tp--]);
for (; nRoot(x); rotate(x)) if (nRoot(Fa(x)))
rotate(get(Fa(x)) == get(x) ? Fa(x) : x);
pushup(x);
}
inline void access(int x)
{
int y = 0;
while (x)
{
splay(x); Rs(x) = y;
pushup(x); x = Fa(y = x);
}
}
inline void makeroot(int x) { access(x); splay(x); reverse(x); }
inline void split(int x, int y) { makeroot(x); access(y); splay(y); }
inline void link(int x, int y) { makeroot(x); Fa(x) = y; }
inline void cut(int x, int y) { split(x, y); Fa(x) = Ls(y) = 0; }
inline int findRoot(int x)
{
access(x); splay(x);
while (Ls(x)) x = Ls(x), pushdown(x);
splay(x); return x;
}
int main()
{
int n, m; char s[15]; scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &node[i].w);
scanf("%d", &m); int u, v;
for (int i = 1; i <= m; ++i)
{
scanf("%s%d%d", s + 1, &u, &v);
if (s[1] == 'e')
{
if (findRoot(u) != findRoot(v)) printf("impossible\n");
else split(u, v), printf("%d\n", node[v].sum);
}
else if (s[1] == 'p') splay(u), node[u].w = v, pushup(u);
else
{
if (findRoot(u) == findRoot(v)) printf("no\n");
else printf("yes\n"), link(u, v);
}
}
return 0;
}
```
虽然代码绝对谈不上短,但都是固定的模块化的函数,理解着记忆就行了。
### 例题
像 $\rm LCT$ 这种比较死板的 DS 通常都会有一个较为灵活的应用空间,接下来我就通过几道例题介绍一下吧。因为代码比较长,所以我把所有的代码集合到一个剪切板上了:[$\tt here$](https://www.luogu.com.cn/paste/n6y4mxg6)。
#### LCT 动态维护 MST
一个比较经典的 $\rm LCT$ 应用就是动态维护最小生成树。这里的动态只指加边,删边不太行。基本思路是不断加边,当加入边 $(u,v)$ 时,如果 $u,v$ 不在一个连通块就直接 `link(u, v);` ,而如果 $u,v$ 在同一个连通块则将原来 $u,v$ 路径上的边权最大值与 $(u,v)$ 边权比较找到环上最大值,`cut` 掉即可。综合上述过程,我们需要维护的是路径边权最值的编号,应该可以用 `pushup` 操作轻易实现。需要注意的是,$\rm LCT$ 维护的是点权不是边权,所以这里需要有一个边权转点权的操作。不同于树剖那样稳定的数据结构可以用一个点代指边,$\rm LCT$ 只能在边之间加入一个新点代表边权,即 `link(x, d + n); link(d + n, y);`。其中 `d + n` 的点权为 $(u,v)$ 的边权,`u` 和 `v` 的点权是空。具体实现细节见例题代码。
##### P4172 [WC2006]水管局长
> 给出一个 $n$ 个结点 $m$ 条边的带边权无向图和 $q$ 次询问。每次询问或删掉一条边,或询问当前无向图中 $u$ 到 $v$ 的简单路径中最大边最小是多少。($1\le n\le10^3,1\le m,q\le10^5$,删掉的边不超过 $5\times10^3$ 条)
刚刚说过 $\rm LCT$ 维护 $\rm MST$ 似乎不是很支持删边,不过没有关系,这道题只有删边操作,所以显然可以改成倒序加边。之后就没什么了,唯一需要注意的是题目一开始给的是一张图,我们要先随便用啥求出来这张图的 $\rm MST$ 作为基本条件,具体细节见代码,时间复杂度 $\mathcal{O}(n\log n)$ 。
##### P2387 [NOI2014] 魔法森林
> 给出一个 $n$ 个点 $m$ 条边的无向图,每条边有两个边权 $a_i,b_i$。求出一个生成树使得 $1$ 到 $n$ 路径上的 $a_i,b_i$ 之和最小。($2\le n\le5\times10^4,0\le m\le10^5,1\le a_i,b_i\le5\times10^4$)
我们把边按照 $a_i$ 从小到大的顺序依次加入最后的生成树,这样可以保证 $a_i$ 的和最小。而这个生成树我们让它是以 $b_i$ 为权值的最小生成树,这样就可以在 $a_i$ 最小的前提下使得 $b_i$ 最小了,用 $\rm LCT$ 动态维护 $\rm MST$ 即可,时间复杂度 $\mathcal{O}(n\log n)$ 。
##### P4319 变化的道路
> 给定一棵 $n$ 个结点的树,边有边权 $w_i$,和额外的 $m$ 条边,每条边只会在第 $l$ 天到第 $r$ 天出现,求第 $1\sim d$ 天的 $\rm MST$ 上边权和。($d=32766,1\le n\le 5\times10^4,1\le w\le 10^9$)
首先我们考虑弱化版,只有额外 $m$ 条边顺次加入,那就是裸的 $\rm LCT$ 维护 $\rm MST$ 的题了。但这里加上了区间限制,而注意到加边并维护 $\rm MST$ 这个操作,只要记录了 `cut`,`link` 了哪些边,和对整体 $\rm MST$ 的影响,倒回来操作就行。而既然支持撤销,还对时间有限制,那就考虑线段树分治。时间复杂度 $\mathcal{O}(n\log^2n)$,常数巨大。
#### LCT 维护图的结构
$\rm LCT$ 除了维护图的路径信息外,图的结构也是可以动态维护的。一般来说可以维护重心,直径端点,连通块个数,割点,割边等。
##### P5385 [Cnoi2019]须臾幻境
> 给出一张无向图 $G(V,E)$,把 $E$ 中的元素排成一个长为 $|E|$ 的序列 $A$。有 $q$ 次询问,每次给出 $l,r$,询问图 $G'(V,\bigcup_{i\in[l,r]\{A_i\}})$ 的连通块个数,部分测试点强制在线。 ($1\le|V|,q\le 10^5,1\le|E|\le2\times10^5$)
首先我们考虑如果去掉区间询问这个烦人的限制该怎么做。
> 对于任意一张无向图 $G(V,E)$,如果我们找出它的生成森林 $T(V,E')$,则原图的连通块个数就为 $|V|-|E'|$。
考虑到原图有多少连通块生成森林就会有多少棵树,而每一棵树会给点和边的差贡献 $1$,这样最终的差就是树的数量,进而反映到原图的连通块个数。接下来考虑弱化版的区间:对于所有的询问,$l=1$。这样也就是询问前缀了,因为可能的前缀很少,我们可以先提前算出来,即从 $1\sim |E|$ 依次加边,每次动态维护生成森林和边的数量。问题来了,这个生成森林中出现环时该 `cut` 掉哪一条呢?显然,应该淘汰掉最早的那一条,即 $\rm LCT$ 上维护的是路径上加入时间最小边的编号。好,我们能求前缀了,接下来考虑到原题的种种限制,果断选择主席树搞一下,具体实现见代码,时间复杂度 $\mathcal{O}(n\log n)$。
##### P5489 EntropyIncreaser 与 动态图
> 给出一张 $n$ 个结点的无向图,初始时没有边。接下来有 $q$ 个操作,分为 $3$ 种,具体如下:
> 1. 在 $u,v$ 之间连一条无向边。
> 2. 求出 $u,v$ 之间的割边数。
> 3. 求出 $u,v$ 之间的割点数。
>
> 对于 2,3 操作,若 $u,v$ 不连通则输出 `-1`。($1\le n\le10^5,1\le q\le3\times10^5$)
我们把割点和割边分开看。首先考虑比较简单的,求割边。因为判连通性是非常板子的东西,这里不再阐述,我们接下来的讨论假设 $u,v$ 已连通。考虑求出 $u,v$ 所在连通块的一个生成树,则显然对于这棵树每条边都是割边,我们设权值均为 $1$,而每当尝试往这棵生成树中加入一条边 $(x,y)$ 时,$x$ 到 $y$ 会形成一个环,而这个环上的所有边显然都不是割边了,反映到树上就是 $x,y$ 路径上的所有边边权变为 $0$。最终询问时我们只需要查询 $u,v$ 路径上边的权值和即可。
接下来看割点,割点就不能像割边那样简单了。考虑一下静态求两点之间割点,有一个很套路的方法是建出原图的圆方树,则两点之间的圆点数量就是割点数。那动态就好办了,动态维护一个圆方树即可,每次出现环就建一个方点,删掉环上所有的边连向方点即可,把圆点权值设为 $1$,方点设为 $0$,查询路径权值即割点数。考虑删环这样的操作会不会对时间复杂度有破坏。考虑每次加边支付 $3\log n$ 的复杂度,则所有删环和加边操作的复杂度都被预支过了,所以最终复杂度依然是 $\mathcal{O}(n\log n)$。
##### P4271 [USACO18FEB]New Barns P
> 给定一棵树,初始时只有一个结点。接下来给出 $q$ 个操作,操作有 $2$ 种,如下:
>
> 1. 新建一个结点,并将它和一个点相连。
> 2. 查询在给定节点的连通块中与该点距离最远的点与他的距离。
>
> 保证操作合法。($1\le q\le10^5$)
首先我们能发现,一棵树上跟给定结点距离最远的结点一定是树上的直径端点。所以我们在加边的时候动态维护一下树的直径端点就好,路径长度的话我们把边权设为 $1$,路径长度就是查询的点权和 $-1$。接下来就是如何维护直径端点的问题了。当我们合并两个连通块时,得到的新直径端点一定是原来 $4$ 个点中的两个,两两求距离更新即可。存储连通块的直径端点可以考虑并查集,总之最终时间复杂度 $\mathcal{O}(n\log n)$。
##### P4115 Qtree4
## 进阶算法
啊,刚刚说到的全部都是 $\rm LCT$ 维护树链信息,但众所周知,$\rm LCT$ 有个同行树链剖分,人家维护树信息还支持维护子树信息,$\rm LCT$ 能不能呢?当然是可以的。
直观上看,$\rm LCT$ 维护子树信息好像是不太可行的,因为我们刚刚的所有操作都是基于 $\rm Splay$ 的正确维护之上的,但子树信息却不被这个所包含,注意到每个结点仅有一个实儿子是在 $\rm Splay$ 内的。但我们可以适当拓展维护的信息,考虑在维护实儿子的同时,顺便把虚儿子的信息单独维护了,这样把这俩一合并即可得到子树信息。
就以 [P4219 [BJOI2014]大融合](https://www.luogu.com.cn/problem/P4219) 这道比较板的题为例吧,这道题的要求是支持动态加边,删边和换根,并维护子树大小。则我们需要维护子树信息就是虚子树的大小,这里用 `ssiz` 表示虚子树的大小,`siz` 表示以 `x` 为根的子树大小。
```cpp
struct Splay{ int fa, ch[2], siz, ssiz, revTag; }node[N];
```
然后,`pushup` 的时候就比较简单了,就是维护一下实的信息和虚的信息:
```cpp
void pushup(int x) { node[x].siz = node[Ls(x)].siz + node[Rs(x)].siz + node[x].ssiz + 1; }
```
而注意到,这些信息只有在虚实变化的时候才会改变。考虑设两个函数 `ins(x, y), del(x, y)` 分别表示将 `y` 加入 `x` 的虚子树和移出虚子树。
```cpp
inline void ins(int x, int y) { if (!y) return ; node[x].ssiz += node[y].siz; }
inline void del(int x, int y) { if (!y) return ; node[x].ssiz -= node[y].siz; }
```
然后,这些信息要在 `access(x)` 的时候维护,毕竟要拉实链嘛。
```cpp
inline void access(int x)
{
int y = 0;
while (x) splay(x), ins(x, Rs(x)), del(x, y), Rs(x) = y, pushup(x), x = Fa(y = x);
}
```
最后询问就是直接回答 `node[x].siz`,记得先 `access(x); splay(x);` 把信息合并上来。
现在有个问题,刚刚我们的操作中用到了加法的逆运算,但如果需要维护的是类似 $\min,\max$ 这种没有逆运算的东西,那这样维护就寄了。这种情况下,我们就需要用平衡树来实现插入和维护了。
用 `std::set` 即可,时间复杂度会多一个 $\log$,而手写 $\rm Splay$ 可以不多这个 $\log$。
##### CF916E Jamie and Tree
> 给出 $n$ 个结点的有根树,你需要支持换根,子树加和查询子树和。($1\le n,q\le 10^5$)
看到换根操作可以考虑 $\rm LCT$,当然树剖也可以,真正把树剖按死的操作应该是 `link` 和 `cut`。[我的题解](https://www.luogu.com.cn/blog/i-am-zhiyangfan/solution-cf916e)。