P8994 [北大集训 2021] 经典游戏
Licykoc
·
·
题解
先考虑没有特殊能力的情况。容易发现点 u 的 SG 值为 u 到 u 子树内的最大距离,设其为 f_u。那么整个游戏的 SG 值就是 \bigoplus _u{[a_u \bmod 2=1]f_u},设其为 S。
进而得出,额外放置一枚棋子后先手仍然必胜的充要条件是 \max\{f_u\} \lt S。若不满足,则一定存在某个 f_u = S,那么只要在点 u 放置一枚棋子 S 就变成 0 了,先手必败。
于是,原问题转化为:
给定一颗树,每个点有黑白两种颜色,u 点权值 f_u 为 u 到 u 子树内的最大距离,记 S 为所有黑点权值异或和。每次操作给定 x,y,先翻转点 x 的颜色,再询问有多少个点满足:与点 y 相邻(包括点 y)且以该点为根时 \max\{f_u\} \lt S。
这里给出一种与其他两篇题解不同的维护方法。
基本思路是对每个点都维护以它为根时的 \max\{f_u\} 和 S,记为 mx_u 和 S_u。
首先一遍树形 dp 算出初始时的 mx_u 和 S_u,实现时注意 mx_u 事实上就等于 u 到 u 子树内的最大距离。
考虑修改,假设现在翻转点 u,设 mx_u 经过 (u,v) 这条边,切断 (u,v)(并不是真的切断,只是为了方便理解)。对于与 u 连通的点 x,翻转点 u 对 S_x 的贡献就是异或上 mx_u。而对于与点 v 连通的点 y,贡献则是异或上 u 到与 u 连通的点的最大距离。因为树的形态不变,所以这个可以在之前树形 dp 时预处理出来。将树以 dfs 序拍平,则上述操作可以归纳为区间异或,数据结构可以轻松维护。
再来看查询,假设查询点 u。先把 u 点父亲和点 u 暴力判掉,接下来考虑点 u 的儿子。这相当于查询:
\sum_{v\in son_u}[mx_v \lt S_v]
并不是,若对原树进行长剖,那么在修改的时候点 $v$ 要么是点 $u$ 的长儿子要么是 $u$ 点父亲,只有 $O(1)$ 种可能!这意味这点 $u$ 除去长儿子那棵子树,其他子树内的点 $x$ 应异或的值都相同,也就是那些 $P_x$ 均等于 $x$ 父亲的 $P$ 值!同理,对于 $u$ 点父亲那部分,也同样遵循上述规则。
那么查询时先暴力判断点 $u$ 的长儿子,剩余部分的查询即为:
$$\sum_{v\in son_u \setminus \{hson_u\}}[mx_v \lt S'_v \oplus P_u]$$
因为剩余部分均为轻儿子,那么 $mx_v$ 都等于 $mx_u+1$,所以查询即为:
$$\sum_{v\in son_u \setminus \{hson_u\}}[mx_u+1 \lt S'_v \oplus P_u]$$
其中 $mx_u, S'_v$ 均为不变量,$P_u$ 仅跟 $u$ 点有关,使用 trie 树轻松维护。
这就做完了?并没有,上面的分析是有漏洞的,考虑这样一张图:
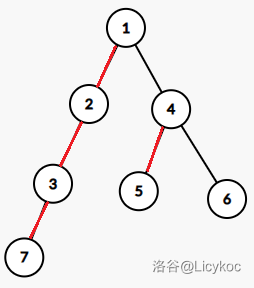
红边为重边,当前修改点 $4$,那么会切断 $(4, 1)$ 这条边,根据上面的分析,$P_4$ 应等于 $P_1$,但实际上却并不相等($P_4=4, P_1=1$)。但是这种错误只会发生在点 $4$ 这一个点上,所以我们将它暴力修改成正确的即可。
总时空复杂度:$O((n+q)\log n)$。
参考实现:
```cpp
#include <bits/stdc++.h>
constexpr int N = 2e7;
class trie {
private:
int ch[2][N], tot = 0, siz[N];
std::vector<int> root;
void modify(int &u, int x, int dep, int v) {
if (u == 0) {
u = ++tot;
}
siz[u] += v;
if (dep < 0) {
return;
}
int p = x >> dep & 1;
modify(ch[p][u], x, dep - 1, v);
}
int query(int u, int v, int x, int dep) {
if (u == 0) {
return 0;
}
if (dep < 0) {
return siz[u];
}
int pv = v >> dep & 1, px = x >> dep & 1;
return query(ch[px ^ pv][u], v, x, dep - 1) + (px == 0 ? siz[ch[pv ^ 1][u]] : 0);
}
public:
trie(int n) : root(n + 1) {}
void insert(int i, int x) {
modify(root[i], x, 30, 1);
}
void erase(int i, int x) {
modify(root[i], x, 30, -1);
}
int query(int i, int v, int x) {
return query(root[i], v, x, 30);
}
};
template<typename T>
class fenwick {
private:
int n;
std::vector<T> tr;
public:
fenwick() = default;
fenwick(int N) : n(N + 5), tr(N + 6, 0) {}
void add(int x, T y) {
++x;
for (int i = x; i <= n; i += i & -i) {
tr[i] ^= y;
}
}
void add(int l, int r, int x) {
if (l > r) {
return;
}
add(l, x);
add(r + 1, x);
}
T qry(int x) {
++x;
T res = 0;
for (int i = x; i > 0; i -= i & -i) {
res ^= tr[i];
}
return res;
}
};
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, m;
std::cin >> n >> n >> m;
std::vector<std::vector<int>> adj(n + 1);
for (int i = 1; i < n; ++i) {
int x, y;
std::cin >> x >> y;
adj[x].emplace_back(y);
adj[y].emplace_back(x);
}
std::vector<int> a(n + 1);
for (int i = 1; i <= n; ++i) {
std::cin >> a[i];
a[i] &= 1;
}
std::vector<int> max(n + 1), sec(n + 1), to(n + 1), hson(n + 1);
std::vector<int> par(n + 1), dfn(n + 1), siz(n + 1);
std::vector<int> S(n + 1);
int timer = 0;
auto dfs = [&](auto &self, int u, int fa) -> void {
if (fa > 0) {
adj[u].erase(std::find(adj[u].begin(), adj[u].end(), fa));
}
dfn[u] = ++timer;
par[u] = fa;
siz[u] = 1;
for (auto v : adj[u]) {
self(self, v, u);
if (hson[u] == 0 || max[v] > max[hson[u]]) {
hson[u] = v;
}
if (max[v] + 1 > max[u]) {
sec[u] = max[u];
max[u] = max[v] + 1;
} else {
sec[u] = std::max(sec[u], max[v] + 1);
}
siz[u] += siz[v];
}
to[u] = hson[u];
if (a[u] > 0) {
S[1] ^= max[u];
}
};
dfs(dfs, 1, 0);
auto dfs1 = [&](auto &self, int u) -> void {
for (auto v : adj[u]) {
int w = to[u] == v ? sec[u] : max[u];
if (w + 1 > max[v]) {
sec[v] = max[v];
max[v] = w + 1;
to[v] = u;
} else {
sec[v] = std::max(sec[v], w + 1);
}
w = S[u];
w ^= a[u] > 0 && to[u] == v ? max[u] ^ sec[u] : 0;
w ^= a[v] > 0 && to[v] == u ? sec[v] ^ max[v] : 0;
S[v] = w;
self(self, v);
}
};
dfs1(dfs1, 1);
trie T(n);
fenwick<int> seg(n);
auto pre = S;
for (int u = 1; u <= n; ++u) {
for (int v : adj[u]) {
if (v != hson[u]) {
T.insert(u, S[v]);
}
}
}
auto flip = [&](int u) {
auto subtree_modify = [&](int u, int v, int w) {
seg.add(dfn[u], dfn[u] + siz[u] - 1, v);
seg.add(1, dfn[u] - 1, w);
seg.add(dfn[u] + siz[u], n, w);
};
if (to[u] == par[u]) {
if (hson[par[u]] != u) {
T.erase(par[u], pre[u]);
pre[u] ^= max[u] ^ sec[u];
T.insert(par[u], pre[u]);
}
subtree_modify(u, max[u], sec[u]);
} else {
assert(to[u] == hson[u]);
subtree_modify(to[u], sec[u], max[u]);
}
a[u] ^= 1;
};
auto query = [&](int u) {
auto check = [&](int u) {
if (u < 1) {
return false;
}
return (S[u] ^ seg.qry(dfn[u])) > max[u];
};
int res = check(u) + check(hson[u]) + check(par[u]);
return res + T.query(u, seg.qry(dfn[u]), max[u] + 2);
};
while (m--) {
int x, y;
std::cin >> x >> y;
flip(x);
std::cout << query(y) << '\n';
}
}
```