学习心得 - 浅谈生成函数(GF)
ExFish
·
·
算法·理论
:::epigraph[——浅谈生成函数(GF)]
被 \mathcal O(1) 场生成函数 G 题坑惨了,必须要认真学习一下。巧合的是,422G 的前正好 200 场的 222H 也是生成函数入门。那必须致敬一下了。
:::
可能需要做的题目:ABC422G,ABC320H,ABC220H,ABC392G,P10780(P2000),P3803(P1919)。
本文参考万字长文生成函数入门。建议有小学奥数三年级初中数学基础后观看。
::::warning[食用提醒]{open}
章节不一定要按照顺序观看,因为分批写了好几次。
顺便吐槽一下洛谷的文章编辑好卡,写到 21000+ 的时候就变成 PPT 了如何呢。
注意到描述可能有问题,发现问题请及时反馈。(管理大大如果发现问题请打回并指教 awa)
::::
\tt ACL 部分介绍
::::info[\tt ACL 介绍(部分)]{open}
参考官方文件:\tt ACL/convolution。
在研究了 \tt ACL 的 \tt convolution 部分后,我解释一下如何使用相关的函数。
\tt atcoder/modint
这一部分是取模的数据类型,位于头文件 "atcoder/modint" 中,位于命名空间 atcoder:: 中。一般常用的模数函数是 atcoder::modint998244353。这个函数可以让数据自动对 998244353 取模。注意因为 __int128 只能在 64 位下运行。
\tt atcoder/convolution
这一部分是内置的卷积,位于头文件 "atcoder/convolution" 中,位于命名空间 atcoder:: 中。此文件内的函数不多,常用的是 atcoder::convolution(vector<atcoder::modint> a,vector<atcoder::modint> b)。也就是我们要计算的多项式其实要使用 vector<atcoder::modint> 存储。对应的模数可以自定义。这个函数是高效计算多项式卷积的函数,对数据有分治,在长度短的 \le 60 时会暴力。否则则会使用 NTT。(其实我没有完全看懂,但是大致是一个 NTT)
::::
前置芝士
::::info[前置芝士]{open}
多项式相关
多项式乘法:(m_1+m_2+m_3)(n_1+n_2+n_3)=m_1(n_1+n_2+n_3)+m_2(n_1+n_2+n_3)+m_3(n_1+n_2+n_3)=m_1n_1+m_2n_2+m_3n_3+m_1n_2+m_2n_3+m_3n_1+m_1n_3+m_2n_1+m_3n_2。(其实就是两两相乘啦)我们可以把这个当做多项式的卷积(感性理解一下,我看了看定义大致说的就是这个)。我们表示多项式有两种方法,分别是系数表示法和点值表示法。
系数表示法:系数相乘。求卷积复杂度 \mathcal O(n^2)。
点值表示法:也就是把 f(x) 和 g(x) 整到点上描述多项式。这样我们其实也可以用点来表示卷积的结果,于是我们可以只枚举 x,复杂度降到 \mathcal O(n)。
系数转点值:我们知道了复杂度优劣的情况,那么我们考虑转换。于是就有了四个算法:\tt DFT 朴素方法,\tt FFT 优化后的方法,\tt IDFT 转回去,\tt IFFT 同样是优化后的方法。
多项式相乘的系数:f*g 的 x^k 项系数为 \sum_{i=0}^kf_ig_{k-i}。本质就是枚举相加。
傅里叶变换 \mathcal F(x),满足 \mathcal F(g(x)f(x))=\mathcal F(g(x))\mathcal F(f(x))。
形式幂级数的导数:你说的对,形式幂级数是无限项的,但是我们一般定义形式级数为 {(\sum_{i=0}^{\infty}a_ix^i)}'=\sum_{i=\color{red} 1}^\infty{\color{red} i}a_ix^{i\color{red} -1}。
排列相关
下面 p_i 是指一个排列,长度为 n。
感性理解:置换是指 (i,p_i) 的一个一一对应的关系,我们对其建一条有向边,就可以形成若干个长度 \le n 的环,我们叫它置换环。如果你还不能理解,我这里有一张图:
阶与原根
阶:若正整数 (a,p)=1,p>1,且 p 为质数,那么我们称满足 a^n\equiv1(\bmod p) 的最小 n 我们称为 a 模 p 的阶,记作 \delta_p(a)。
原根:有正整数 n,整数 g 满足 \delta_n(g)=\varphi(n),(g,n)=1,则称 g 为 n 的一个原根。
杂项
高次展开式的系数是杨辉三角,与组合数有关。
复数的话自己看 OIwiki,作者较为懒惰。
::::
### (普通)生成函数(OGF)的定义
生成函数($\tt aka$ 母函数)是一种用**类似函数的形式**来存储信息的形式。对于一个无限序列 $a$,我们可以这样定义他的生成函数:
$$
A(x)=\sum_{i=0}^{\infty}a_ix^i
$$
你会发现这个东西有点像我们的 $x$ 进制,是一个无限的多项式,所以我们经常把这个东西叫做**多项式**。这是生成函数的一种类型,我们叫它 $\tt Ordinary \ Generating \ Function,OGF$。但是我们有无穷项,这个东西就被无聊的数学家称之为**形式幂级数**,也就是 $\tt Formal \ Power \ Series,FPS$。你说的对但是这个东西我们一般不管它具体的名字,就叫它 GF 好了。~~你没有的(扎心)~~。
然后我们有一个操作来获取这个序列的值(不然这就是个函数了),也就是 $[x^n]A(x)$,能获得 $a_n$。~~或许我们的数组访问也是这里来的。~~ 注意,这里的 $x$ 本质是一个符号,没有实际的未知数意义,你可以把它当做任意的东西。
你可能会说:这就是一个特殊的数组而已,为什么要特地研究呢?因为这个东西它竟然和组合数学有关。在组合数学中,我们通常有需要计数的东西,而这些东西可以构成**集合**,在特定的问题中,我们可以**用生成函数代替计数集合。**
### 生成函数与组合数学(案例 $1$)
假如我们有两家商店,分别售卖 $a_n=[1,2]$ 和 $b_m=[1,3]$(这里表示两个售卖物品的数组,数字为售价)的物品,问我们要买一个物品,或者在两商店各选一物品,有多少种组合方式?因此,我们有两个集合:
$$
\text{A}=\set{1_-,2_-},\text{B}=\set{1_*,3_*}
$$
当我们要买一个物品的时候,我们可以使用加法原理,也就是可以买 $\text{A}+\text{B}=\{1_-,2_-,1_*,3_*\}$ 商品。当我们需要在两个商店各选择一个物品,我们可以使用乘法原理,也就是可以买 $\text{A}\times \text{B}=\{(1_-,1_*),(1_-,3_*),(2_-,1_*),(2_-,3_*)\}$。
上面描述的是我们眼熟的乘法原理和加法原理,那么我们要尝试把它们替换成 GF ~~们~~。
$$
A(x)=\sum a_ix^i,B(x)=\sum b_jx^j
$$
对于第一种加法原理的例子,我们可以让 $c_i=a_i+b_i$,则此时 $C(x)=\sum (a_i+b_i)x_i=A(x)+B(x)$。同理,我们可以让 $d_i=a_i+b_i$,则此时 $D(x)=\sum_k(\sum_{i+j=k}a_ib_j)x^k=A(x)\times B(x)$。所以,我们成功转化了:
$$
\text{C}=\text{A}+\text{B} \Leftrightarrow C(x)=A(x)+B(x)\\
\text{D}=\text{A}\times \text{B} \Leftrightarrow D(x)=A(x)\times B(x)
$$
我们来试试展开回原式:
$$
\begin{aligned}
A(x)&=x^1+x^2 \\
B(x)&=x^1+x^3 \\
C(x)&=A(x)+B(x)\\
&= x^1+x^2+x^1+x^3 \\
&= 2x^1+x^2+x^3 \\
D(x)&=A(x)\times B(x)\\
&=(x^1+x^2)(x^1+x^3) \\
&=x^2+x^3+x^4+x^5
\end{aligned}
$$
*注:这里为了理解方便没有省略一次的显示,实际多项式不能有 $x^1$,应为 $x$。*
到这里,你就算表示了一个生成函数了。
### 生成函数与组合数学(案例 $2$)
你会说:又臭又长的式子不如我直接做,有!什!么!用!但是我们还有一个案例 ~~ABC422G(bushi)~~。
经典爬楼梯:走一步两步问走到第 $n$ 阶的方案数。你可以选择递推、矩阵快速幂,但是可以生成函数(?)。
我们定义一个爬楼梯的集合,如下:
$$
\text{Fib}=\set{\emptyset,(1),(2),(1,1),(1,2),(2,1),(2,2),(1,1,1),\dots}
$$
也就是你选择的操作序列。我们可以用一个方法来**生成**~~这才像话吗~~这个 $\text{Fib}$。
$$
\begin{aligned}
\text{Fib} &= \set{\emptyset}+\set{1}\times \set{\emptyset,(1),(2),\dots}+\set{2}\times\set{\emptyset,(1),(2),\dots} \\
&= \set{\emptyset}+\set{1}\times\text{Fib}+\set{2}\times \text{Fib}
\end{aligned}
$$
那很有趣了。接下来我们要把这坨集合改成 GF。当我们把步数改成次数,这时就出来了生成函数:
$$
\begin{aligned}
F(x)&=x^0+xF(x)+x^2F(x) \\
&=1+xF(x)+x^2F(x) \\
1&=\frac{1}{F(x)}+x+x^2 \\
\frac{1}{F(x)}&=1-x-x^2 \\
F(x)&=\frac{1}{1-x-x^2}
\end{aligned}
$$
这就是具体的生成函数。别笑,它真的**可以生成斐波那契数列**。只是我们需要[展开它的级数](https://zh.numberempire.com/taylorseriesexpansion.php)(我也不会,好像是什么 $f(x)=\sum_{i=0}^{\infty}\frac{f^{(n)}(a)\times(x-a)^n}{n!}$)就出现了:
$$
f(x)=1+x+2\,x^2+3\,x^3+5\,x^4+8\,x^5+\cdots
$$
有点意思。这样我们发现了 GF 是一个容器,只**存储必要信息但**是可以**快速且公式化计算**。在组合数学上,你可以把它理解成一个**更好用的加法、乘法原理**。
::::info[这个特殊的生成函数的拓展]
还没完!其实我们给 $1-x-x^2$ 配方,就会得到 $(1-\frac{1-\sqrt{5}}{2}x)(1-\frac{1+\sqrt{5}}{2}x)$。然后裂项,可得 $F(x)=\frac{a}{1-\frac{1-\sqrt{5}}{2}x}+\frac{b}{1-\frac{1+\sqrt{5}}{2}x}$。解出 $a,b$ 的值,就可以获得 $\text{Fib}_n=\frac{1}{\sqrt{5}}\times((\frac{1+\sqrt{5}}{2})^{n+1}-(\frac{1-\sqrt{5}}{2})^{n+1})$。
::::
### 生成函数与组合数学(案例 $3$)
*更新时间:2025 年 9 月 13 日 21 时。*
这里我将会介绍一个真正的**组合问题**,来用生成函数来做。有 $3$ 个分别有 $\set{3,2,3}$ 个,其中任意拿出 $4$ 个(有数量区别的才算不同方案)的方案数是多少。我们可以使用 $3$ 个生成函数:
$$
\begin{aligned}
A(x)&=1+x+x^2+x^3\\
B(x)&=1+x+x^2 \\
C(x)&=1+x+x^2+x^3
\end{aligned}
$$
这个问题的答案就是 $A(x)*B(x)*C(x)$ 的 $x^4$ 次项的系数。为什么呢?因为这个多项式乘法的组合意义就是选择项目。具体的,我们可以尝试展开这个多项式,我们发现 $A(x)*B(x)*C(x)=1+3x+6x^2+9x^3+10x^4+\cdots$。这里的组合意义是这样的:
|组合意义| $x^0$ 项 | $x^1$ 项 | $x^2$ 项 | $x^3$ 项 | $x^4$ 项 |
|:-:|:-:|:-:|:-:|:-:|:-:|
|意义| 不选择的方案数 | 只选择一种的方案数 | 任意选择两个的方案数 | 任意选择三个的方案数 | 任意选择四个的方案数|
|推导|三个 $0$ 次项相乘|$1\times 3$,三个组中选一个组拿一个(只会出 $3$ 个一次项)|$3\times 2\times 1$|本质是任意匹配后去重,因为多项式乘法**两两相乘**,自动会去除重复|<||
所以我们其实可以把生成函数的乘法优秀性质往组合上使用,然后就可以实现 $\binom{n}{m}$ 之类的组合了。具体的,我们**直接让组合数与生成函数建立关联**。我们有这么一个函数:
$$
f(x,n)=(x+1)^n
$$
这个函数就是最直观的生成 $\binom{n}{0},\binom{n}{1},\binom{n}{2},\binom{n}{3},\dots$ 的生成函数。这个东西的原理相信大家都懂,本质就是小学奥数的高次展开式。根据这个,我们可以推算出**广义二项式定理**。
$$
f(x,n)=\frac{1}{(x+1)^n}=\sum_{i=0}^{\infty}\operatorname{C}_{n+i-1}^{i-1}x^i
$$
### 生成函数的结构
我们发现乘法原理和加法原理远远不够用。那么我们可以考虑把他们**合起来**,这样我们就完成了一个集合向另一个集合的映射,我们叫它**生成函数的结构**。(一头雾水)
我们考虑以下案例:
$$
\text{struct}(\text{A})=\mathcal E+\text{A}+\text{A}\times \text{A}+\text{A}\times \text{A}\times \text{A}+\cdots=\sum_{i=0}^{\infty}\text{A}^i
$$
也就是由长度为任意的 $\text{A}$ 组成的集合 $\text{struct}(\text{A})$。我们把这坨东西扔到 GF 上,也就是:
$$
S(x)=1+A(x)+A(x)^2+A(x)^3+\cdots=\sum_{i=0}^{\infty}A(x)=\frac{1}{1-A(x)}
$$
~~(这个东西是用等比数列推出来的,读者自证应当不难,又是小学奥数哈)~~
我们可以用 $S(x)$ 来简化上文中 $F(x)$ 的推理过程,这时我们的 $A(x)=x+x^2$,然后我们就可以得到 $S(x)=\frac{1}{1-x-x^2}$,我们把 $S(x)$ 左侧的东西展开,就变回了次数为斐波那契数列的多项式。
但是我们发现这坨东西好像又双叒叕很没用啊!不就是把上面的斐波那契数列的展开变的稍微简单亿点而已了吗!
我们有如下的案例:你一开始在 $(0,0)$,你可以走到 $(x+a,y+b),(a,b)\neq (0,0)$,且 $0\leq a,b$ 可以自定义。求走到 $(n,n)$ 的方法数。这是一个很经典的问题,应当容易发现一个贡献的方式,然后直接组合数 $\mathcal O(n)$ 秒杀。
我们考虑对移动造一个生成函数的结构,为了表示方便,我们在这里把 $-$ 称作 $+$ 的逆运算。
$$
\begin{aligned}
\text{A}&=(\mathcal E+\text{H}+\text{H}^2+\cdots)\times(\mathcal E+\text{W}+\text{W}^2+\cdots)-\mathcal E \\
&= \text{struct}(\text{H})\times \text{struct}(\text{W})-\mathcal E
\end{aligned}
$$
然后我们发现我们需要定义一个**带有两个变量**的生成函数 $A(x,y)$ 来解决问题。因为我们可以解决 $\text{struct}(\text{H})$ 和 $\text{struct}(\text{W})$,所以 $A(x,y)=(\frac{1}{1-x})(\frac{1}{1-y})-1=\frac{1}{(x-1)(y-1)}-1$。
我们发现 $A$ 本质也需要再次解构,才能得到答案的生成函数 $F(x,y)=\frac{1}{1-A(x,y)}=\frac{(1-x)(1-y)}{1-2x-2y+2xy}$。
这一坨生成函数如何提取答案?答案就是 $F(x,y)$ 的 $x^ny^n$ 次项系数。我们来看提取结果:
$$
\begin{aligned}
[x^ay^b]\frac{1}{1-2x-2y+2xy}&=\sum_{i=0}^{\infty}(2xy-2x-2y)^i\\
&=\sum_{i=\max(a,b)}^{a+b}\binom{i}{a+b-i,i-a,i-b}2^i(-1)^{b-a}
\end{aligned}
$$
其实就是重新解构 $F$,得出一个简洁的贡献生成函数,然后转化出容斥了。
### 生成函数的多重结构
接着我们来讨论操作可以重复的情况,也就是我们的 $\text{struct}$ 升级成了 $\text{multiset}$。
我们给如下定义,$\text{B}=\text{multiset}(\text{A})$ 表示 $\text{B}$ 是 $\text{A}$ 的多重操作集。那么我们就会有如下两个生成函数:
$$
B(x)=\text{exp}(\sum_{0<k}\frac{A(x^k)}{k})
$$
这是什么?这可以对应这个组合问题:有很多个球($\ge100^{{100}^{100}}$),每一个重 $a_w$ 的球有 $a_w$ **种**(注意不是**个**),我们现在要把一些球装进一个袋子,我们要求使得总重量为 $w$ 的方案数 $b_w$。也就是说我们从单选操作变成了多选操作。
这时我们令 $B(x)=\text{exp}(\sum_{0<k}\frac{A(x^k)}{k})$,就会发现 $A(x)$ 和 $B(x)$ 是 $a_w$ 和 $b_w$ 的生成函数。我一开始读到这里我也不清楚是怎么回事,但是我们先简单化问题:令所有的球重量都为 $1$,我们需要的生成函数就是多选择函数 $H(n,r)$,里面包括 $r$ 个如下的 $\text{C}$。我们用 $\text{C}_i$ 对应每一个球的结构($\text{struct}$)也就是从 $\text{C}_i$ 中选择 $0\sim\infty$ 个球。我们把这些 $\text{C}$ 表示出来吧:
$$
\begin{aligned}
(\mathcal E+\text{C}_1+\text{C}_1^2+\text{C}_1^3+\cdots) &\times \\
(\mathcal E+\text{C}_2+\text{C}_2^2+\text{C}_2^3+\cdots)&\times \\
& \dots \\
(\mathcal E+\text{C}_r+\text{C}_r^2+\text{C}_r^3+\cdots)&\\
&=\prod_{i=1}^r\sum_{j=0}^{\infty}\text{C}^{j}_{i}
\end{aligned}
$$
我们先把 $\text{C}$ 给对应到生成函数 $C(x)$。
$$
\frac{1}{(1-C(x))^r}=\sum_{i=0}^{\infty}\binom{r+i-1}{r-1}C(x)^i
$$
(这里解构了 $C$,然后其实就已经对应上了上面的一坨多选公式)
我们令 $\text{D}_k$ 为重量为 $k$ 的球所整出的 $\text{struct}$,可以得出:
$$
\text{B}=\prod_{0<k}(\sum_{i=0}^{\infty} \text{D}_k)^{a_k}
$$
变成生成函数($x$ 代替 $D_k$):
$$
B(x)=\prod_{0<k}(\frac{1}{1-x^k})^{a_k}
$$
*接下来比较科技,因为本人不知道 $\text{exp log}$ trick 是什么,所以我直接搬运题解的科技。*
$$
\begin{aligned}
B(x)&=\text{exp} \log B(x)\\
&=\text{exp}\sum_{0<k}-a_k\log(1-x^k)\\
&=\text{exp}\sum_{0<k}a_k\sum_{0<i}\frac{x^{ik}}{i} \\
&=\text{exp}(\sum_{0<i}\frac{A(x^i)}{i})
\end{aligned}
$$
呼~ 玄幻的东西。
### (指数)生成函数(EGF)
*更新时间:2025 年 9 月 13 日 14 时。*
我们有了求组合的生成函数,那么有没有求排列的生成函数呢?有的兄弟有的。我们发现这时候的 $a_0,a_1,a_2,a_3,\dots$ 较为复杂,这时候我们考虑处理 $\frac{a_0}{0!},\frac{a_1}{1!},\frac{a_2}{2!},\frac{a_3}{3!},\dots$ 这些东西。熟悉高等数学的小朋友们 $e^x=\sum_{i=0}^{\infty}\frac{x^i}{i!}$,所以我们在使用指数型生成函数一般会用这个推导。如下可以表示一个**指数型生成函数**。
$$
\hat{A}(x)=\sum_{n=0}^{\infty}\frac{a_n}{n!}x^n
$$
同样我们有一个获取系数的操作:$[\frac{x^n}{n!}]\hat{A}(x)=a_n$。我们注意到了一个重要的性质:指数型生成函数的卷积是它的加权卷积,这个东西可以搞出排列相关的东西,如下:
$$
\begin{aligned}
[\frac{x^k}{k!}]\hat{A}(x)\hat{B}(x)&=[\frac{x^k}{k!}](\sum_{i=0}^{\infty}\frac{a_i}{i!}x^i)(\sum_{j=0}^{\infty}\frac{b_j}{j!}x^j)\\
&=k!\sum_{i+j=k}\frac{a_ib_j}{i!j!}\\
&=\sum_{i+j=k}\binom{k}{i}a_ib_j
\end{aligned}
$$
因为你发现你不过是把 $a_n$ 乘上了一个 $\frac{1}{n!}$,所以对普通生成函数通用的加法原理和乘法原理都是在这里通用的。
### 指数生成函数与排列计数
我们有这几个数字:$\set{1,1,1,6,6,8}$,问这能组成多少个四位数?显然这是一个**排列计数**问题,我们考虑使用指数生成函数解决这个问题。我们发现数字具体的值其实是无伤大雅的,于是我们考虑把取数集合转化成生成函数:
$$
\hat{F}(x)=(1+x+\frac{x^2}{2!}+\frac{x^3}{3!})(1+x+\frac{x^2}{2!})(1+x)
$$
使用一点草稿纸后我们可以**手动展开**这个函数,结果如下:
$$
\hat{F}(x)=1+3x+8\frac{x^2}{2!}+19\frac{x^3}{3!}+38\frac{x^4}{4!}+60\frac{x^5}{5!}+60\frac{x^6}{6!}
$$
这里 $x_i$ 次项系数就是构成 $i$ 位数的数字个数。这时我们的 $\frac{1}{i!}$ 就派上了把**组合**去掉的顺序**乘回去**的作用,其实就是在上面的 $\text{multiset}$ 里面的分母。这样,我们就实现了生成函数在排列上的运用。
### 指数生成函数的运用
*更新时间:2025 年 10 月 10 日 15 时。*
这里会给一些比较经典的指数型生成函数相关问题。
#### 排列问题
这个是比较经典的运用。因为长度为 $n$ 的排列一共有 $n!$ 种,所以我们有系数 $n!$。综合上面指数生成函数的式子我们可以得出 $\hat{P}(x)=\sum_{n=0}^\infty\frac{n!x^n}{n!}$,但是我们发现可以消去 $n!$ 的贡献,$\hat{P}(x)=\sum_{n=0}^\infty x^n=\frac{1}{1-x}$。你可以从这里看出指数型生成函数和普通生成函数的区别:**一个本质是 $+$,一个本质是 $\times$**。在普通生成函数里 $f(x)=\frac{1}{1-x}$ 的系数都是 $1$,而在指数生成函数里系数为 $1$ 却代表着 $n!$ 种的排列。我可能说的不够直观:也就是排列和组合之中多乘上的那个**代表顺序的 $n!$**,在这里出现了。
#### 圆排列问题
排列可以出现旋转相等了。显然我们需要除去的是一个排列的 $n$ 种旋转方式,最终公式就是一行简洁的 $(n-1)!$。对应到指数生产数就是 $\hat{Q}(x)=\sum_{n=1}^\infty\frac{(n-1)!x^n}{n!}=\sum_{n=1}^\infty\frac{x^n}{n}=-\ln(1-x)=\ln(\frac{1}{1-x})$。
那我们发现了一个事情:$\exp \hat{Q}(x)=\hat{P}(x)$。我们该如何理解多项式多一个 $\exp$ 的含义呢?长度为 $n$ 的排列的方案数是把 $1,2,\dots,n$ 的数分成若干集合,然后每一个集合都形成一个置换环的方案数。一个集合形成的置换环的方案数显然是这个集合大小的**圆排列方案数**。那么排列 $P$ 其实就是把 $1,2,\dots,n$ 的数划分为若干个圆排列 $Q$,方案数就是每一个**圆排列方案数的积**。这就是为什么会多一个 $\exp$。
我们注意到圆排列不一定要局限于一些环。我们可以把它们延伸到树上。如果一个 $n$ 个点带标号的生成树的 EGF 是 $\hat{F}(x)$,那么我们就可以得出**生成森林**的 EGF 为 $\exp \hat{F}(x)$。本质和环是一样的,把 $n$ 个点划分成若干个集合,然后就是每一个集合都是构成一个生成树的方案之积。
同理,我们还可以延伸到带标号**无向连通图**与带标号**无向图**的关联,前者是 $\hat{F}(x)$,后者则是 $\exp\hat{F}(x)=\sum_{n=0}^\infty2^{\binom{n}{2}}\frac{x^n}{n!}$。
#### 错排问题
一个长度为 $n$ 的排列满足 $p_i\neq i$ 就是一个错排,问长度为 $n$ 的排列有多少个,即求错排数。我们发现这个东西的本质就是置换环,这个置换环不能存在自环,也就是**不存在长度为 $1$ 的置换环**。我们可以列出这个东西的生成函数 $\hat{F}(x)=\sum_{n= 2}^\infty\frac{x^n}{n}=-\ln(1-x)-x$,得出答案就是 $[x^n]\exp(-\ln(1-x)-x)$。
### (狄利克雷)生成函数(DGF)
*更新时间:2025 年 10 月 10 日 16 时。*
类似于指数生成函数,这个东西也不是单纯的生成函数,如下:
$$
\tilde{F}(x)=\sum_{i=1}^\infty \frac{a_i}{i^x}
$$
看起来是不是有点像指数生成函数呢?但是它有一个特殊的性质:两个 DGF 的卷积其实就是它们所表示数列的**狄利克雷卷积**。
$$
\tilde{F}(x)\tilde{G}(x)=\sum_i\sum_j\frac{f_ig_j}{(ij)^x}=\sum_i\frac{1}{i^x}\sum_{d|i}f_dg_{\frac{i}{d}}
$$
这其实就是狄利克雷生成函数的名字由来。狄利克雷卷积和函数的积性有关,所以 DGF 最适合来研究狄利克雷卷积的相关问题。接下来将会讲解一些常见积性函数的 DGF。
### 拉格朗日反演定理(LIT)
*更新时间:2025 年 10 月 7 日 21 时。*
使用生成函数**解决树上问题**的工具。这个定理就是给你一个生成函数 $F(x)$,求满足 $G(F(x))=x$ 的系数,也就是求 $F(x)$ 的逆函数 $G(x)$ 的系数。满足 $[x]F(x)\neq 0$ 且 $[x]G(x)\neq 0$ 且 $[x^0]F(x)=[x^0]G(x)=0$ 则有:
$$
[x^n]G(x)=\frac{1}{n}[x^{n-1}](\frac{x}{F(x)})^n
$$
那么这是为什么?~~十分困难,请读者自行搜索,这里搬一下证明~~。
::::info[证明]{open}
:::success[引理]{open}
对于任何的形式幂级数 $F(x)$ 使得 $F(0)=0,F'(0)\neq 0$ 和任何整数 $k\in \mathbb{Z}$ 可以满足以下方程:
$$
[x^{-1}]F'(x)F^k(x)=[k=-1]
$$
证明:要是 $k\neq -1$,容易证明因为 $F'(x)F^k(x)=\frac{1}{x+1}{(F(x)^{k+1})}'$。否则我们就有 $F(x)=\sum a_ix^i$,那么:
$$
\frac{F'(x)}{F(x)}=x^{-1}\frac{1+2\frac{a_2}{a_1}x+\dots}{1+\frac{a_2}{a_1}x+\dots}
$$
因此 $k=-1$ 次项的系数为 $1$。
:::
根据这个引理,我们设 $F(x)$ 和 $G(x)$ 满足 $F(G(x))=x$,$F(0)=0$,$F'(0)\neq 0$。展开得:
$$
\begin{aligned}
F(G(x))&=x\\
F'(G)*G'&=1\\
\sum_i i([x^i]F(x))G^{i-1}G'&=1\\
\sum_i i([x^i]F(x))G^{i-1-n}G'&=G^{-n}\\
[x^i]\sum_ii([x^i]F(x))G^{i-1-n}G'&=[x^{-1}]G^{n-1}\\
n[x^n]F&=[x^{-1}]G^{-n}
\end{aligned}
$$
然后就可以转化为 $[x^n]G(x)=\frac{1}{n}[x^{n-1}](\frac{x}{F(x)})^n$ 了。
::::
### 拉格朗日反演定理的运用
可以用拉格朗日反演定理推出卡特兰数列的**组合数通项公式**。~~就是生成函数跑到组合数上了~~。
我们设 $C(x)$ 是卡特兰数列的生成函数,并令 $F(x)=C(x)-1$,就会有 $F(x)=x(F(x)+1)^2$,根据拉格朗日反演定理,可以得出 $G(x)=\frac{x}{(x+1)^2}$。因为 $G(F(x))=x$,所以可得:
$$
\begin{aligned}
[x^n]F(x)&=\frac{1}{n}[x^{n-1}](\frac{x}{G(x)})^n\\
&=\frac{1}{n}[x^{n-1}](x+1)^{2n}\\
&=\frac{1}{n}\binom{2n}{n-1}\\
&=\frac{1}{n+1}\binom{2n}{n}
\end{aligned}
$$
所以得出 $c_0=1$ 时 $c_n=\frac{1}{n+1}\binom{2n}{n}$。
### 普通生成函数转封闭形式 / [$\tt P10780$](https://www.luogu.com.cn/problem/P10780) 食物
*更新时间:2025 年 9 月 14 日 18 时。*
借着这个题稍微讲解一下生成函数是如何转**封闭形式**的。所谓的封闭形式,就是上面的 $f(x)=\frac{1}{1-x-x^2}$ 之类的形式。
就比如说最普通的一个生成函数 $f(x)=\sum_{i=0}^\infty (1)x_i$。我们要把它转化成封闭形式,就令 $S=1+x+x^2+x^3+x^4+\cdots$,然后 $xS$ 就等于 $x+x^2+x^3+x^4+x^5+\cdots$,可得 $(x-1)S=1$,则 $S=\frac{1}{1-x}$。转化完成,但是我们发现由于 $x^\infty$ 在许多情况下不是收敛的,这样的计算也就无法得出正确值。(跟[这个](https://www.baidu.com/s?ie=UTF-8&wd=%E4%B8%BA%E4%BB%80%E4%B9%88%E8%AF%B4%E6%89%80%E6%9C%89%E6%AD%A3%E6%95%B4%E6%95%B0%E4%B9%8B%E5%92%8C%E7%AD%89%E4%BA%8E%20-1/12)有异曲同工之妙)但是注意到我们形式幂级数不在意 $x$ 的取值,所以这是成立的。
我们可以使用类似的滚雪球方法,求出很多常见的生成函数经过转封闭后求出的值。比如说 $f(x)=\sum_{i=0}^\infty (-1)^ix^i$,可以转化成 $f(x)=\frac{1}{1+x}$。这里我会列出一个表格,来帮助理解。
|数列通项公式|生成函数的封闭形式 |对应数列 |
|:-:|:-:|:-:|
|$a_n=m$|$f(x)=\frac{m}{1-x}$|$m,m,m,m,m,\dots$|
|$a_n=(-1)^n$|$f(x)=\frac{1}{1+x}$|$1,-1,1,-1,1,\dots$|
|$a_n=2^n$|$f(x)=\frac{1}{1-2x}$|$1,2,4,8,16,\dots$|
|$a_n=a_{n-1}+a_{n-2}$|$f(x)=\frac{1}{1-x-x^2}$|$1,1,2,3,5,\dots$|
|$a_n=a_{n-1}+a_{n-3}$|$f(x)=\frac{1}{1-x-x^3}$|$1,1,1,2,3,\dots$|
|$a_n=a_{n-1}+a_{n-2}+a_{n-3}$|$f(x)=\frac{1}{1-x-x^2-x^3}$|$1,1,2,4,7\dots$|
|$a_n=[n\bmod 2=0]$|$f(x)=\frac{1}{1-x^2}$|$1,0,1,0,1,\dots$|
|$a_n=[n\ge m]$|$f(x)=\frac{x^m}{1-x}$|$0,\dots,0,1,1,\dots$|
|$a_n=n+1$|$f(x)=\frac{1}{(1-x)^2}$|$1,2,3,4,5,\dots$|
|$a_n=(n+1)(n+2)$|$f(x)=\frac{2}{(1-x)^3}$|$2,6,10,12,20,\dots$|
---
需要列出每一种食物的生成函数:
$$
\begin{aligned}
f_{承德汉堡}(x)&=\sum_{i=0}^{\infty}x^{2i}=\frac{1}{1-x^2}\\
f_{可乐}(x)&=x+1 \\
f_{鸡腿}(x)&=x^2+x+1 \\
f_{蜜桃多}(x)&=\sum_{i=0}^{\infty}x^{2i+1}=xf_{承德汉堡}(x)=\frac{x}{1-x^2} \\
f_{鸡块}(x)&=\sum_{i=0}^{\infty}x^{4i}=\frac{1}{1-x^4} \\
f_{包子}(x)&=x^3+x^2+x+1\\
f_{土豆片炒肉}(x)&=x+1 \\
f_{面包}(x)&=\sum_{i=0}^{\infty}x^{3i}=\frac{1}{1-x^3}
\end{aligned}
$$
~~这啥啊这是~~其实我们可以把这些东西乘起来,你发现非常巧啊,变成了 $f_{食物}(x)=\frac{x}{(x-1)^4}$。然后我们使用上面介绍过的**广义二项式定理**,就可以搞出 $f_{食物}(x)=\sum_{i=\color{red} 1}^\infty \frac{1}{6}i(i+1)(i+2)x^i$。最后我们要的是 $[x^n]f_{食物}(x)$,直接做。
::::success[参考程序]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll P=1e4+7,P6=1668;
ll n;
char ch;
int main(){
while(cin>>ch)
n=(n*10+char(ch-'0'))%P;
cout<<n*(n+1)%P*(n+2)%P*P6%P;
return 0;
}
```
::::
### 指数生成函数转封闭形式
*更新时间:2025 年 9 月 17 日 22 时。*
要是我们普通生成函数有的性质,那么指数型生成函数基本**都差不多有**。我在上面卖了个关子,也就是指数型生成函数其实可以转化成与 $\exp$ 相关的函数,我们有如下常用形式:
$$
\begin{aligned}
e^x&=\sum_{i=0}^{\infty}\frac{x^i}{i!} \\
e^{-x}&=\sum_{i=0}^{\infty}(-1)^i\frac{x^i}{i!}
\end{aligned}
$$
这是两个很常用的指数型生成函数,原理是**泰勒展开**,这里不研究。常用的转封闭形式的指数型生成函数其实也不多,这里给出剩余的:
$$
\begin{aligned}
\frac{e^x+e^{-x}}{2}&=\sum_{i=0}^{\infty}\frac{x^{2i}}{(2i)!} \\
\frac{e^x-e^{-x}}{2}&=\sum_{i=0}^{\infty}\frac{x^{2i+1}}{(2i+1)!} \\
e^{kx}&=\sum_{i=0}^{\infty}\frac{k^ix^i}{i!}=(\sum_{i=0}^\infty\frac{x^i}{i!})^k
\end{aligned}
$$
在推理的时候我们常常会使用这五个式子来推指数型生成函数。那么接下来就是例题时间。
同样是正整数的组成系列问题。我们有五个数字 $\set{1,3,5,7,9}$,问这些数字可以组成多少个 $n$ 位数,并且我们要让 $3,7$ 的出现次数为偶数。我们看到偶数次,立刻可以想到和 $\frac{e^x+e^{-x}}{2}$ 这个项有关。那么我们其实可以列出如下的生成函数:
$$
\hat{G}(x)=(\sum_{i=0}^\infty \frac{x^{2i}}{(2i)!})^2\times(\sum_{i=0}^\infty\frac{x^i}{i!})^3
$$
组合意义就是可以出现偶数次的两种数与可以出现任意次的三种数的排列。我们考虑按照生成函数转封闭的思路去化简这个函数。
$$
\begin{aligned}
\hat{G}(x)&=\frac{1}{4}(e^x+e^{-x})^2\times e^{3x} \\
&=\frac{1}{4}(e^{5x}+2e^{3x}+e^x) \\
&=\frac{1}{4}\sum_{i=0}^\infty (5^i+2\times 3^i+1)\frac{x^i}{i!}
\end{aligned}
$$
由于我们只要 $n$ 次项系数,所以我们可以得出通项公式 $a_n=\frac{1}{4}(5^n+2\times 3^n+1)$。
### 多项式求卷积 / DFT、FFT、IDFT、IFFT
*更新时间:2025 年 9 月 19 日 21 时 30 分。*
*想偷懒的小朋友可以下一个 `atcoder/convolution` 偷懒。*
我们喜欢使用多项式乘法解决生成函数的问题,但是我们只会使用 $\mathcal O(n^2)$ 的做法。所以我们考虑使用一种优化后的方法 FFT 和 IFFT。(注:一般**不使用** DFT 和 IDFT,比较无用)
::::warning[一些小贴士]{open}
虽然都知道 STL 很慢,但这不影响我们使用 `<complex>` 复数头文件。
::::
#### 单位根
我们有定义复数 ${\omega}^n=1$,则称 $\omega$ 为 **$n$ 次单位根**。我们根据复数的定义,通过单位圆的 $n$ 等分可以得出 $n$ 个 $\omega_n$,也就是 $n$ 次单位根的找法。我们从 $(1,0)$ 开始标号,**逆时针**给单位根标号,第 $k$ 个记作 $\omega_n^k$,易得 $(\omega_n^1)^k=\omega_n^k$,以及每一个单位根的的向量 $(\cos\frac{k}{n}2\pi,\sin\frac{k}{n}2\pi)$。我们有结论:
$$
\begin{aligned}
\omega_n^k &= \omega_{2n}^{2k} \\
\omega_n^k &= -\omega_n^{k+\frac{n}{2}} \\
\omega_n^0 &= \omega_n^k=1
\end{aligned}
$$
不理解的可以画一个**单位圆**(单位根所在圆)辅助理解。
#### DFT 离散傅里叶变换 / FFT 快速傅里叶变换
根据上文前置芝士里所说,我们其实是需要代入 $n$ 个 $x$ 来确定 $f(x)$ 转点值后的点。然后数学家傅里叶就代入了 $n$ 个单位根,出现的特殊点值表示就是 $\tt DFT$。显然我们需要优化这个算法,我们要**利用单位根的性质**。
我们设当前有一个多项式 $f(x)=\sum_{i=0}^na_ix^i$,考虑分治一下解决这个问题,设分治后得出的两个多项式分别为 $f_1(x)=\sum_{i=0}a_{2i}x^{i}$ 和 $f_2(x)=\sum_{i=0}a_{2i+1}x^{i}$。之后我们代入单位根:
$$
\begin{aligned}
f(\omega_n^k)&=f_1(\omega_n^{2k})+\omega_n^kf_2(\omega_n^{2k}) \\
&=f_1(\omega_\frac{n}{2}^k)+\omega_n^kf_2(\omega_\frac{n}{2}^k)\\
f(\omega_{n}^{k+\frac{n}{2}})&=f_1(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}f_2(\omega^{2k+n}_n)\\
&=f_1(\omega^k_{\frac{n}{2}})-\omega_{n}^kf2(\omega_n^{2k+n})
\end{aligned}
$$
我们发现 $f_1(\omega)$ 和 $f_2(\omega)$ 的值分别被求出,那么我们就可以使用 $\mathcal O(n)$ 的复杂度完成递归。这个东西叫做**蝴蝶变换**。实现时注意要在操作前面补 $0$ 以让递归更好进行,时间复杂度为 $\mathcal O(n\log n)$。
#### IDFT 离散傅里叶逆变换 / FFT 快速傅里叶逆变换
我们计算完之后,记得要转换回去才能找出卷积之后的值呀!这就是我们现在需要做的事情,也就是逆变换。我们发现 $\omega$ 在这里扮演很重要的角色。我们直接取出 $\omega$ 的倒数。设 $f(x)$ 为一个多项式,它的**离散傅里叶变换结果系数**代入 $g(x)$。取单位根 $\omega$ 的**倒数** $\omega^0_n,\omega^{-1}_n,\dots,\omega^{1-n}_n$ 代入 $g(x)$,得出的每个数 $\div n$,可以得出 $f(x)$ 的各项系数。我们发现这个恭喜的本质就是在 DFT 上再跑一遍 DFT 还原,就有了 IDFT。
而单位根的倒数就是其共轭复数。
#### 迭代 FFT
都知道递归慢的一批,所以我们可以把代入的 $\omega$ 先预先分组。然后我们发现每一个 $\omega$ 可以用二进制表示。我们倒置一下直接从最后分组结果往上使用二进制的运算合并,这样省去了递归,就实现了**迭代形式的 $\tt FFT$**。
#### 多项式乘法模板题 [P1919 【模板】高精度乘法](https://www.luogu.com.cn/problem/P1919) / [P3803 【模板】多项式乘法(FFT)](https://www.luogu.com.cn/problem/P3803)
把整数的每一位当作多项式的系数,然后用上述方法实现 $\tt FFT$ 求多项式卷积,最后输出即可,输出类似高精度。原版的多项式就是改改读入,去掉对 $10$ 取模。
::::success[参考程序]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define Complex complex<double>
#define Pi acos(-1)
string s,t;
int n,m;
const int N=2097153;
namespace FFT{
Complex a[N],b[N];
int ans[N],rev[N];
void init(int k){
int len=(1ll<<k);
for(int i=0;i<len;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));
return;
}
// 系数转点值 FFT
void fft(Complex *a,int n){
for(int i=0;i<n;i++)
if(i<rev[i])swap(a[i],a[rev[i]]);
for(int h=1;h<n;h*=2){
Complex OmegaN=exp(Complex(0,Pi/h));
for(int j=0;j<n;j+=h*2){
Complex Omega(1,0);
for(int k=j;k<j+h;k++){
Complex x=a[k];
Complex y=Omega*a[k+h];
a[k]=x+y; // 蝴蝶变换
a[k+h]=x-y;
Omega*=OmegaN;
}
}
}
return;
}
// 点值转系数 IFFT
void ifft(Complex *a,int n){
for(int i=0;i<n;i++)
if(i<rev[i])swap(a[i],a[rev[i]]);
for(int h=1;h<n;h*=2){
Complex OmegaN=exp(Complex(0,-Pi/h));
for(int j=0;j<n;j+=h*2){
Complex Omega(1,0);
for(int k=j;k<j+h;k++){
Complex x=a[k];
Complex y=Omega*a[k+h];
a[k]=x+y; // 蝴蝶变换
a[k+h]=x-y;
Omega*=OmegaN;
}
}
}
for(int i=0;i<n;i++)
a[i]/=n;
return;
}
}
using namespace FFT;
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>s>>t;
n=s.size(),m=t.size();
for(int i=0;i<n;i++)
a[i]=(double)(s[n-i-1]-'0');
for(int i=0;i<m;i++)
b[i]=(double)(t[m-i-1]-'0');
int Bin=1,Pow=2;
while((1ll<<Bin)<2*max(n,m)-1)
++Bin,
Pow=Pow<<1;
init(Bin);
fft(a,Pow);
fft(b,Pow);
for(int i=0;i<Pow;i++)
a[i]*=b[i];
ifft(a,Pow);
for(int i=0;i<Pow;i++){
ans[i]+=(int)(a[i].real()+0.5);
ans[i+1]+=ans[i]/10;
ans[i]%=10;
}
while(!ans[Pow]&&Pow>-1)
--Pow;
if(Pow==-1)
return cout<<0,0;
for(int i=Pow;i>=0;i--)
cout<<ans[i];
return 0;
}
```
::::
### 多项式求卷积 / NTT、FNTT、INTT、IFNTT
*更新时间:2025 年 10 月 10 日 9 分。*
::::warning[注意事项]{open}
> OI-wiki 原话:在不引起混淆的情形下,常用 NTT 来代指 FNTT。
我发现一般的资料一般不会对 NTT 和 FNTT、INTT 和 IFNTT 进行区分,故下文的 NTT、INTT 是指 FNTT 和 IFNTT。本文不涉及非优化版本。本文侧重于使用 FFT 的相关内容转化为 NTT,推荐先阅读上面的 FFT 相关内容后再阅读。
::::
**数论变换** NTT 就是 DFT 在数论基础上的实现,而**快速数论变换** FNTT 就是 FTT 在数论基础上的实现,用**有限域**上**单位根**取代复平面上的单位根。根据离散正交变换已经证明在复数域具有**循环卷积性质**的唯一变换是 DFT,这证明了在复数域上**没有更简单的**具有循环性质的离散正交变换,我们想要另一种方法就不能再在复数域上做文章。我们发现一般的 FFT 涉及大量的计算,就如我前面所说 `<complex>` 太牢了,所以我们一般求多项式的卷积都要对一个数进行取模,一般是 $998244353$。在这种背景下,我们需要学习 NTT。
#### 原根的性质
我们的 NTT 也像 FFT 一样使用了一些特殊性质减少运算,优化时间复杂度,而 NTT 也是。FFT 使用的是**单位(复)根**,而 NTT 要使用的是**原根**(见前置知识)。它的性质是:设 $n=2^k,k>1$,$p$ 为素数且 $n|(p-1)$,$g$ 为 $p$ 的一个原根。设 $g_n=g^{\frac{p-1}{n}}$,有:
$$
\begin{aligned}
g_n^n&=g^{n\times \frac{p-1}{n}}=g^{p-1}\\
g_n^\frac{n}{2}&=g^\frac{p-1}{2} \\
g_{an}^{ak}&=g^{\frac{ak(p-1)}{an}}=g^{\frac{k(p-1)}{n}}=g^k_n\\
g^n_n&\equiv 1(\bmod p)\\
g^\frac{n}{2}_n&\equiv-1(\bmod p)\\
(g_n^{k+\frac{n}{2}})^2=g_n^{2k+n}&\equiv g_n^{2k}(\bmod p)
\end{aligned}
$$
#### FFT 转 NTT
你结合一下单位根的性质,就会发现其实原根有单位根全部的性质。而一个是复数层面,一个是数论层面,可以互相转化。我们把所有的 $g$ 带入上面的 $\omega$ 即可。我们注意到推理 FFT 中使用了**共轭复数**,这个东西也可以转化为数论上的**乘以原根在模 $p$ 意义下的逆元**。
然后我们发现这就需要求 $p$ 的原根。怎么求这个东西呢?其实我们可以使用 $\varphi(p)=p-1$ 的性质,得出 $\delta_p(g)=\varphi(p)=p-1$,所以 $g$ 为 $p$ 的原根的充要条件就是 $g^{\frac{p-1}{p_i}}\not\equiv1(\bmod p)$ 且 $g^{p-1}\equiv1(\bmod p)$。($p_i$ 为 $p-1$ 的质因子)
因为原根不大,一般用枚举。对了对了,这里给一些常用素数的原根。
| $p$ | 唯一分解结果($p-1$ 的分解结果 $+1$) | $g$ |
|:-:|:-:|:-:|
| $167772161$ | $5\times2^{25}+1$ | $3$ |
| $469762049$ | $7\times 2^{26}+1$ | $3$ |
| $754974721$ | $3^2\times5\times 2^{24}+1$ | $11$ |
| $998244353$ | $7\times 17\times 2^{23}+1$ | $3$ |
| $1004535809$ | $479\times 2^{21}+1$ | $3$ |
#### 多项式乘法模板题 [P3803 【模板】多项式乘法(FFT)](https://www.luogu.com.cn/problem/P3803)
~~你说的对但是 ACL 就是用 NTT 写的。~~
直接做,参考代码如下:
::::success[参考程序]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
namespace NTT{
const ll N=1<<22,G=3,iG=332748118,P=998244353;
ll a[N],b[N];
int n,m,rev[N];
void init(int k){
int len=(1ll<<k);
for(int i=0;i<len;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));
return;
}
ll qp(ll a,ll b){
ll res=1;
for(;b;b>>=1,a=(a*a)%P)
if(b&1) res=(res*a)%P;
return res;
}
// 系数转点值 NTT
void ntt(ll *a,int n){
for(int i=0;i<n;i++)
if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int h=1;h<n;h*=2){
ll Gn=qp(G,(P-1)/(h<<1));
for(int j=0;j<n;j+=h*2){
ll G0=1;
for(int k=j;k<j+h;++k){
ll x=a[k];
ll y=G0*a[k+h]%P;
a[k]=(x+y)%P; // 蝴蝶变换
a[k+h]=(x-y+P)%P;
G0=G0*Gn%P;
}
}
}
}
// 点值转系数 INTT
void intt(ll *a,int n){
for(int i=0;i<n;i++)
if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int h=1;h<n;h*=2){
ll Gn=qp(iG,(P-1)/(h<<1));
for(int j=0;j<n;j+=h*2){
ll G0=1;
for(int k=j;k<j+h;++k){
ll x=a[k];
ll y=G0*a[k+h]%P;
a[k]=(x+y)%P; // 蝴蝶变换
a[k+h]=(x-y+P)%P;
G0=G0*Gn%P;
}
}
}
ll inv=qp(n,P-2);
for(int i=0;i<n;i++)
a[i]=a[i]*inv%P;
}
}
using namespace NTT;
int main(){
cin>>n>>m;
for(int i=0;i<=n;i++)
cin>>a[i];
for(int i=0;i<=m;i++)
cin>>b[i];
int Bin=max((int)ceil(log2(n+m)),1);
int Pow=(1<<Bin);
init(Bin);
ntt(a,Pow);
ntt(b,Pow);
for(int i=0;i<=Pow;i++)
a[i]=a[i]*b[i]%P;
intt(a,Pow);
for(int i=0;i<=n+m;i++)
cout<<a[i]<<" ";
return 0;
}
```
::::
::::info[彩蛋:FFT 与 NTT]{open}
彩蛋:由于 FFT 的实现和 NTT 特别像,我们来比对一下:
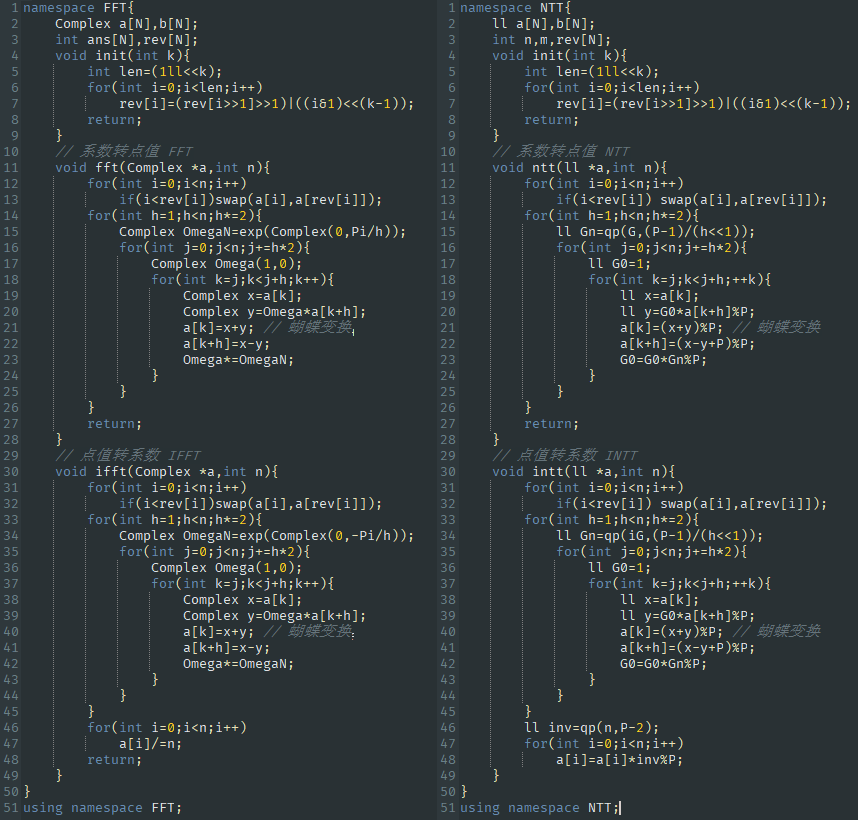
只有存储的数据类型和运算方式的部分区别,还有 $\omega$ 和 $G$ 的变量名的区别了。这可以体现出**单位根 $\omega$ 和原根 $G$ 性质基本一致。**
::::
### ABC222 [H - Beautiful Binary Tree](https://atcoder.jp/contests/abc222/tasks/abc222_h)
*更新时间:2025 年 10 月 9 日 22 时。*
求一个有 $n$ 个节点是 $1$ 的美丽树个数,具体定义可以看题面。我们发现这个东西可以列出的生成函数是 $F(x)=x(1+3F(x)+F(x)^2)^2$,根据上述公式得 $G(x)=\frac{x}{(1+3x+x^2)^2}$。
我们再反推回去,$[x^n]F(x)=\frac{1}{n}[x^{n-1}](\frac{x}{G(x)})^n=\frac{1}{n}[x^{n-1}](1+3x+x^2)^{2n}$。我们考虑对于这个式子的后半部分做文章。
$$
\begin{aligned}
T(x)&=1+3x+x^2\\
U(x)&=T(x)^m=T(x)^{2n}
\end{aligned}
$$
通过这两个关系可以得出 $U'=mT^{m-1}T'\to TU'=mT'U$。我们选择需要的是 $u_i=[x^i]U(x)$,根据上述等式得出 $u_k=\frac{3(m+1-k)u_{k-1}+(2m+2-k)u_{k-2}}{k}$。所以,我们可以从 $u_0=1$ 开始,用递归和计算逆元的方式在 $\mathcal O(n)$ 的复杂度做出这道题。
::::success[参考代码]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll p=998244353,N=1e7+10;
ll n,u[N],inv[N];
int main(){
cin>>n;
u[0]=1;
for(int i=0;i<=n;i++)
inv[i]=1;
for(int k=1;k<n;k++){
u[k]=(u[k-1]*3%p*(2*n+1-k)%p+u[k-2]*(4*n+2-k)%p)%p*inv[k]%p;
inv[k+1]=(p-inv[p%(k+1)]*(p/(k+1))%p)%p;
}
cout<<u[n-1]*inv[n]%p;
return 0;
}
```
::::
### ABC392 [G - Fine Triplets](https://atcoder.jp/contests/abc392/tasks/abc392_g)
*更新时间:2025 年 9 月 19 日 18 时。*
生成函数入门?似乎并不需要用生成函数,只是和多项式乘法相关就放在这里了。给你一个集合,求集合中满足 $B-A=C-B$ 的三元组。转换一下得 $2B=A+C$。之后我们需要计算出的是 $A+C=k$ 的二元组数量,这部分可以使用**生成函数**。
$$
f(x)=\sum_{i=0}^{n}x^{s_i}
$$
我们计算出 $f(x)^2$ 的值(注意**不是 $f^2(x)$**)组合意义就变成了任意选择两个数字相加所得出的数值,系数则是可以出现的次数。即我们要的 $2B=A+C$ 可以在 $[x^\frac{2B-1}{2}]f(x)^2$ 项上求出。这是因为我们要除去顺序与相同选择($A=C$)。代码容易得出,使用 $\tt ACL$。
::::success[参考代码($\tt ACL$)]
```cpp
#include<bits/stdc++.h>
#include<atcoder/all>
using namespace std;
#define int long long
#define cvl atcoder::convolution
const int N=1e6+10;
int n,s[N],ans;
vector<int>c;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=1e6+5;i++)
c.push_back(0);
for(int i=1;i<=n;i++)
cin>>s[i],c[s[i]]=1;
vector<int>res=cvl(c,c);
for(int i=0;i<1e6+5;i++)if(c[i])
ans+=(res[2*i]-1)/2;
cout<<ans;
return 0;
}
```
::::
### ABC422 [G - Balls and Boxes](https://atcoder.jp/contests/abc422/tasks/abc422_g)
*更新时间:2025 年 9 月 17 日 22 时。*
写这篇文章其实就是为了解决这个问题。题目就是我们要把 $n$ 个**相同 / 不相同**(两个问)的球放入三个盒子使得这三个盒子的球数分别是 $a,b,c$ 的倍数。我们可以设几个生成函数去解决这个问题。
$$
F_a(x)=\sum_{i=0}^\infty x^{ia} \\
F_b(x)=\sum_{i=0}^\infty x^{ib} \\
F_c(x)=\sum_{i=0}^\infty x^{ic}
$$
我们要求的答案就是 $[x^n]F_a(x)F_b(x)F_c(x)$。而第二问几乎一样,就是:
$$
\hat{G_a}(x)=\sum_{i=0}^\infty \frac{x^{ia}}{(ia)!} \\
\hat{G_b}(x)=\sum_{i=0}^\infty \frac{x^{ib}}{(ib)!} \\
\hat{G_c}(x)=\sum_{i=0}^\infty \frac{x^{ic}}{(ic)!}
$$
答案就是 $[\frac{x^n}{n!}]\hat{G_a}(x)\hat{G_b}(x)\hat{G_c}(x)$。这些系数可以用 `atcoder/convolution` 解决。
::::success[参考代码($\tt ACL$)]
```cpp
#include<bits/stdc++.h>
#include<atcoder/convolution>
#include<atcoder/modint>
using namespace std;
using namespace atcoder;
#define ll long long
const int N=3e5+10;
#define P modint998244353
int n,a,b,c;
P fc[N],fi[N];
int main(){
cin>>n>>a>>b>>c;
fc[0]=1;
for(int i=1;i<=n;i++) fc[i]=(fc[i-1]*i);
fi[n]=fc[n].inv();
for(int i=n;i>=1;i--) fi[i-1]=(fi[i]*i);
vector<P>f1(n+1),f2(n+1),f3(n+1);
vector<P>g1(n+1),g2(n+1),g3(n+1);
for(int i=0;i<=n;i++){
if(!(i%a))f1[i]=1;
if(!(i%b))f2[i]=1;
if(!(i%c))f3[i]=1;
}
for(int i=0;i<=n;i++){
if(!(i%a))g1[i]=fi[i];
if(!(i%b))g2[i]=fi[i];
if(!(i%c))g3[i]=fi[i];
}
auto f1f2=convolution(f1,f2);
auto f1f2f3=convolution(f1f2,f3);
auto g1g2=convolution(g1,g2);
auto g1g2g3=convolution(g1g2,g3);
cout<<f1f2f3[n].val()<<"\n"<<(g1g2g3[n]*fc[n]).val();
return 0;
}
```
::::
### 参考资料
1. [G - Balls and Boxes Editorial](https://atcoder.jp/contests/abc422/editorial/13841);
2. [H - Bullion Editorial](https://atcoder.jp/contests/abc230/editorial/3027);
3. [H - Beautiful Binary Tree Editorial]( https://atcoder.jp/contests/abc222/editorial/2765);
4. [G - Fine Triplets Editorial](https://atcoder.jp/contests/abc392/editorial/12205);
5. [算法|小学生都能看懂的生成函数入门教程](https://zhuanlan.zhihu.com/p/63003976);
6. [$\tt ACL$ 官方文件](https://atcoder.github.io/ac-library/production/document_en/convolution.html);
7. [超详细易懂FFT(快速傅里叶变换)及代码实现](https://blog.csdn.net/Flag_z/article/details/99163939);
8. [快速数论变换(NTT)超详解](https://zhuanlan.zhihu.com/p/347726949);
9. [OI wiki 多项式页面](https://oi-wiki.org/math/poly/intro/);
10. 观看的一些有关母函数 / 生成函数的书籍。
---
### 文章长度
$30000$ 字。