题解 【ARC115F Migration】

**题意** ： 给出一棵 $n$ 个节点的树，点有点权 $h_u$ 。 树上有 $k$ 块石子，记第 $i$ 块石子的位置为 $u_i$ ，则当前局面的“不稳定度”定义为 $\sum_{i=1}^kh_{u_i}$ 。 给出石子的初始位置，你的目标是将第 $i$ 个石子移动到节点 $t_i$ ，每次只能将一个石子移到相邻的节点（允许多个石子放在一个节点上），最小化过程中不稳定度的最大值。 $n\leq 2000$ ，时限$\texttt{4s}$。 ------------ 考虑二分。 记 $S$ 为初始局面，$T$ 为终止局面。 记 $H(S)$ 为局面 $S$ 的不稳定度（若不稳定度相同则比较字典序）， $f(S)$ 为局面 $S$ 所能到达（有 $mid$ 约束）的最小的 $H(V)$。 不难发现，由于操作的可逆性，$S$ 能到达 $T$ 当且仅当两者能到达的不稳定度最小的局面相同。 问题转化为求 $f(S)$ 。 ------------ 根据操作的可逆性，若 $S,S'$ 能互相到达，则 $f(S)=f(S')$ 。 那么，我们每次找出一个可达的 $S'$ 使得 $H(S')<H(S)$ ，重复若干次即可得到最小的 $H$ 。 为了便于维护，我们每次只考虑一个石子的连续移动，将这个石子（合法地）移动到一个 $H$ 更小的位置。 可以证明，若不存在这种方案，则不存在任意 $S'$ 使得 $H(S')<H(S)$。于是只用考虑这种移动就好。 显然这样的移动最多 $O(nk)$ 次。 我们需要快速求解 ： 从 $u$ 点移动，所到的点权不超过 $L$ ，能到达的最小点权。特殊地，若点权不能变小，则置为 $+\infty$ 。这个随便 dfs 预处理。 然后再用堆维护每个石子的最小出边即可。 ------------ 可以发现其实不用二分，只需每次挑一步最大不稳定度最小的转移。 记 ${\rm maxh}(u,v)$ 为路径 $(u,v)$ 的最大权值。 这样，我们对每个 $u$ 记 $t_u$ 表示 $v$ 点满足 $h_v<h_u$ 且 ${\rm maxh}(u,t_u)$ 最小（若相同，则比较 $v$ 的权值）。 当我们移动 $u$ 点时，必然会前往 $t_u$ 。 这样的复杂度为 $O(nk\log k)$ ，已经足以通过。 ------------ $t$ 的求法：考虑按 $h_u$ 从小到大加入点的过程，建立类克鲁斯卡尔重构树。然后再次从小到大考虑 $h_u$ 目标就是找到 $u$ 与更小的点的 $\rm LCA$ ，容易倍增求算。复杂度为 $O(n\log n)$。 建立一张新图，对于 $u$ ，连有向边 $u\rightarrow t_u$ ，边权为 $c_u={\rm maxh}(u,t_u)-h_u$ （即不稳定度的增量）。这形成一棵内向树。 贪心时，每次走 $c_u$ 最小的边。 - **性质** ：若 $t_a=b,t_b=c$ ，则有 $c_a\le c_b$ 。也就是说，在新树上越浅边权越大。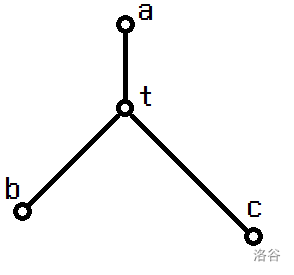 **证明** ：$a,b,c$ 的分布如下图：（其他一些情况可以视为该图的退化）  记 $A={\rm maxh}(a,t),B={\rm maxh}(b,t),C={\rm maxh}(c,t)$ 。 若 $A$ 最大或 $B$ 最大：此时 ${\rm maxh}(a,b)\geq {\rm maxh}(a,c)$ ，$t_a$ 选择 $c$ ，矛盾。 因此只可能是 $C$ 最大，则 ${\rm maxh}(a,b)=\max(A,B)\le \max(B,C)={\rm maxh}(b,c)$ . ${\rm maxh}(a,b)\le {\rm maxh}(b,c)$ 结合 $h_a\ge h_b$ 则有 $c_a\le c_b$ 。 于是，我们可以直接给边按 $c$ 从小到大排个序（也是从浅往深，若权值相同则比较深度），然后依次移动就是。 这里我们可能同时移动多个石子，用 xor Hash 维护集合特征，并记一个集合大小以计算不稳定度的变化。 可以把二分加回来以简化实现。 复杂度 $O(n\log n)$。 ```cpp #include<algorithm> #include<cstdio> #include<vector> #define ll long long #define pb push_back #define MaxN 2050 using namespace std; struct UFS{ int f[MaxN]; void Init(int n) {for (int i=1;i<=n;i++)f[i]=i;} int find(int u) {return f[u]==u ? u : f[u]=find(f[u]);} void merge(int u,int v) {f[find(u)]=find(v);} }F; int n,k,h[MaxN],p[MaxN],u1[MaxN],u2[MaxN],rnd[MaxN],o1[MaxN],o2[MaxN]; bool cmp(int A,int B){return h[A]<h[B];} vector<int> g[MaxN]; int f[12][MaxN],vist[MaxN],t[MaxN],c[MaxN],dep[MaxN]; int up(int u) { if (vist[u])return u; for (int k=10;k>=0;k--) if (!vist[f[k][u]])u=f[k][u]; return f[0][u]; } bool cmp2(int A,int B){return c[A]==c[B] ? dep[A]>dep[B] : c[A]<c[B];} const int INF=1000000000; int cnt[MaxN]; void solve(int *u,int *o,ll lim) { ll s=0; for (int i=1;i<=n;i++)o[i]=cnt[i]=0; for (int i=1;i<=k;i++){ s+=h[u[i]]; o[u[i]]^=rnd[i]; cnt[u[i]]++; } for (int i=1;i<n;i++){ int u=p[i],v=t[u]; if (!cnt[u])continue; if (s+c[u]>lim)break; o[v]^=o[u];o[u]=0; s+=1ll*cnt[u]*(h[v]-h[u]); cnt[v]+=cnt[u];cnt[u]=0; } } bool chk(ll lim) { solve(u1,o1,lim);solve(u2,o2,lim); for (int i=1;i<=n;i++)if (o1[i]!=o2[i])return 0; return 1; } int main() { scanf("%d",&n);F.Init(n); for (int i=1;i<=n;i++)scanf("%d",&h[p[i]=i]); sort(p+1,p+n+1,cmp); for (int i=1,u,v;i<n;i++){ scanf("%d%d",&u,&v); g[u].pb(v);g[v].pb(u); } for (int j=1;j<=n;j++){ int u=p[j];vist[u]=1; for (int i=0;i<g[u].size();i++){ int v=F.find(g[u][i]); if (u==v||!vist[v])continue; f[0][v]=u;F.merge(v,u); } } for (int j=1;j<=10;j++) for (int i=1;i<=n;i++) f[j][i]=f[j-1][f[j-1][i]]; for (int i=1;i<=n;i++)vist[i]=0; for (int i=1;i<=n;i++){ int u=p[i]; if (i>1){ int v=up(u); t[u]=vist[v]; c[u]=h[v]-h[u]; }else c[u]=INF; for (int v=u;!vist[v];v=f[0][v])vist[v]=u; } for (int j=2;j<=n;j++) dep[p[j]]=dep[t[p[j]]]+1; sort(p+1,p+n+1,cmp2); scanf("%d",&k); ll s1=0,s2=0; for (int i=1;i<=k;i++){ scanf("%d%d",&u1[i],&u2[i]); rnd[i]=rand()<<15^rand(); s1+=h[u1[i]];s2+=h[u2[i]]; } ll l=max(s1,s2),r=1ll<<45,mid; while(l<r){ mid=(l+r)>>1; if (chk(mid))r=mid; else l=mid+1; }printf("%lld",r); return 0; } ```