题解 AT1071 【haruki の覚醒め】
Chinshyo
2020-11-01 15:57:44
看完题面就知道是背包问题了。
# 题目分析
**题目中$ n $的数据不是特别的强,个人认为用递归的背包是更易懂的。**
求选数中大过 $ m $ 的最小的和。然而,我们就可以吧这里的和作为是背包里的物品体积。我们拿题目中样例举例:
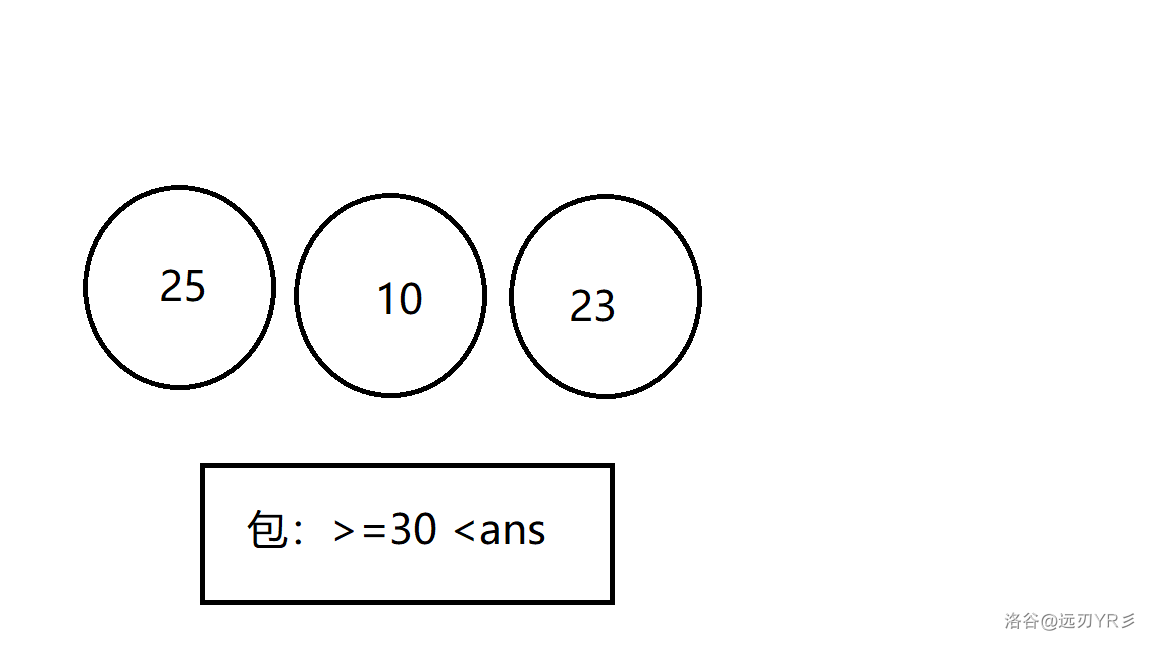
包的物品体积不得小于$ 30 $,更新时的条件比起传统的递归就要多增加这么一行语句:
```cpp
if(sum>=m)
```
这行代码就是控制背包体积不会小于 $ m $ 。
# 递归过程
我们在选数过程中用$ dep $来选举数列中的元素。分为两种情况:一种是取当前的,一种是不取当前的,所以就可以用这种代码表示:
```cpp
dfs(dep+1,sum);
if(sum+a[dep]<=ans)
dfs(dep+1,sum+a[dep]);
```
当中的剪枝条件纯粹是为了保证不$ T $的。~~其实我自己也担心递归的效率~~由于这道题没有直白的限制容积,所以不需要在这里考虑。
整个递归过程的代码:
```cpp
void dfs(int dep,int sum)
{
if(dep>n)
{
if(sum>=m)
{
if(sum<ans) ans=sum;
}
}
else
{
dfs(dep+1,sum);
if(sum+a[dep]<=ans)
dfs(dep+1,sum+a[dep]);
}
}
```
# 特殊情况
这道题有一种特殊情况,原题中:请输出最小且大于等于$ m $的,**若没有请输出$ -1 $**。所以在最后输出时要加一句:
```cpp
if(ans!=INT_MAX)
cout<<ans<<endl;
else cout<<-1<<endl;
```
# AC 代码
```cpp
#include<bits/stdc++.h>
using namespace std;
int a[55],n,m,ans=INT_MAX;
void dfs(int dep,int sum)
{
if(dep>n)
{
if(sum>=m)
{
if(sum<ans) ans=sum;
}
}
else
{
dfs(dep+1,sum);
if(sum+a[dep]<=ans)
dfs(dep+1,sum+a[dep]);
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
dfs(1,0);
if(ans!=INT_MAX)
cout<<ans<<endl;
else cout<<-1<<endl;
return 0;
}
```