Parenthesis Checking
2huk
·
·
题解
Parenthesis Checking
Description
给出一个长度为 n 的括号串,q 次以下两种操作:
- 输入 1\ l\ r,代表交换第 l 和第 r 个位置上的字符;
- 输入 2\ l\ r,判断区间 [l,r] 子串是否是合法括号序列。
## Solution
一个括号序列是合法的有这样一个 trick:
- 总共的左括号和右括号数量相等;
- 任意前缀的左括号数量 $\ge$ 右括号数量。
若将序列中左括号看作 $1$,右括号看作 $-1$,则两个条件变成了:
- 总和为 $0$;
- 任意前缀和 $\ge 0$。
---
那么考虑仅有 $2$ 操作的这个问题。每次判断某个区间是否合法也就是看这个区间的每个前缀和是否合法。具体的,若我们将上述求得的括号序列前缀和定义为 $\{s_i\}$,则需要满足:
- $s_r - s_{l - 1} = 0$ 也就是 $s_r = s_{l - 1}$;
- 任意 $k \in [l, r]$,都有 $s_k -s_{l - 1} \ge 0$ 也就是 $s_k \ge s_{l - 1}$。
对于第二个条件,我们可以将其转化为 $\min_{i = l}^r (s_i) \ge s_{l = 1}$。因为只要最小值比它大那么所有值就都比它大了。
因此若这个问题不带修,这样就已经可以了。首先求出括号序列的前缀和,并用数据结构(比如 ST 表)维护这个前缀和数组上的区间最小值,然后根据这两个条件判断即可。
---
若带修,我们可以用线段树维护。用线段树维护**括号序列前缀和数组**的值,额外维护一个区间最小值,那么在每次交换两个位置时分类:
- 若原来 $l$ 和 $r$ 位置上的元素(指原始括号序列)相同,则不做处理;
- 否则,若原来 $l$ 上为左括号,$r$ 上为右括号,则在前缀和数组上应该是 $[l, n]$ 这一段整体减 $2$,$[r, n]$ 这一段整体加 $2$,然后在原序列上交换;
- 再否则,若原来 $l$ 上为右括号,$r$ 上为左括号,则在前缀和数组上应该是 $[l, n]$ 这一段整体加 $2$,$[r, n]$ 这一段整体减 $2$,然后在原序列上交换。
例如,若要将 $4, 5$ 位置上的括号交换:
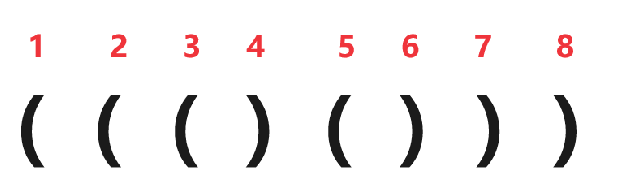
那么很显然的 $4$ 位置上原来的值 $-1 \to 1$ 也就是多了 $2$,$5$ 位置上原来的值 $1 \to -1$ 也就是少了 $2$。而一个值的变化会影响前缀和数组上当前位置以后的所有位置:
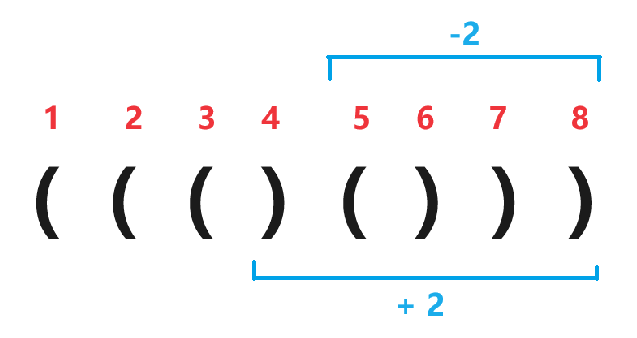
然后修改就完成了。
---
在实现上,你需要维护一颗支持区间加,单点查询,区间求最小值的线段树。其中的单点查询可以偷懒成长度为 $1$ 的区间最小值。
还需要注意,在判断当前区间是否合法时,第一个条件用到了 $l - 1$ 位置上的值,此时若 $l = 1$ 则会访问不到。因此需要特判若 $l = 1$ 时 $s_{l - 1} = 0$。否则你会挂在 case\_28 上。
## Code
[这里](https://atcoder.jp/contests/abc223/submissions/46483754)。