前言

势能分析法，是时间复杂度分析中用来分析摊还时间复杂度的一种方法。摊还时间复杂度，即将用时长的操作均摊到用时短的操作上面。如果一个数据结构它有一些操作的用时很长，但是有一些操作的用时很短，就可以使用均摊时间复杂度来描述它的时间复杂度。我们认为，用时长的操作所花的时间可以均摊到用时短的操作所花的时间上面。

引入-单调队列

前置知识：单调队列（可以在题解处学习）

在单调队列里面，包含很多入队操作和一些出队操作。时间复杂度为 \Theta(n) 的标准解释是一个元素最多入队和出队一次，这个解释很清晰，但是本文讲的是势能分析法不是神仙分析法，所以下面将用势能分析来分析其时间复杂度，同时作为引入。

令势能函数 \Phi(S)=\text{S中元素个数}。其中 S 代指单调队列的整个数据结构。对于任意单调队列，我们都可以计算出它的势能函数对应的值。例如，有三个元素为 1 3 5 的单调队列 S_1，其势能函数 \Phi(S_1)=3。

以下假设将单调队列的 push 拆分为弹出（即那个 while 循环）和 入队（弹出后的入队）。

容易得知：

• 空单调队列的势能函数为 0（即在算法开始时，势能函数为 0）
• 每次执行一个入队操作，单调队列的势能函数增加1。
• 执行弹出的时候，弹出多少个元素，势能函数就减少多少。
• 算法结束时，势能函数非负

所以我们就可以将弹出操作弹出元素时 head-- 和一次判断的开销摊到入队操作上。因为每次弹出一个元素，势能函数就会 -1。而在入队操作的时候，势能函数 +1。

有一篇英语阅读（完形填空），讲的是一个咖啡馆的故事。一些顾客买咖啡，会额外买一杯咖啡 for wall ，然后服务员会贴一张纸条到墙上。当一个衣衫褴褛的流浪汉买咖啡时，他可以买一杯咖啡 from wall ，服务员就会从墙上揭下一张纸条，然后提供给流浪汉一杯免费咖啡。势能函数就可以理解成这个故事里的 wall 。实际花费是顾客或流浪汉实际得到的咖啡，而均摊后的花费是顾客或流浪汉为这杯咖啡所付的钱。

由于每次 while 的开销都会使墙上的订单减少 1，而单次入队操作只会使墙上的订单增加 1，所以我们可以认为每次弹出和入队所花的钱都是一个常量。用势能分析的语言说，while 的开销可以由势能支付。由于柜台一分钱都没有亏，所以我们卖出的咖啡喝收到的钱一样多，所以每次弹出和入队所花的时间就可以认为是一个常量。

因此，每次弹出和入队的时间复杂度都是 \Theta(1)，出队的时间复杂度显然也是 \Theta(1)，则总时间复杂度是 \Theta(n)。

这里单调队列的算法时间有一个 for 套一个 while，虽然表面上是双重循环 \Theta(n^2) 的，但是最终却可以证明是 \Theta(n) 卡不掉的时间复杂度。这就是摊还时间复杂度的魅力。

引入-并查集乱搞也能AC

例题：P1840 Color the Axis，本节将证明一个看似乱搞算法的时间复杂度是 \Theta((n+m)\alpha(n)) 的。

附题面简述

有一个长度为 n 的序列，开始全 1，有 m 个操作，每次将一个区间赋为 0，求每次操作后 1 的数量。

这题标准解法应该是线段树区间赋值+查询，能够达到 \Theta(m\log n) 的时间复杂度。

但是线段树的题怎么能用线段树做呢。我当即拍了一个暴力解，每次循环赋 0。这个算法稳 \Theta(nm)，肯定炸。所以我就用并查集维护一些已经赋为 0 的段，并查集的代表元素选为段的最末尾一个元素，每次直接 getfa(l) 跳到段尾，然后合并来表示赋 0。

（参见题解里面某位 dalao 的解法，我这个菜鸡竟然和 dalao 想到一块了）

然后就 458ms AC。

我：？？？这不是 \Theta(nm) 加优化吗？？？

然后我想了一会，口糊出了一个时间复杂度为 \Theta((n+m)\alpha(n)) 的证明。

首先，定义一个势能函数 \Phi(S)=\text{S中不同的集合的个数}\times\alpha(n)。S表示维护这个区间的并查集。

算法开始时，并查集有 n 个不同的集合，所以算法开始时的势能函数 \Phi(S)=n\alpha(n) 。

而每次操作的时候，每次 while 循环中要执行两个步骤：

1. l=getfa(l);
2. merge(l,l+1);

这两个步骤中的步骤 2 会使势能函数减少 \alpha(n) ，刚好弥补第一个操作 \Theta(\alpha(n)) 的开销。所以，我们可以认为每次操作的 while 循环内部的耗时由势能支付。

所以，每次操作只需要负担最开始的 l=getfa(l) 的 \Theta(\alpha(n)) 的开销。由于一开始势能函数为 \Theta(n\alpha(n))，最终时间复杂度即为 \Theta((n+m)\alpha(n))。

在实际做题的时候，可以忽略 \alpha(n)，而认为其时间复杂度就是 \Theta(n+m)。

应用-Splay

前置知识：Splay

学习完 Splay，许多人都会有一个疑惑：为啥这么旋就能让均摊时间复杂度变成 \Theta(n\log n)。毕竟，旋转操作好像并没有把树平衡多少。

这里就要证明 Splay 访问一个节点并将其调整到根的开销为 \Theta(\log n)。

对于一个节点 t，定义势能函数 \Phi(t)=\log \text{siz[t]}，其中 \text{siz[t]} 表示以 t 为子树的 Splay 的大小。对于一个 Splay（命名为 S)，定义其势能函数为 \Phi(S)=\sum\limits_{x\in S}\Phi(x)。很显然，对于任意 n 次插入操作，最终势能 \Phi(t_n) 减去初始势能 \Phi(t_0) 是 \Theta(n\log n) 级别的，即用于升高势能的总花费是 \Theta(n\log n) 的，则只需要证明旋转操作所需的时间为 \Theta(\log n) 就好。

这里需要分类讨论。

1. 单旋

（图源网络，侵权删）

这里，我们定义旋转前 p 为 x 的父亲，旋转的时候旋转 x，即与左图中相应字符标注的节点所处的位置对应。旋转后 p 节点旋转成 p'，x 节点旋转成 x'，即与右图中相应字符标注的节点的位置对应。不失一般性的，我们认为左边是旋转前，右边是旋转后。

容易看出，因为这个旋转并没有影响到 A、B 和 C子树里的所有点的权值，\Delta\Phi(S) = \Phi(x')+\Phi(p')-\Phi(x)-\Phi(p)（注意，等式右边为整个 Splay 的势能，右边为单点势能）。由于 \Phi(x')=\Phi(p)（它们的大小相等），因此 \Delta\Phi(S) = \Phi(x')-\Phi(p)+\Phi(p')-\Phi(x)=\Phi(p')-\Phi(x)<\Phi(x')-\Phi(x)。

所以，本次操作经势能函数均摊后的操作时间为：

\Theta(1)+\Delta\Phi(S)<\Theta(1)+(\Phi(x')-\Phi(x))

2. 一字型旋转

除了 p、x、p'、x' 以外，再定义一个 g 和 g'，g 是 p 旋转前的父节点，g 在旋转操作过后旋转成 g'，即与图中相应字符标注的节点所处位置对应。我们仍旧认为左边是旋转前，右边是旋转后。

一步步分析。这里 \Delta\Phi(S)=\Phi(x')+\Phi(p')+\Phi(g')-\Phi(x)-\Phi(p)-\Phi(g)。

由于 \Phi(x')=\Phi(g)，可得 \Delta\Phi(S)=\Phi(p')+\Phi(g')-\Phi(x)-\Phi(p)

单旋的变化结果（\Theta(1)+(\Phi(x')-\Phi(x))）启示我们可以将单次操作后的调整后时间写成差分的形式，这样子项就会两两相抵，并且最好不要有常数项。由于 \text{siz[p]}>\text{siz[x]}，\text{siz[x']}>\text{siz[p']}，所以上式可以写成 \Delta\Phi(S)=\Phi(p')+\Phi(g')-\Phi(x)-\Phi(p)<\Phi(x')+\Phi(g')-2\Phi(x)，这就启示我们寻找 \Phi(x)+\Phi(g')-2\Phi(x')的性质。这样，只要相减，不需要的项就会自动抵消。

展开，得该式即为 \log\text{siz[x]}+\log\text{siz[g']}-2\log\text{siz[x']}。由于k\log a=\log a^k，\log a-\log b = \log \frac{a}{b}，\log a +\log b=\log (ab)，该式可以变化成：

\log(\frac{\text{siz[x]}\text{siz[g']}}{\text{siz[x']}^2})

设\text{siz[x]}=a，\text{siz[g']}=b，\text{siz[x']}=c。上式写作：

\log(\frac{ab}{c^2})

由于 \text{siz[x']}>\text{siz[x]}+\text{siz[g']}（从图中可以看出来，x'是整棵树，x包含A、B分支，g'包含C、D分支），所以 c>a+b

由于对数函数单调递增（函数值随x的增大而增大），所以可以得到：

\log(\frac{ab}{c^2})<\log(\frac{ab}{(a+b)^2})=\log(\frac{ab}{a^2+2ab+b^2})<\log(\frac{ab}{2ab})=\log(\frac{1}{2})=-1

所以：

\Phi(x)+\Phi(g')-2\Phi(x')<-1

我们又有 \Delta\Phi(S)<\Phi(x')+\Phi(g')-2\Phi(x)，所以，被势能函数均摊后的操作用时为：

\Theta(1)+\Delta\Phi(S)<\Theta(1)+\Phi(x')+\Phi(g')-2\Phi(x)-1-(\Phi(x)+\Phi(g')-2\Phi(x'))

整理一下，可以得到：

\Theta(1)+\Delta\Phi(S)<\Theta(1)-1+3\Phi(x')-3\Phi(x)

这里的 1 可以将 \Theta(1) 均摊掉。最后我们得到了：

\Theta(1)+\Delta\Phi(S)<3(\Phi(x')-\Phi(x))

这再度印证了我们的猜测：将经势能函数均摊后的时间花费写成差分的形式，且常数为 0。

3. 之字形旋转

（图源网络，侵权删）

我们对 x p g x' p' g' 的定义仍旧相同，与图中相应字符标注的节点所处位置对应。

这里 \Delta\Phi(S)=\Phi(x')+\Phi(p')+\Phi(g')-\Phi(x)-\Phi(p)-\Phi(g)。同样，我们发现 \Phi(g)=\Phi(x')，则 \Delta\Phi(S)=\Phi(p')+\Phi(g')-\Phi(x)-\Phi(p)

照此步骤做下去，我们可以发现 \Delta\Phi(S)<\Phi(x')+\Phi(g')-2\Phi(x) 依然成立，但是，最关键的步骤 \text{siz[x']}> \text{siz[x]}+\text{siz[g']} 并不一定成立。所以，不能草率地认为“完全一样”。

但是，相差也并不大。读者可以自己试着推一下加深理解。详细过程在第六节给出。

4. 整合

将之前所有求得的不等式累加起来。由于 2 节推出的不等式式的差分系数为3，所以可以将第一个单旋的系数也化为 3，可以证明 \Theta(1)+(\Phi(x')-\Phi(x))<\Theta(1)+3(\Phi(x')-\Phi(x))，不再赘述。

由此，由于后一个操作的 x 就是前一个操作的 x'，所以可以证明访问单个节点的总用时均摊后满足 T(n)<\Theta(1)+3(\Phi(x_{root})-\Phi(x_{beginning}))，即 T(n)=\Theta(\log n)。

Q.E.D.

5. 为啥不能用单旋

如果在一字型旋转的时候没有遵循先转父亲再转自己的顺序，而是一路单旋，会有什么后果？

（图P自网络，侵权删）

我们可以看到，关键性质 \text{siz[x']}>\text{siz[x]}+\text{siz[g']} 并不成立。同时，也无法找出一个类似的关键性质。事实上，在成链的时候，单旋链底并不会造成链深度的减少，也就是说时间复杂度可能会被卡成 \Theta(n^2)。

6. 之字形旋转完整证明

（图源网络，侵权删）

证明源自性质。在一字型旋转的时候，我们找到了 \text{siz[x']}>\text{siz[x]}+\text{siz[g']} 这一关键性质。在这个旋转中，该性质并不成立，但是我们可以找到一个替代的关键性质 \text{siz[x']}> \text{siz[p']}+\text{siz[g']}。

所以，我们可以将 \Delta\Phi(S) 变化为

对于其对应的式子 $\Phi(p')+\Phi(g')-2\Phi(x')$，由于 $\text{siz[x']}>\text{siz[p']}+\text{siz[g']}$，我们可以按和上面完全相同的方法得到 $\Phi(p')+\Phi(g')-2\Phi(x')<-1$。 所以，调整后的时间复杂度为： $$\Theta(1)+\Delta\Phi(S)<\Theta(1)+\Phi(p')+\Phi(g')-2\Phi(x)-1-(\Phi(p')+\Phi(g')-2\Phi(x'))$$ 整理，变为： $$\Theta(1)+\Delta\Phi(S)<2(\Phi(x')-\Phi(x))$$ 证毕。 # 拓展-并查集 ## 1.如何卡并查集 实际上，单纯路径压缩并查集的最坏时间复杂度不是 $\Theta(n\alpha(n))$。 我们构造一颗二项树（实际上和一般的二项树不太一样），其中 `j` 是常数，$T_k$ 为一个 $T_{k-1}$ 加上一个 $T_{k-j}$ 作为根节点的儿子。  边界条件，$T_1$ 到 $T_j$ 都是一个单独的点。 如果我们展开就会发现，可以有两种不同的展开形式。一种是沿着右节点展开，先展开 $T_{k-j}$ 的子树，再展开 $T_{k-2j}$，以此类推，得到图 4。还有一种是沿着 $T_{k-j}$ 的父节点展开，先展开 $T_{k-j-1}$，再展开 $T_{k-j-2}$，得到图 5 。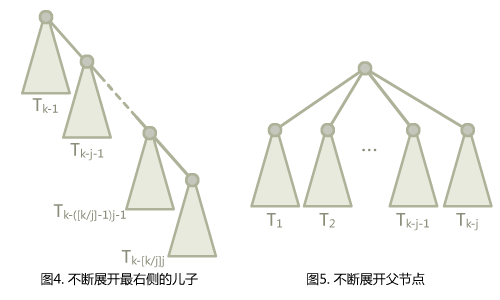  右边是不是特别像左边访问 $T_{k-[k/j]j}$ 的根节点后路径压缩过后的形式？不，他不是，因为节点的标号不对。左边的节点标号每棵树都差 `j`，而右边的节点标号每个树只差 `1`。 那么如何展开图5，才能愉快地卡并查集呢？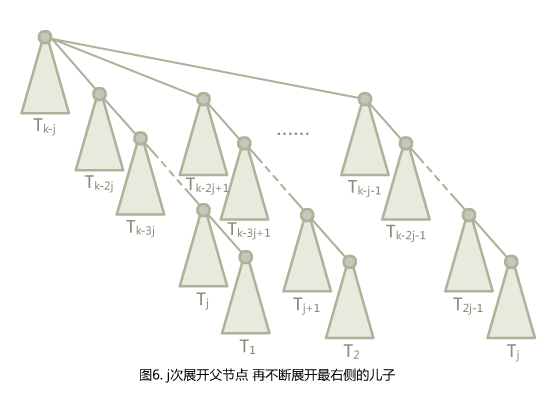  在这里，你会发现，如果按次序访问最底下 $T_1$，$T_2$，$T_3$……，$T_j$ 的根，再在最顶上放一个根节点让他们挂到上面来，会得到图 5 的形式。实际上，根上还会再挂一个点，不过这不重要。 可以证明，$T_k$ 的点数为 $(j+1)^{\frac{k}{j}-1}$。取 $j=\lfloor\frac{m}{n}\rfloor$，$i=\lfloor\log_{j+1}\frac{n}{2}\rfloor$，$k=ij$，就可以得到 $T_k=(j+1)^{i-1}=\lfloor\frac{n}{2}\rfloor$。只需要将访问分成 $\frac{n}{2}$ 组，每组都挂个根节点，访问最底下的 $j=\lfloor\frac{m}{n}\rfloor$ 个点，就可以把不带秩合并的并查集卡到 $\Omega(m\log_{1+\frac{m}{n}}n)$，$\Omega$ 表示运行时间的下界。 附[P3367并查集](https://www.luogu.org/problem/P3367) Hack 数据生成器： ```cpp #include <cmath> #include <cstdio> #include <cstdlib> using namespace std; int mlog(int x,long double k) { return (int)(log(k)/log(x)); } int n; int dtop; int ndot() { if(dtop<n) { ++dtop; return dtop; } else { return rand()%n+1; } } char out[15]; FILE* ot; int m; int connect(int i,int j) { --m; fprintf(ot,"1 %d %d\n",j,i); return i; } int mi[1000005]; int mtop; int buildt(int k,int j,int m) { if(k<j) { if(m) { ++mtop; mi[mtop] = ndot(); return mi[mtop]; } return ndot(); } int lr = buildt(k-j,j,m); int rr = buildt(k-1,j,0); return connect(rr,lr); } int mbuild(int k,int j) { int root = buildt(k-j,j,0); for(int i=1; i<=j; ++i) { root = connect(root,buildt(k-j-i,j,1)); } return root; } void init() { scanf("%s",out); ot = fopen(out,"w"); srand(20040703); } int main() { init(); scanf("%d%d",&n,&m); fprintf(ot,"%d %d\n",n,m); int j = m/n; int i = mlog(j+1,n/2.0)+1; int k = i*j; int rt = mbuild(k,j); while(m>1) { int nrt = ndot(); fprintf(ot,"1 %d %d\n",rt,nrt); --m; for(int i=1; m&&i<=(j>>1); ++i) { fprintf(ot,"2 %d %d\n",mi[i*2-1],mi[i*2]); --m; } if(m&&j&1) { fprintf(ot,"2 %d %d\n",mi[j],mi[j]); --m; } rt = nrt; } if(m) { fprintf(ot,"%d %d %d\n",rand()%2+1,rand()%n+1,rand()%n+1); } fclose(ot); } ``` `m,n` 可自由输入，要求 $m\geq n$，被卡的是——当前的所有只带路径压缩不带按秩合并的并查集（几乎是当前所有并查集），虽然在那个输入规模下卡不掉。外加一点，这里要求合并操作的实现方式是 `fa[find(a)]=find(b)` 形式的。 对了还有卡的效率。为了不影响阅读，成果在附录附上。 ## 2.如何证并查集 这里，先给出 $\alpha(n)$ 的定义。为了给出这个定义，先给出 $A_k(j)$ 的定义。 定义 $A_k(j)$ 为： $$A_k(j)=\left\{\begin{aligned}&j+1&&k=0&\\&A_{k-1}^{(j+1)}(j)&&k\geq1&\end{aligned}\right.$$ 这里，$f^i(x)$ 表示将 $f$ 连续应用在 $x$ 上 $i$ 次，即 $f^0(x)=x$，$f^i(x)=f(f^{i-1}(x))$。 再定义 $\alpha(n)$ 为使得 $A_{\alpha(n)}(1)\geq n$ 的最小整数值。注意，有些文献可能会描述为 $A_{\alpha(n)}(\alpha(n))\geq n$，反正他们的增长速度都很慢，值都不超过 4。 ### (1).基础定义 每个节点都有一个 `rank`。注意，这里的 `rank` 不等于 `size`。节点的初始 `rank` 为 `0`，在合并的时候，如果两个节点的 `rank` 不同，则将 `rank` 小的节点合并到 `rank` 大的节点上，并且不更新大节点的 `rank` 值。否则，随机将某个节点合并到另外一个节点上，将根节点的 `rank` 值 `+1`。这里的 `rank` 给出了一个深度的上界。记 `x` 的 `rank` 为 $rnk(x)$，类似的，记 `x` 的父节点为 $fa(x)$。我们总有 $rnk(x)+1\leq rnk(fa(x))$。 为了定义势函数，需要预先定义一个辅助函数 $level(x)$。其中，$level(x)=\max(k:rnk(fa(x))\geq A_k(rnk(x)))$。当 $rnk(x)\geq1$ 的时候，再定义一个辅助函数 $iter(x)=\max(i:rnk(fa(x))\geq A_{level(x)}^i(rnk(x))$。这些函数定义的 $x$ 都满足 $rnk(x)>0$ 且 $\text{x不是某个树的根}$。 上面那些定义可能让你有点头晕。再理一下，对于一个 $x$ 和 $fa(x)$，如果 $rnk(x)>0$，总是可以找到一对 $i,k$ 令 $rnk(fa(x))\geq A_k^i(rnk(x))$，而 $level(x)=\max(k)$，在这个前提下，$iter(x)=\max(i)$。$level$ 描述了 $A$ 的最大迭代级数，而 $iter$ 描述了在最大迭代级数时的最大迭代次数。 对于这两个函数，$level(x)$ 总是随着操作的进行而增加或不变，如果 $level(x)$ 不增加，$iter(x)$ 也只会增加或不变。并且，它们总是满足以下两个不等式： $$0\leq level(x)<\alpha(n)$$ $$1\leq iter(x)\leq rnk(x)$$ 考虑 $level(x)$、$iter(x)$ 和 $A_k^j$ 的定义，这些很容易被证明出来，就留给读者用于熟悉定义了。 定义势能函数 $\Phi(S)=\sum\limits_{x\in S}\Phi(x)$，其中 $S$ 表示一整个并查集，而 $x$ 为并查集中的一个节点。定义 $\Phi(x)$ 为： $$\Phi(x)=\left\{\begin{aligned}&\alpha(n)\times rnk(x)&&rnk(x)=0\text{ 或 x为某棵树的根节点}&\\&(\alpha(n)-level(x))\times rnk(x)-iter(x)&&otherwise&\end{aligned}\right.$$ 然后就是通过操作引起的势能变化来证明摊还时间复杂度为 $\Theta(\alpha(n))$ 啦。注意，这里我们讨论的 $union(x,y)$ 操作保证了 $x$ 和 $y$ 都是某个树的根，因此不需要额外执行 $find(x)$和$find(y)$。 可以发现，势能总是个非负数。另，在开始的时候，并查集的势能为 $0$。 ### (2).$union(x,y)$ 操作 其花费的时间为 $\Theta(1)$，因此我们考虑其引起的势能的变化。 这里，我们假设 $rnk(x)\leq rnk(y)$，即 $x$ 被接到 $y$ 上。这样，势能增加的节点仅有 $x$（从树根变成非树根)，$y$（秩可能增加）和操作前 $y$ 的子节点（父节点的秩可能增加）。我们先证明操作前 $y$ 的子节点 $c$ 的势能不可能增加，并且如果减少了，至少减少 $1$。 设操作前 $c$ 的势能为 $\Phi(c)$，操作后为 $\Phi(c')$，这里 $c$ 可以是任意一个 $rnk(c)>0$ 的非根节点。我们分三种情况讨论。 1. $iter(c)$ 和 $level(c)$ 并未增加。显然有 $\Phi(c)=\Phi(c')$。 2. $iter(c)$ 增加了，$level(c)$ 并未增加。这里 $iter(c)$ 至少增加一，即 $\Phi(c')\leq \Phi(c)-1$，势能函数减少了，并且至少减少 1。 3. $level(c)$ 增加了，$iter(c)$ 可能减少。但是由于 $0<iter(c)\leq rnk(c)$，$iter(c)$ 最多减少 $rnk(c)-1$，而 $level(c)$ 至少增加 $1$。由定义 $\Phi(c)=(\alpha(n)-level(c))\times rnk(c)-iter(c)$，可得 $\Phi(c')\leq\Phi(c)-1$。 所以，势能增加的节点仅可能是 $x$ 或 $y$。而 $x$ 从树根变成了非树根，如果 $rnk(x)=0$，则一直有 $\Phi(x)=\Phi(x')=0$。否则，一定有 $\alpha(x)\times rnk(x)\geq(\alpha(n)-level(x))\times rnk(x)-iter(x)$。即，$\Phi(x')\leq \Phi(x)$。 因此，唯一势能可能增加的点就是 $y$。而 $y$ 的势能最多增加 $\alpha(n)$。因此，可得 $union$ 操作均摊后的时间复杂度为 $\Theta(\alpha(n))$。 ### (3).$find(a)$ 操作 如果查找路径包含 $\Theta(s)$ 个节点，显然其查找的时间复杂度是 $\Theta(s)$。如果由于查找操作，没有节点的势能增加，且至少有 $s-\alpha(n)$ 个节点的势能至少减少 $1$，就可以证明 $find(a)$ 操作的时间复杂度为 $\Theta(\alpha(n))$。为了避免混淆，这里用 $a$ 作为参数，而出现的 $x$ 都是泛指某一个并查集内的结点。 首先证明没有节点的势能增加。很显然，我们在上面证明过所有非根节点的势能不增，而根节点的 $rnk$ 没有改变，所以没有节点的势能增加。 接下来证明至少有 $s-\alpha(n)$ 个节点的势能至少减少 $1$。我们上面证明过了，如果 $level(x)$ 或者 $iter(x)$ 有改变的话，它们的势能至少减少 $1$。所以，只需要证明至少有 $s-\alpha(n)$ 个节点的 $level(x)$ 或者 $iter(x)$ 有改变即可。 回忆一下非根节点势能的定义，$\Phi(x)=(\alpha(n)-level(x))\times rnk(x)-iter(x)$，而 $level(x)$ 和 $iter(x)$ 是使 $rnk(fa(x))\geq A_{level(x)}^{iter(x)}(rnk(x))$ 的最大数。 所以，如果 $root_x$ 代表 $x$ 所处的树的根节点，只需要证明 $rnk(root_x)\geq A_{level(x)}^{iter(x)+1}(rnk(x))$ 就好了，根据 $A_k^i$ 的定义，$A_{level(x)}^{iter(x)+1}(rnk(x))=A_{level(x)}(A_{level(x)}^{iter(x)}(rnk(x)))$。 注意，我们可能会用 $k(x)$ 代表 $level(x)$，$i(x)$ 代表 $iter(x)$ 以避免式子过于冗长。这里，就是 $rnk(root_x)\geq A_{k(x)}(A_{k(x)}^{i(x)}(x))$。 当你看到这的时候，可能会有一种“这啥玩意”的感觉。这意味着你可能需要多看几遍，或者跳过一些内容以后再看。 这里，我们需要一个外接的 $A_{k(x)}$，意味着我们可能需要再找一个点 $y$。令 $y$ 是搜索路径上在 $x$ 之后的满足 $k(y)=k(x)$ 的点，这里“搜索路径之后”相当于“是 $x$ 的祖先”。显然，不是每一个 $x$ 都有这样一个 $y$。很容易证明，没有这样的 $y$ 的 $x$ 不超过 $\alpha(n)-2$ 个。因为只有每个 $k$ 的最后一个 $x$ 和 $a$ 以及 $root_a$ 没有这样的 $y$。 我们再强调一遍 $fa(x)$ 指的是路径压缩之前 $x$ 的父节点，路径压缩之后 $x$ 的父节点一律用 $root_x$ 表示。对于每个存在 $y$ 的 $x$，总是有 $rnk(y)\geq rnk(fa(x))$。同时，我们有 $rnk(fa(x))\geq A_{k(x)}^{i(x)}(rnk(x))$。由于 $k(x)=k(y)$，我们用 $k$ 来统称，即，$rnk(fa(x))\geq A_k^{i(x)}(rnk(x))$。我们需要造一个 $A_k$ 出来，所以我们可以不关注 $iter(y)$ 的值，直接使用弱化版的 $rnk(fa(y))\geq A_k(rnk(y))$。 如果我们将不等式组合起来，神奇的事情就发生了。我们发现，$rnk(fa(y))\geq A_k^{i(x)+1}(rnk(x))$。也就是说，为了从 $rnk(x)$ 迭代到 $rnk(fa(y))$，至少可以迭代 $A_k$ 不少于 $i(x)+1$ 次而不超过 $rnk(fa(y))$。 显然，有 $rnk(root_y)\geq rnk(fa(y))$，且 $rnk(x)$ 在路径压缩时不变。因此，我们可以得到 $rnk(root_x)\geq A_k^{i(x)+1}(rnk(x))$，也就是说 $iter(x)$ 的值至少增加 `1`，如果 $rnk(x)$ 没有增加，一定是 $level(x)$ 增加了。 所以，$\Phi(x)$ 至少减少了 1。由于这样的 $x$ 节点至少有 $s-\alpha(n)-2$ 个，所以最后 $\Phi(S)$ 至少减少了 $s-\alpha(n)-2$ ，均摊后的时间复杂度即为 $\Theta(\alpha(n)+2)=\Theta(\alpha(n))$。 ## 3.为何并查集会被卡 这个问题也就是问，如果我们不按秩合并，会有哪些性质被破坏，导致并查集的时间复杂度不能保证为 $\Theta(m\alpha(n))$。 如果我们在合并的时候，$rnk$ 较大的合并到了 $rnk$ 较小的节点上面，我们就将那个 $rnk$ 较小的节点的 $rnk$ 值设为另一个节点的 $rnk$ 值加一。这样，我们就能保证 $rnk(fa(x))\geq rnk(x)+1$，从而不会出现类似于满地 `complie error` 一样的性质不符合。 显然，如果这样子的话，我们破坏的就是 $union(x,y)$ 函数“y 的势能最多增加 $\alpha(n)$”这一句。 分析一下那个 `Hack` 数据。令 $rnk(T_k)=r_k$，这里我们有 $r_k=(k-1)/j$（证明略）。每轮操作，我们将它接到一个单节点上，然后查询底部的 $j$ 个节点。也就是说，我们接到单节点上的时候，单节点的势能提高了 $(k-1)/j+1$。在 $j=\lfloor\frac{m}{n}\rfloor$，$i=\lfloor\log_{j+1}\frac{n}{2}\rfloor$，$k=ij$ 的时候，势能增加量为 $$\alpha(n)\times((ij-1)/j+1)=\alpha(n)\times((\lfloor\log_{\lfloor\frac{m}{n}\rfloor+1}\frac{n}{2}\rfloor\times \lfloor\frac{m}{n}\rfloor-1)/\lfloor\frac{m}{n}\rfloor+1)$$ 变换一下，去掉所有的取整符号，就可以得出，势能增加量 $\geq \alpha(n)\times(\log_{1+\frac{m}{n}}n-\frac{n}{m})$，`m` 次操作就是 $\Omega(m\log_{1+\frac{m}{n}}n-n)=\Omega(m\log_{1+\frac{m}{n}}n)$。 ## 4.如何知道如何卡并查集 我们不仅需要将大的结构合到小的结构上面，还需要诱导 `find` 操作将提高的势能释放出来。也就是说，我们需要一个结构，可以在路径压缩之后保持其基本不变，最好还能将一个本来 $rnk$ 很高的节点变低。 本来 $rnk$ 最高的节点就是根节点，容易想到可以挂一个孤立根，然后将所有节点都挂上来，同时在路径压缩下能保持结构不变。那说明原本的根下面就有路径压缩过程中所遍历过的所有节点。 由于那个结构最好有无限大小，所以可以考虑递归定义这个结构。如果用 $T_k$ 表示第 $k$ 级的这种结构，它就必须有一个横的方向包括 $T_{k-1}$ 。这样，在路径压缩之后，仍旧是一个根挂着 $T_1$ 到 $T_{k-1}$。 如果我们只压缩一条路径，自然可以在横纵两个方向都定义 $T_{k-1}$，那么 $siz(T_n)=2\times siz(T_{n-1})+1$，也就是说 $siz(T_n)=\Theta(2^n)$。$\log n$ 的时间复杂度，但是没有好好利用所有的查询，这里必须得要有 $m\geq2^k$，最终我们建出来的树不会很大。由于路径压缩之后，是连续且无重复的，那么假如我们要压缩 $j$ 条路径，它们必须是相互错开的。容易想到，可以在纵向的方向定义 $T_{k-j}$。这样，如果横向展开 $j$ 颗子树，再纵向展开，形成的路径就是连续而无重复的。只要合理安排 $j$ 和 $k$ 的值，我们就可以利用好所有的查询。 当然，我们还能得到一个启示：很多算法都是很难卡的，但是 $Tarjan$ 总是知道怎么卡。 ## 5.关于启发式合并 由于按秩合并比启发式合并难写，所以很多 `dalao` 会选择使用启发式合并来写并查集。具体来说，则是对每个根都维护一个 $siz[x]$，每次将 $siz$ 小的合并到大的上面。 所以，启发式合并会不会被卡？ 首先，~~手推一下我们就可以发现那个数据卡不掉启发式合并~~ 可以从秩参与证明的性质来说明。如果 $siz$ 可以代替 $rnk$ 的地位，则可以使用启发式合并。快速总结一下，秩参与证明的性质有以下三条： 1. 每次合并，最多有一个节点的秩上升，而且最多上升 1 2. 总有 $rnk(fa(x))\geq rnk(x)+1

3. 节点的秩不减

关于第二条和第三条，siz 显然满足，然而第一条不满足，如果将 x 合并到 y 上面，则 siz(y) 会增大 siz(x) 那么多。

所以，可以考虑使用 \log_2 siz(x) 代替 rnk(x)。

关于第一条性质，由于节点的 siz 最多翻倍，所以 \log_2 siz(x) 最多上升 1。关于第二三条性质，既得易见平凡。

所以说，如果不想写按秩合并，就写启发式合并好了，时间复杂度仍旧是 \Theta(m\alpha(n))。

总结-从以上几例来看势能函数的构造

我学算法的时候，有一个原则：所有算法都不是天上掉下来的，都是被人想出来的。既然别人能想出来，那么他一定有一个思考过程。既然我没想出来，我就得去复原那个思考过程，去思考这个算法是怎么被想出来的。

势能函数用于衡量均摊的时间。所以，势能函数必须在进行用时短的操作时上升，进行用时长的操作时下降。或者形象化地说，势能函数高的节点或数据结构必然是那些“不平衡的” “操作用时肯定特别长的” “下一次操作就给你调整掉的” “欠干的” 节点或数据结构。

至于并查集的势能函数的构造，是特别巧妙的。由于我们的并查集维护了一个 rnk 值，所以势能函数可能和 rnk 有关。并查集的 unio 操作最多令一个节点的 rnk 加 1，所以可以认为时间复杂度是关于 rnk 的一次函数。而 find 操作则至关重要。它改变了一路上所有节点的父节点。所以，如果有一个函数 F 迭代在节点上，F(x)=x+1，非根节点的势能 \Phi'(x)=rnk(x)-i，那么就可以通过函数的迭代次数的减少来降低势能。但是这里不能保证势能函数非负。

既然不能保证势能函数非负，就可以通过更猛的迭代函数来减少所需要的迭代次数，从而让势能函数为正的。也就是说，我们不能让 F^{x+1}(x) 在我们定义的用于迭代的函数那里出现。那么就可以定义出一个升级规则，让 F_{k-1}^{i+1}(i)=F_k(1)。这里，我们就得到了 A_k^i 的定义，之后就水到渠成了。如果尝试算算，就会发现，哦豁，小家伙涨得挺快。

而且，势能函数必然和其对应的数据结构有直接且强烈的关联。比如并查集的势能函数，就涉及到并查集操作中维护的 rnk；单调队列的势能函数就是单调队列中的元素个数；而 Splay 的势能函数，因为 Splay 并没有什么特殊性质，于是干脆设置成 \Theta(\log |S|) 来避免一系列麻烦的证明（而且对数函数将加法转换为乘法，乘法比加法容易放缩）。因为只有这样，才便于利用数据结构的性质进行证明。

我认为，数据结构的性质可以概括为结构性质和操作性质。势能函数的定义可以体现出数据结构的结构性质，而在数据结构上的操作对势能函数的影响则体现出数据结构的操作性质。

无论多巧妙的证明，它都是基于性质的。如果没有利用好每一条性质、积极地寻找关键性质，而光想证明，就跟无地基而盖高楼，白努力而徒费功。 这是我在之前，在无数次的证明不出和卡壳，以及无数次的看最终证明而恍然大悟中所体会到的。

课后习题

习题1

定义一个数据结构 multi_stack，支持以下操作：

1. push x：往栈里面压入x。
2. pop：弹出栈顶元素
3. multi_pop x：弹出栈顶的x个元素。

其中保证 push 和 pop 的时间复杂度为 \Theta(1)，而 multi_pop x 的实现方式是重复执行 x 次 pop。请给出三个操作的均摊时间复杂度并证明。

习题2

二进制加法计算器，在 1111+1 的时候会改变五个数字的值，修改的数字数量最多达到 \Theta(\log n)，现在假设计算器的修改单个位的操作是 \Theta(1) 的，并且其只支持 +1 操作，请证明这种计算器执行 +1 操作的时间复杂度是均摊 \Theta(1) 的。

习题3

理解此篇博客中的时间复杂度证明，并给出证明的完整版。

习题4

课后了解均摊时间复杂度分析的另外两种方法：核算法（accounting method）与 聚合分析法。

习题5

给出一个有 n 个元素的数列，求他们的最大公约数（GCD），采用以下算法：

gcd(a,b) = if b==0 return a;
              else return gcd(b,a%b)

int main()
   ans = a[1]
   for(int i=2; i<=n; ++i)
       ans = gcd(ans,a[i])

（伪代码）

求这个算法的时间复杂度，并给出证明。

习题6（拓展题）

请理解替罪羊树的时间复杂度证明，并尝试从操作出发自己证明一遍。

参考资料

• Splay时间复杂度证法参考1（证法似乎是伪的）
• Splay时间复杂度证法参考2（阅读文本建议将 \[ 和 \] 替换为 $$，\( 和 \) 替换为 $，‘ 替换为 '，然后在洛谷博客中阅读）
• 可看的证法参考（感谢小粉兔大佬提供）
• Splay图源
• 算法导论（第21章）
• 如何卡路径压缩并查集 -Canopus_wym
• 如何卡路径压缩并查集 -MoebiusMeow

附录-卡得咋样

参与卡人的数据生成器：

见上

被卡的程序：

#include <cstdio>
using namespace std;

int getint()
{
    char c;
    while((c=getchar())<'0' || c>'9')
    {
        ;
    }
    int x = c^'0';
    while((c=getchar())>='0' && c<='9')
    {
        x = (x*10)+(c^'0');
    }
    return x;
}

int st[10000005];

int getfa(int x)
{
    return x==st[x]?x:st[x]=getfa(st[x]);
}

int main()
{
    int n = getint();
    int m = getint();
    for(int i=1; i<=n; ++i)
    {
        st[i] = i;
    }

    for(int i=1; i<=m; ++i)
    {
        int cmd = getint();
        int a = getint();
        int b = getint();

        if(cmd==1)
        {
            st[getfa(a)] = getfa(b);
        }
        else
        {
            putchar(getfa(a)==getfa(b)?'Y':'N');
            putchar('\n');
        }
    }
}

对比程序：

#include <cstdio>
using namespace std;

int getint()
{
    char c;
    while((c=getchar())<'0' || c>'9')
    {
        ;
    }
    int x = c^'0';
    while((c=getchar())>='0' && c<='9')
    {
        x = (x*10)+(c^'0');
    }
    return x;
}

int st[10000005];
int rnk[10000005];

int getfa(int x)
{
    return x==st[x]?x:st[x]=getfa(st[x]);
}

int main()
{
    int n = getint();
    int m = getint();
    for(int i=1; i<=n; ++i)
    {
        st[i] = i;
    }

    for(int i=1; i<=m; ++i)
    {
        int cmd = getint();
        int a = getint();
        int b = getint();

        if(cmd==1)
        {
            int fa = getfa(a);
            int fb = getfa(b);
            if(rnk[fa]>rnk[fb])
            {
                st[fb] = fa;
            }
            else if(rnk[fa]==rnk[fb])
            {
                st[fb] = fa;
                ++rnk[fa];
            }
            else
            {
                st[fa] = fb;
            }
        }
        else
        {
            putchar(getfa(a)==getfa(b)?'Y':'N');
            putchar('\n');
        }
    }
}

将输入、输出语句重定向以后作为评判双方。

裁判：

#include <ctime>
#include <cstdio>
#include <cstdlib>
using namespace std;

void run(const char* runexe,const char* printas)
{   
    clock_t start = clock();
    for(int i=1; i<=100; ++i)
    {
        system(runexe);
    }
    clock_t end = clock();

    printf("%s runtime = %d tic-tac %.2Lf ms\n",printas,end-start,1.L*(end-start)/CLOCKS_PRE_SEC*1000);
    fprintf(ot,"%s runtime = %d tic-tac %.2Lf ms\n",printas,end-start,1.L*(end-start)/CLOCKS_PRE_SEC*1000);

}

int main()
{
    FILE* ot = fopen("cmd.in","w");
    FILE* result = fopen("res.out","w");

    int n,m;
    printf("input n,m:");
    scanf("%d%d",&n,&m);
    fprintf(ot,"t4.in\n%d %d\n",n,m);

    int i = 0;

    system("hacker.exe");

    run("hacked.exe","hacked");
    run("unhack.exe","unhack");
}

成果：

当 n=m 的时候，两个程序的运行时间无差异。

当 n=5\times10^5，m=10^6 时，被 hack 的程序爆栈了，另一个程序跑了 89284 ms（重复跑一百遍的总时间）。

当 n=5\times10^4，m=10^5 时，被 hack 的程序跑了 9419ms，另一个程序跑了 9227ms。这里虽然看似有两百毫秒的差别，但是由于被放大了，所以实际上单次运行的差别只有几毫秒。当然，由于数据规模小，所以差别也小。

当 n=10^5，m=2\times 10^5 时，被 hack 的程序爆栈了。

总结，如果 n,m\leq 10^7 的时候，似乎真的有可能放加路径压缩和按秩合并的过，卡掉只加路径压缩的。