学图论，你真的了解最短路吗？

给我的上一篇打个广告洛咕日报#18 简单食用的博弈论希望能够有所收获w

为了写这篇文章，我这个蒟蒻真的已经拿出了自己全部压箱底的图论知识，希望大家能够支持，谢谢大家喷轻点

$update\ on\ 2019.7.16$ 发现自己学不会$k$短路正解之后赶来口胡（ $update\ on\ 2019.7.31$ 新增一道例题 $update\ on\ 2019.7.31$ 增加卡常技巧、最长路和分层图 $update\ on\ 2019.8.6$ 应@[夜猫子驱蚊器](https://www.luogu.org/space/show?uid=6174)的要求，增加$pb\_ds\ Dijkstra $update\ on\ 2020.7.4$ 知乎评论指出一个锅，现已经修复 $update\ on\ 2020.10.8$ 修复一些 $bug

汉字字母和数字之间的空格的锅太难修了，反正不影响阅读，先咕着吧

修了修了，我不咕了

感谢@亲爱的王先生和@Jelly_Goat对文章修改提出建议，以及@HyyypRtf06提出画图建议

图论，堪称算法界大魔王之一，那么最短路就是大魔王的战斗机——出题灵活，难度可大可小（可以是模板，也可以现身在 NOI 考场），细节巨多，有些算法还可以被卡，是各位 Oier 们学习的重点之一，今天介绍一些常用的最短路算法，希望对大家有一定帮助

------------ ## $1.$如何建图 > 要跑最短路，首先要有图 ——~~鲁迅~~ 我们知道，最短路是以图为基础的，有了一个图，我们才能跑最短路，那么如何将一个二维的图，转化为数据存储呢？ 目前常用的存储方法有两种，分别是[邻接矩阵](https://baike.baidu.com/item/%E9%82%BB%E6%8E%A5%E7%9F%A9%E9%98%B5/9796080)（用二维数组表示边）和[邻接表](https://baike.baidu.com/item/%E9%82%BB%E6%8E%A5%E8%A1%A8)（模拟链表表示边）两种，他们各有不同的优势和不足： | | 邻接矩阵（暴力） | 邻接表（类似链表） | | :----------: | :----------: | :----------: | | **使用范围** | 稠密图 | 主要是稀疏图 | | **空间耗费** | $n^2$（$n$为点个数） | 理论上是$e$（$e$为边条数） | | **实现方式** | 二维数组 | 数组模拟链表、$vector$ | 通常来讲，在数据范围足够小时，我们采用邻接矩阵，而数据范围大时采用邻接表 邻接矩阵实现： 无权图： ```cpp int main() { cin>>n>>m; while(m--) { int x,y; cin>>x>>y; g[x][y]=1;//g[x][y]=1表示x到y有一条边连接 //g[y][x]=1;//去掉注释后是无向图 } return 0; } ``` 带权图： ```cpp int main() { cin>>n>>m; while(m--) { int x,y,w; cin>>x>>y>>w; g[x][y]=w;//g[x][y]=w表示x到y有一条权值为w的边 //g[y][x]=w;//去掉注释后是无向图 } return 0; } ``` 邻接表实现： $PS$：将不给出无权图代码，请大家自行思考 数组（[链式前向星](https://baike.baidu.com/item/%E5%89%8D%E5%90%91%E6%98%9F)）： 以一个点为基础，后面跟一个链表，依次连着每一条以该点为起点的边  我们用数组+结构体模拟一个链表，用$p$作为数组下标，每次新建一条边就把它加入数组数组下标后移一个，存入终点和权值 但是为了实现链~~婊~~表的结构，我们还要加上一个后继指针存它的下标，同时开一个头指针数组 $h[]$，初始化为 $h[i]=i$ 记录每一个点的头指针，然后每当有新的边时就让新的边的后继指针指向 $e[h[i]]$，然后把 $h[i]$ 换成当前边的数组下标，就完成了存图过程 ```cpp struct edge { int v,w,nxt; }e[1001]; int h[1001]; inline void add(int a,int b,int c) { e[++p].nxt = h[a];//h[a]是a的上家 h[a] = p;//更新上家 e[p].v = b;//这是边的终点 e[p].w = c;//存权值 } int main() { cin>>n>>m; while(m--) { int x,y,w; cin>>x>>y>>w; add(x,y,w);//连接 //add(y,x,w);//去掉注释是双向 } return 0; } ``` $vector$（需要用结构体辅助）： ```cpp struct edge { int node,weight; edge(int node_,int weight_)://构造函数，让我们可以直接给结构体赋值 node(node_),weight(weight_){} };//结构体 vector<edge> v[1001]; int n,m; int main() { cin>>n>>m; while(m--) { int x,y,w; cin>>x>>y>>w; v[x].push_back(edge(y,w));//模拟链表，存边 //v[y].push_back(edge(x,w));//双向 } return 0; } ``` 接下来我们要开始谈最短路算法了，请站稳扶好（ ------------ ## $2.dfs$——小规模万能暴力算法 $dfs$，学名深度优先搜索，可以解决较小图中的最短路，是一种单源最短路算法 $dfs$ 的核心思想是顺着一条路一直走下去，不撞南墙不回头，直到遍历所有情况 这就好比是走迷宫，你沿着一条路要一直走，直到遇到死胡同才返回 通常采用邻接矩阵存储，有权无权都可以处理，可以处理负边权，但不能处理负环 简单来说就是从一个点出发，递归+回溯遍历每一条与它相连的边，到达每个点，更新最短路 虽然代码很好写，但是极容易超时，请谨慎食用此算法 代码（无权图）： ```cpp void dfs(int x,int step) { dis[x]=step;//更新数据 for(int i=1;i<=n;++i) if(g[x][i]) { g[x][i]=0; dfs(i,step+1); g[x][i]=1; } } ``` 写 $dfs$ 也可以用邻接表，显然在稀疏图中有一定优势，但是由于用 $dfs$ 的题数据规模本来也不大，所以优势不够明显，很少有人用邻接表做 $dfs$ ~~毕竟邻接表不好写呀~~ ------------ ## $3.bfs$——不那么暴力的无权图暴力算法 $bfs$，学名广度优先搜索，可以解决无权图的最短路问题，是一种单源最短路算法，通常用邻接表存图（邻接矩阵当然也可以，但是会慢很多，也容易 $MLE$，因此在此算法中不常用） $bfs$ 可以处理数据规模更大一些的情况，相比来讲，它的代码比 $dfs$ 难写一些，需要队列辅助，思路是每次从队列头部取出一个点，如果访问过就扔掉，否则标记，然后遍历每一个从该点可以直接到达的点加入队列，直到搜到目标点。 这是处理无权图最短路最快捷的算法 $bfs$ 好比是地毯式搜索，先把近处找遍，再一圈圈扩张搜索 $bfs$ 还有一个特点，就是不会重复经过第一个节点第二次，因为队列中靠前的点（先被搜到的点）一定比靠后的点（后被搜到的点）的步数要大（或相等），而$bfs$又是处理无权图的算法，我们便得出一个小学生推导： $$∵a≤b$$ $$∴a+1≤b+1$$ ~~精彩，真精彩！~~ 所以我们得出一个点只要被搜到一次，那一定就是它的最短路径 接下来我们分析一下 $bfs$ 的时间复杂度：它有遍历到目标点一次就可以输出，随时跳出算法结束程序的特性，所以它的时间复杂度是不稳定的，最好情况是 $O(1)$（就是起点和终点是同一个点的情况），最坏情况是 $O(n+e)$（目标点是最后一个被搜到的点的情况） 给出代码（本人喜欢用 $STL$ 写图论，这里给的是 $queue$ 代码，队列也可以手写，代码可以去网上搜一搜 qwq）： ~~然而现在已经喜欢用手写前向星了~~ ```cpp queue<pair<int,int> > q;//前面是点编号，后面是步数 q.push(make_pair(s,0));//起始点 while(!q.empty())//如果队列不空就说明还有点没有搜到，就继续搜 { int k=q.front().first,step=q.front().second(); q.pop(); if(k==f)//如果找到终点直接结束 { cout<<step<<endl; return 0; } if(vis[k]) continue;//利用特性，如果已经访问过就不再浪费时间 vis[k]=1;//标记 for(vector<int>::iterator it=v[k].begin();it!=v[k].end();++it)//定义一个迭代器遍历所有与当前点相连的点vector是上文的邻接表 q.push(make_pair(*it,step+1));//把这个点压入队列 } ``` ### 拓展：二维矩阵中的 $bfs

这其实才是正宗 bfs，上面才是拓展好不好

看上面的代码是不是有点奇怪（滑稽

是不是觉得不像是你熟悉的 bfs

大家初学时接触的 bfs 应该是在二维矩阵中的 bfs

它往往输入一个矩阵：

001
101
100

然后告诉你不同数字代表什么意思，你可以怎么走（四向搜还是八向搜）并告诉你起始点和结束点让你求最短距离

这个。。。它显然是无权的，但是没有边了。。。

毛主席说得好：自己动手，丰衣足食

我们要自己建造一个图！

以四向搜为例，其实一个点能走的路无非上下左右四种，根据数组坐标很容易可以得出四种移动的位移坐标（\{x,y\}表示从上一点向下移动 x 步，向右移动 y 步）：

上 \{-1,0\}；下 \{1,0\}；左 \{0,-1\}；右 \{0,1\}

PS：与平面直角坐标系不同，二维矩阵通常用前面坐标表示纵坐标，后面坐标表示横坐标，下加上减，右加左减

然后我们就珂以把四个坐标的横纵坐标分开存进两个数组里，然后开一个循环搜索，就可以解决了 qwq

代码（核心部分）：

const int dx[]={-1,1,0,0},dy[]={0,0,-1,1};//位移数组
while(!q.empty())//如果队列不空就说明还有点没有搜到，就继续搜
{
    .......
    for(int i=0;i<4;++i)
    {
        int xx=x+dx[i],yy=y+dy[i];//找到新的点的坐标
        if(xx<=0||xx>n||yy<=0||yy>n||vis[xx][yy])//二维矩阵要特判是否越界
            continue;
        q.push(xx);
        q.push(yy);
    }
}

4.串场——给你一个见偶像的机会

如果你轻松的学习了上述两个算法，那么恭喜你，我们可以开始学习正宗的最短路啦（鼓掌鼓掌！(〃'▽'〃)

我们掌声有请代码天团最短路 F4 闪亮登场！【尖叫声】

好，现在你已经认识它们了，我们来逐一学习吧(￣▽￣)／

上面这一段现在看起来好憨啊

5.Floyd——明明是 DP，却最暴力

这是一个非同一般的算法(/≧▽≦)/

为什么咩？

因为它慢

因为这是唯一的多源最短路算法，用邻接矩阵存储，可以处理负边权，但不能处理负环。多源最短路就是说只要跑一次，任意两点的最短路都能求啦(￣︶￣)，而其他单源最短路跑一次只能得出一个点到其他点的最短路

接下来要讲它的思路，前方过于暴力请坐稳扶好，收起小桌板，打开遮光板，调直座椅靠背，洗手间暂停使用

用邻接矩阵存最短路（dis[i][j] 表示 i 到 j 的最短距离）开一个三重循环（！）外层枚举中间点，中间枚举起点，内层枚举终点，当三个点互不相同时进行松弛操作，如果经过中间点之后的路程和比原路程短，就更新距离，一轮过后，我们得到了一个新的矩阵，然后我们把中间点换成下一个点，再次松弛，的到一个新的矩阵，执行 n 次之后，第 n 个矩阵就是我们的答案啦

由于有三重循环，每层都是 n 轮，时间复杂度为 O(n^3)，虽然在稠密图中优势明显，但是对于稀疏图则占不到一点便宜，是一个虽然不是暴力但是比暴力还暴力的算法，依然是谨慎食用，以免超时，数据范围在 n≤280 还是比较保险的

记得 dis 数组要初始化成正无穷，否则松弛会失效

代码：

//提前将邻接矩阵存在dis数组里，其他不连通的地方初始化成无穷大
for(int k=1;k<=n;++k)//枚举中间点
    for(int i=1;i<=n;++i)//枚举起点
        if(i!=k)//节省时间，如果一样就不往下走
            for(int j=1;j<=n;++j)//枚举终点
                if(i!=j&&j!=k)//继续判断，如果有一样的就不往下走
                    dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);//状态转移方程，也就是所谓的松弛操作

把这个代码稍作修改，就能得到无权图的代码

拓展：探寻 Floyd 的本质

这回是真的拓展了

不是复读机

大家请看这道题：P1119 灾后重建

看完什么感觉？

有那么一瞬间，我也是这样的。。。

难道要 LCT 强制在线？

先别急着懵逼，我们抛开这题不管，先把 Floyd 的本质处理好

根据上面的代码，我们知道外层循环是一个中间点，也是生成矩阵的次数，那么我们就可以把外层循环叉掉啊♂，数组多开一维，用 dis[k][i][j] 表示 i 和 j 之间可以通过编号为 1\dots k 的节点的最短路径

显然，dis[0][i][j] 就是原始邻接矩阵数据

根据上面给出的 Floyd 代码和 dis 数组的定义，我们可以得出一个状态转移方程：

dis[k][i][j]=min(dis[k-1][i][j],dis[k-1][i][k]+dis[k-1][k][j])

所以 Floyd 的本质其实是个 DP！

只不过我们通常做题时利用了数据只会使用一次性的原理，把 dis 变成滚动数组，减少了一维，节省空间

只要我们能够利用 DP 特性，就能解决许多问题

再回来看这道题，文中说每个村子是不同时间修好的，而每个节点都按顺序给出，这不就是恰好相当于 Floyd 的中间点吗？我们可以把 k 轮 DP 分开做，每输入一个点，就用这个点当中转站把最短距离更新一遍，也就是跑一遍 DP。想到这里，这题就基本解决了，根本不用在线之类的神仙操♂作还不是我不会

代码就是这样啦，小细节会注释的(^▽^)看见没，还是吸了氧：

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstring>
#include<vector>
#include<queue>//那时我年少轻狂打了这么多头文件【捂脸】
#define For(i,l,r) for(int i=l;i<=r;++i)//居然还用了宏定义【捂脸】
using namespace std;
const int INF=0x1fffffff;
int dis[201][201];
int n,m,t[201],q;
inline int read()//快读板子
{
    int x=0;
    char c=getchar();
    while(c<'0'||c>'9')
        c=getchar();
    while(c>='0'&&c<='9')
    {
        x=(x<<1)+(x<<3)+c-'0';
        c=getchar();
    }
    return x;
}
int main()
{
    ios::sync_with_stdio(false);//居然还玄学加速【捂脸】
    n=read(),m=read();
    memset(dis,127/3,sizeof(dis));//初始化
    int inf=dis[0][0];
    For(i,1,n)
        dis[i][i]=0;//自己到自己的距离是0,
    For(i,1,n)
        t[i]=read();
    For(i,1,m)
    {
        int x,y,w;
        x=read(),y=read(),w=read();
        dis[x+1][y+1]=dis[y+1][x+1]=w;//因为村庄编号有0，为了处理方便，坐标向后移一个位置
    }
    q=read();
    int k=1;
    while(q--)
    {
        int x,y,w;
        x=read(),y=read(),w=read();
        for(;t[k]<=w&&k<=n;++k)//如果询问的天数没有被处理到就以在k以前修好的村庄为中间点跑Floyd
            for(int i=1;i<=n;++i)
                if(i!=k)
                    for(int j=1;j<=n;++j)
                        if(i!=j&&j!=k)
                            dis[i][j]=dis[j][i]=min(dis[i][j],dis[i][k]+dis[k][j]);//板子
        if(t[x+1]>w||t[y+1]>w)//没修好
            puts("-1");
        else
        {
            if(dis[x+1][y+1]<inf)
                printf("%d\n",dis[x+1][y+1]);//输出距离
            else
                puts("-1");//不连通
        }
    }
    return 0;
}

6.Dijkstra——最短路主流算法

这是目前各大 OIER 们最爱用的最短路算法了， Dijkstra 是单源最短路算法，不能处理带负边权的情况，用邻接矩阵或邻接表存图

下面我们来讲解一下它的思路：

我们找来一个图：

假设它的起点是 a，要求它到各点的最短距离

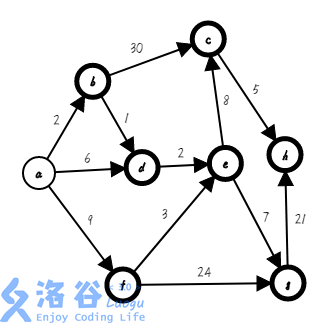
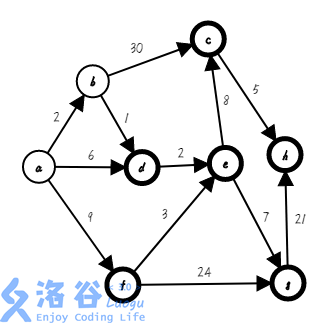
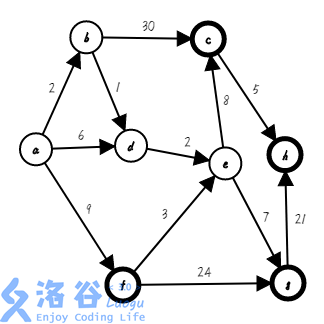
~~接下来图就要变丑了，请注意~~ 第一步，我们先把 $a$ 加入集合，不加粗的点为集合中的点，下同（$s=\{a\}$ ;$dis[]=\{0,∞,∞,∞,∞,∞,∞,∞\}$）：  第二步，我们找出与集合相邻且距离起点最近的点 $b$，把它加入集合，并确定它的最短路 $0+2=2$，存入数组（$s=\{a,b\}$ ;$dis[]=\{0,2,∞,∞,∞,∞,∞,∞\}$）：  第三步，我们找出与集合相邻且距离起点最近的点 $d$，把它加入集合，并确定它的最短路 $2+1=3$，存入数组（$s=\{a,b,d\}$ ;$dis[]=\{0,2,∞,3,∞,∞,∞,∞\}$）：  第四步，我们找出与集合相邻且距离起点最近的点 $e$，把它加入集合，并确定它的最短路 $3+2=5$（$s=\{a,b,d,e\}$ ;$dis[]=\{0,2,∞,3,5,∞,∞,∞\}$）:  第五步，我们找出与集合相邻且距离起点最近的点 $f$，把它加入集合，并确定它的最短路 $0+9=9$（$s=\{a,b,d,e,f\}$ ;$dis[]=\{0,2,∞,3,5,9,∞,∞\}$）:  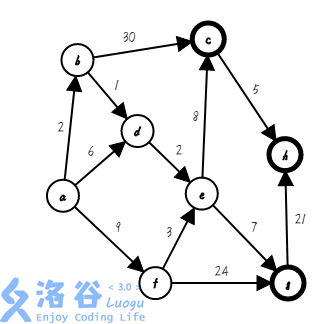第六步，我们找出与集合相邻且距离起点最近的点 $g$，把它加入集合，并确定它的最短路 $5+7=12$（$s=\{a,b,d,e,f,g\}$ ;$dis[]=\{0,2,∞,3,5,9,12,∞\}$）:  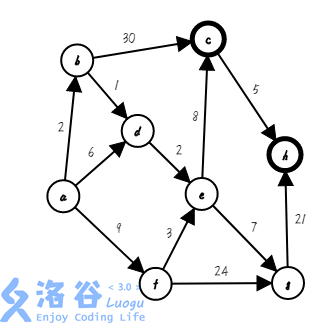第七步，我们找出与集合相邻且距离起点最近的点 $c$，把它加入集合，并确定它的最短路 $5+8=13$（$s=\{a,b,c,d,e,f,g\}$ ;$dis[]=\{0,2,13,3,5,9,12,∞\}$）:  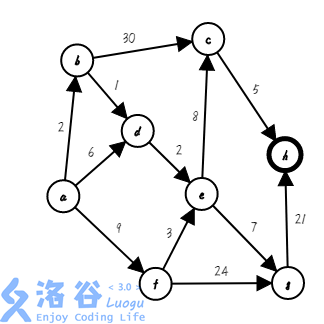第八步，也是最后一步，我们找出与集合相邻且距离起点最近的点 $h$，把它加入集合，并确定它的最短路 $13+5=18$（$s=\{a,b,c,d,e,f,g,h\}$ ;$dis[]=\{0,2,13,3,5,9,12,18\}$）:  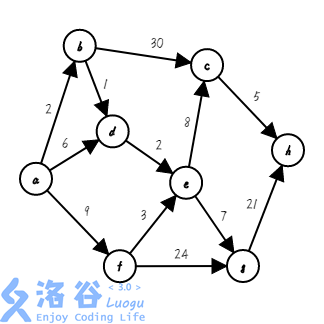至此，整个图的最短路被我们求了出来，$Dijkstra$ 顺利完成！ 理解了它的思路，那么怎么用代码实现呢？ 先用邻接矩阵存储数据，考虑采用一个二重循环，每次寻找出距离集合最近的一个点，然后数组标记它已经加入集合，然后在用当前点对不在集合中的点进行松弛，进行 $n$ 次，整个操作就完成了（此处代码中默认起点是 1） ```cpp void dijkstra() { memset(dis,127/3,sizeof(dis));//初始化 v[1]=1; dis[1]=0; for(int i=1;i<=n;++i) { int k=0; for(int j=1;j<=n;++j)//找出距离最近的点 if(!v[j]&&(k==0||dis[j]<dis[k])) k=j; v[k]=1;//加入集合 for(int j=1;j<=n;++j)//松弛 if(!v[j]&&dis[k]+a[k][j]<dis[j]) dis[j]=dis[k]+a[k][j]; } } ``` 通过上述代码不难发现 $Dijkstra$ 的时间复杂度是 $O(n^2)

个人认为 Dijkstra 是最重要的算法之一，这里推荐几道练手题，可以去做

P1359 租用游艇

P3371 【模板】单源最短路径（弱化版）

P1938 [USACO09NOV]找工就业Job Hunt（有的同学问我这题有负边权怎么用 Dijkstra，可以把一次访问改成最优解剪枝试一试不过这样好像就不是 dij 了）

P1457 城堡 The Castle（这是一道 BFS。但是 Dijkstra 可做，且有一定思维难度，也有一些坑，比如如何取出每一面墙和优先顺序之类的细节也很有趣，在这里特别推荐大家做此题）

拓展1：优化 Dijkstra

以下内容摘自我的另一篇博客

众所周知

Dijkstra$ 复杂度为 $O(n^2)

而且是实打实的 O(n^2)，不会提前结束循环

那么 n 巨大无比怎么办？

 相信大家都知道 $STL$ 里有个东西叫做 $queue

虽然 queue 也可以用 vector 代替

但是这里面有一个逆天的东西叫做 priority\_queue（优先队列）

这个东西是真的好用，自动排序

我们就可以省去松弛和查找操作，直接把节点和数据丢进优先队列，然后最小的就会浮出水面\(^o^)/~并且改用邻接表存储，省去一大些时间和空间

用它来优化 Dijkstra 再合适不过啦

但是这个玩意也有他不友善的一面，不支持在线修改

使用 dis 数组维护集合，更新最小值，可以找到元素直接修改

但是你把它扔进 priority\_queue，当场歇菜

你都找不到这个元素

那怎么办呢？

C++ 真是一门难学的语言

我们不管他，照旧扔新元素进去，但是要用一个数组标记这个东西吐没吐出来，如果下一回吐出来了已经吐过的点直接扔掉就行了

说到这里，我们发现知道距离的同时，还要知道节点编号，这意味着我们扔给 priority\_queue 的应该是一组数据

有的大佬说：用 pair

但是打完程序大概是这个样：

xxx.first...xxx.second
xxx.first
xxx.second
xxx.first
xxx.first
xxx.second
xxx.first...xxx.second

我【数据删除】

鬼知道 first 和 second 是什么东西呀

所以我们不用 pair

自己写结构体

struct queue_element
{
    int x,y,value;
    queue_element(int x_,int y_,int value_):
        x(x_),y(y_),value(value_){}//赋值，没有为什么，背过
};

C++ 真是一门难学的语言

你以为就这样结束了？

CE

然后我们发现 priority\_queue 不认这玩意

因为有两个数据，优先队列不知道应该用哪个数据，什么方法判断大小，所以它不会比较

于是，我们要重载 <，让优先队列明白怎么比较大小

bool operator < (const queue_element &other) const
    {
        return value>other.value;//这样重载是小根堆，因为堆的比较是反过来的-_-||
    }

然后就没问题了

C++ 真是一门难学的语言

inline void dijkstra()//可以不带参数，也可以把起点带进来
{
    priority_queue<element> q;//优先队列大法吼
    q.push(element(1,0));//把起点压进去
    while(!q.empty())//不空就说明还有点没搜完
    {
        element k=q.top();//取出队首
        q.pop();
        if(vis[k.node])//如果已经在集合中（被搜到过）
            continue;//扔掉
        vis[k.node]=1;//标记
        dis[k.node]=k.value;//存下最短路（由于优先队列的排序已经相当于完成了松弛，所以这就是答案）
        for(vector<edge>::iterator it=v[k.node].begin();it!=v[k.node].end();++it)//用指针遍历邻接表
            q.push(element(it->node,it->weight+k.value));//松弛
    }
}

这样一来，均摊时间复杂度降为 O((e+n)logn)，效率大大提升，处理稀疏图所向披靡^_^

拓展2：二维矩阵中的特殊规则最短路建边方法

让我们先来看看这道被大家玩坏了的经典题目吧

P3956 棋盘

住口！我知道你会用 dfs！

现在，我逼迫让你用 Dijkstra 做这道题，怎么办呢？

主体思路没有问题，就是在二维矩阵里跑最短路，二维邻接表做辅助就 OK

主要问题出在如何连边，因为有魔法存在，我们需要给一些不相邻的格子也连上边。。。这可如何是好呢？

难道要用 Dijkstra 套 dfs

对于这种诡异的题目，我们可以把多种情况分割成几部分讨论：

1. 相邻同色格子

直接往邻接表里加一条权值为 0 的边即可

2. 相邻异色格子

直接往邻接表里加一条权值为 1 的边即可

3. 相邻无色格子

现在有点意思了，我们需要考虑一下怎么连，我们可以向这个格子连一条权值是 2 的边。但是由于魔法不能连续使用，导致我们又需要一个额外数组记录魔法是否使用，即使克服了这一问题，也会导致我们无法确定无色格子的颜色而无法继续向外连边，所以这种方法不可行

那么只能考虑用魔法的时候越过无色格子，直接连到目标格子上了

4. 相邻无色格子的相邻有色格子（嗯这个绕口令大家可以多读几遍）

我们可以遇到无色格子进行深入处理，再次搜索无色格子的四周，找有色格子连边（无色的不连，有色的显然可以用两步到达），同色权值为 2，异色权值为 3

至此，建图大功告成

另外我们注意到要把终点旁边（棋盘外）的格子也涂上颜色，而且要涂不同颜色，防止有因为终点无色而无法到达的情况

然后我们跑一个 Dijkstra 搞定√

代码驾到（为锻炼大家的理解能力，此篇代码没有注释，大家可以在 Dijkstra 的模板的基础上加以理解）

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int INF=0x3fffffff;
const int MAX_M=109;
const int dx[]={-1,0,1,0};
const int dy[]={0,-1,0,1};
int m;
int dis[MAX_M][MAX_M];
int chart[MAX_M][MAX_M];
struct edge_t
{
    int x,y,weight;
    edge_t(int x_,int y_,int weight_):
        x(x_),y(y_),weight(weight_){}
};
struct queue_element
{
    int x,y,dis_value;
    queue_element(int x_,int y_,int dis_value_):
        x(x_),y(y_),dis_value(dis_value_){}
    bool operator < (const queue_element &other) const
    {
        return dis_value>other.dis_value;
    }
};
vector<edge_t> edges[MAX_M][MAX_M];
bool xy_valid(int x,int y)
{
    return 1<=x&&x<=m&&1<=y&&y<=m;
}
void add_edge(int x0,int y0,int x1,int y1,int weight)
{
    edges[x0][y0].push_back(edge_t(x1,y1,weight));
}
void add_neighbors(int x,int y)
{
    if(chart[x][y]==0)
        return;
    for(int i=0;i<4;++i)
    {
        int tx=x+dx[i],ty=y+dy[i];
        if(!xy_valid(tx,ty))
            continue;
        if(chart[tx][ty]!=0)
        {
            add_edge(x,y,tx,ty,chart[x][y]==chart[tx][ty]?0:1);
            continue;
        }
        for(int j=0;j<4;++j)
        {
            int ux=tx+dx[j],uy=ty+dy[j];
            if(!xy_valid(ux,uy)||(ux==x&&uy==y)||chart[ux][uy]==0)
                continue;
            add_edge(x,y,ux,uy,chart[x][y]==chart[ux][uy]?2:3);
        }
    }
}
void dijkstra()
{
    priority_queue<queue_element> q;
    q.push(queue_element(1,1,0));
    for(int i=1;i<=m;++i)
        for(int j=1;j<=m;++j)
            dis[i][j]=INF;
    while(!q.empty())
    {
        queue_element t=q.top();
        q.pop();
        if(dis[t.x][t.y]!=INF)
            continue;
        dis[t.x][t.y]=t.dis_value;
        for(vector<edge_t>::const_iterator e=edges[t.x][t.y].begin();e!=edges[t.x][t.y].end();++e)
            q.push(queue_element(e->x,e->y,t.dis_value+e->weight));
    }
}
int main()
{
    int n;
    cin>>m>>n;
    for(int i=0;i<n;++i)
    {
        int x,y,c;
        cin>>x>>y>>c;
        chart[x][y]=c+1;
    }
    ++m;
    chart[m-1][m]=1;
    chart[m][m-1]=2;
    for(int i=1;i<=m;++i)
        for(int j=1;j<=m;++j)
            add_neighbors(i,j);
    dijkstra();
    int ans=min(dis[m-1][m],dis[m][m-1]);
    cout<<(ans==INF?-1:ans)<<'\n';
    return 0;
}

拓展3：pb\_ds\ Dijkstra

重要：前置芝士

我们还可以考虑采用 pd\_bs 封装的优先队列优化 Dijkstra，具体和堆优化区别不大，直接看代码吧

#include<iostream>
#include<cstdio>
#include<vector>
#include<ext/pb_ds/priority_queue.hpp>
using namespace std;
using namespace __gnu_pbds;
struct edge
{
    int node,weight;
    edge(int node_,int weight_):
        node(node_),weight(weight_){}
};
vector<edge> v[100001];
int n,m,s,dis[100001];
bool vis[100001];
inline void dijkstra()
{
    __gnu_pbds::priority_queue<pair<int,int>,greater<pair<int,int> >,pairing_heap_tag> q;
    q.push(make_pair(0,s));
    while(!q.empty())
    {
        pair<int,int> k=q.top();
        q.pop();
        if(vis[k.second])
            continue;
        vis[k.second]=1;
        dis[k.second]=k.first;
        for(vector<edge>::iterator it=v[k.second].begin();it!=v[k.second].end();++it)
            q.push(make_pair(it->weight+k.first,it->node));
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<=m;++i)
    {
        int x,y,w;
        scanf("%d%d%d",&x,&y,&w);
        v[x].push_back(edge(y,w));
    }
    dijkstra();
    for(int i=1;i<=n;++i)
        printf("%d ",dis[i]);
    puts("");
    return 0;
}

改动不大，但是时间效率却有了飞一般的改变(￣▽￣)／

7.Bellman-Ford——负权最短路算法

它的思路如下：给定图 $G(V,E)$（其中 $V$、$E$ 分别为图$G$的顶点集与边集），源点 $s$，数组 $Dis[i]$ 记录从源点 $s$ 到顶点 $i$ 的路径长度，初始化数组$Dis[n]$ 为 $∞$, $Dis[s]$ 为 $0$； 以下操作循环执行至多 $n-1$ 次，$n$ 为顶点数： 对于每一条边 $e(u,v)$ 进行松弛操作，如果 $Dis[u]+w(u,v)<Dis[v]$，则使 $Dis[v]=Dis[u]+w(u,v)$（$w(u,v)$ 为边 $e(u,v)$ 的权值） 若上述操作没有对 $Dis$ 进行更新，说明最短路径已经查找完毕，或者部分点不可达，跳出循环。否则执行下次循环； 为了检测图中是否存在负环路，即权值之和小于 $0$ 的环路。对于每一条边 $e(u,v)$ 额外进行一次松弛，如果松弛成功即不等式 $Dis[u]+w(u,v)<Dis[v]$ 成立，则图中存在负环路，即是说改图无法求出单源最短路径。否则数组 $Dis[n]$ 中记录的就是源点 $s$ 到各顶点的最短路径长度。 那么 $Bellman-Ford$ 用什么存图呢。。。 $emm\dots$ 其实就是用数组+结构体，松弛时遍历边而不是点，然后就能实现，数据结构非常好写，但是代码会难理解一些 ```cpp #include<iostream> #include<cstdio> using namespace std; #define MAX 0x3f3f3f3f//年少轻狂【捂脸】 #define N 100010 long long n,m,s,t; struct edge { long long x,y; long long cost; }; edge v[5*N];//不知道是哪题的数据要求，好像是乱开的大小【捂脸】 long long dis[N]; bool Bellman_Ford() { for(int i=1;i<=n;++i) dis[i]=(i==s? 0:MAX);//初始化 for(int i=1;i<n;++i) for(int j=1;j<=m;++j) { if(dis[v[j].y]>dis[v[j].x]+v[j].cost)//松弛，因为是有向图，方向不能反 dis[v[j].y]=dis[v[j].x]+v[j].cost; } bool flag=1;//标记有无负环 for(int i=1;i<=m;++i) if(dis[v[i].y]>dis[v[i].x]+v[i].cost)//松弛是否成功 { flag=0;//成功则有负环 break; } return flag; } int main() { scanf("%lld%lld%lld%lld",&n,&m,&s,&t);//输入 for(int i=1;i<=m;++i) scanf("%lld%lld%lld",&v[i].x,&v[i].y,&v[i].cost); if(Bellman_Ford())//无负环 printf("%lld\n",dis[t]);//输出 else printf("no\n");//有负环报告错误 return 0; } ``` 二层循环外层需要执行 $n-1$ 次，内层每次执行 $e$（边数）次，才加上判断负环的一层循环最多执行 $e$ 次，时间复杂度为 $O(ne)$，稀疏图效率出众，稠密图（不用太密，边数只需要到 $10^6$ 左右）直接 $GG

8.SPFA（已死，还会被卡）——明明只是优化，却有了新名字

其实吧，这个算法就是给 $Bellmam-Ford$ 加了一个队列优化。。。 ~~世界难题：为什么 Dijkstra 优化了还叫 Dijkstra，Bellman-Ford 优化了叫 SPFA~~ 咳咳，言归正传，这个算法就是基于 $Bellman-Ford$ 的思路加上了队列，用邻接表存储 简单来说，就是先把距离数组 $dis$ 初始化成 $∞$（原点为 $s$），然后 $dis[s]=0$；开一个队列，把起点加入队列，并标记入队 然后每次都取出队首，把标记擦掉，然后遍历邻接表进行松弛，更新最短距离，**如果松弛成功，而且被松弛的点不在队列中（未标记）**，就把它加入队尾并标记，直到队列空了，最短路结束 但是既然 $SPFA$ 是 $Bellman-Ford$ 的优化，那么它就还有一项任务没有完成：判断负环 目前主流方法有两种：递归和非递归 先来介绍非递归方式，由于 $Bellman-Ford$ 的特性，我们对一个点最多只需要松弛 $n-1$ 次，如果超过 $n-1$ 次还能松弛就说明有负环。那么我们开一个计数器数组，统计每个点的入队（也可以是出队）次数，如果有任何一个点超过 $n-1$ 次就说明有负环 代码： ```cpp bool SPFA() { queue<int> q;//队列 memset(dis,127/3,sizeof(dis));//初始化一个很大的数 dis[s]=0;//原点最短路是0 q.push(s);//原点入队 vis[s]=1;//标记入队 while(!q.empty())//队列不空说明没跑完 { int k=q.front();//取出队首 q.pop(); vis[k]=0;//擦去标记 ++cnt[k];//统计次数 if(cnt[k]>=n)//如果超过n-1说明有负环 return 0;//报错 for(vector<edge>::iterator it=v[k].begin();it!=v[k].end();++it)//邻接表遍历相连的边 if(dis[it->node]>dis[k]+it->weight)//如果可以松弛 { dis[it->node]=dis[k]+it->weight;//松弛 if(!vis[it->node])//如果被松弛的点不在队列里 { vis[it->node]=1;//标记入队 q.push(it->node);//入队 } } } return 1;//顺利完成 } ``` 然后我们来介绍递归方式，就是判断一个点是否在一条路径上出现多次，如果是，那么它就是有负环的 $PS$：本方法需要需要手打邻接表 ```cpp bool SPFA(int u) { vis[u]=1; for(int k=f[u];k;k=e[k].next)//遍历后面的整个路径 { int v=e[k].v,w=e[k].w; if(d[u]+w<d[v])//能松弛 { d[v]=d[u]+w; if(!vis[v])//不重复 if(!SPFA(v))//如果后面的路径有重复的 return 0;//有负环 else return 0;//重复了，直接说明有负环 } } vis[u]=0;//回溯 return 1;//没有负环 } ``` 然后我们来分析一下 $SPFA$ 的时间复杂度，最坏情况就是退化成 $Bellman-Ford$，为 $O(ne)$，最好情况当然是 $O(1)

（段凡丁曾经证明 SPFA 的时间复杂度是 O(ke)（k 是小常数），但是他的证明已经被证明是错误的，请大家注意）

最后把这道板子送给大家，可以去检验一下自己的 SPFA

[

### 拓展 $1$：$SPFA$ 为何会死/手把手教你出数据卡掉别人的 $SPFA

不知道读者中有没有被 NOI\ 2018\ D1\ T1 坑了的大佬。。。

不是我，我 2018 年还在打普及

当时出题人讲题公然宣称 SPFA 已死，不好，没有管杀还管埋

那么 SPFA 为什么会死呢？

原因就在于它的复杂度不稳定，可以最坏被卡成 O(ne)，然后随便拿出一个较强的数据就轻松 GG。。。

所以只要出题人有心卡你，你是一定会死的

那么读到这里，你是不是也想出一组数据卡掉别人的 SPFA 呢（坏笑

今天我就给大家几种方法出数据

普通 SPFA 的话我们考虑到网格图只要数据可以诱导SPFA进入次短路径就可以大大增加它的时间耗费，所以我们可以用一个有大量次短路径的图，比如网格图和菊♂花♂图♂来卡掉 SPFA，多数 SPFA（包括某些玄学写法）都只能跑过两种图的一种，所以我们可以出一个网格套菊花的图，轻松卡掉一大批 SPFA

然后对于 LLL、mcfx 优化、SLF、SLF 带容错、SLF-swap 等一系列神仙优化（具体看这里），我们也可以出神仙数据把它们卡掉

通常来讲，就是用网格套链式菊花图外挂诱导次短路节点就可以用一个数据卡掉所有的 SPFA

或许有人会说可以用 priority\_queue 优化 SPFA，这样看起来一劳永逸，可以跑神仙数据，但是这却让 SPFA 失去了处理负边权的优势，我们只要出带负边权（或是负环）的数据，就可以卡掉

综上所述，SPFA 要尽量少用

有点意思 不知为何，和去年 $T1$ 相同，居然又考最短路 ~~出题人不动脑子吗，报警了~(b･ω･)~~ 但是出人意料，这次的数据居然**没有卡 $SPFA$** 所以 $SPFA$ ~~诈尸了~~（大雾 好的是活了 其实挺有戏剧性的，也挺好，说不定隔年卡 $SPFA$ 将来就成了 $NOI$ 的传统呢（笑 ~~啪，NOI 2020 没有最短路~~ 但是这只能说明今年出题人比较善（du）良（liu），~~或许去年由于过于毒瘤的数据那个出题人被开除了~~，但是这并不代表我们可以肆无忌惮的使用 $SPFA$，毕竟卡你的方法是有了，卡不卡你是出题人的事，还是别去出题人那里给自己找 $trouble$，最后后悔也来不及 ### 拓展 $2$：用 $SPFA$ 求最长路问题 这个的话，还是比较好想的呢 我们如果把$SPFA$的比较反过来，判断最长路进行松弛，如果出题人发点神经可能会让你过，正常的出题人都会出数据卡你，然后 原 地 打 转 $T$ 到 飞 起 但是考虑到 $SPFA$ 处理负边权的特性，我们可以把边权取相反数，然后跑 $SPFA$，最后再取相反数输出就是最长路了 ## $9.$ 次短路——~~最短路的哥哥~~ 次短路，顾名思义就是除最短路外的最短路（也就是第二短的路），我们现在来讨论如何求它 ~~[可以康康这个](https://www.luogu.com.cn/blog/FrozaFerrari/solution-p1491)（记得点赞~~ 我们设有图 $G(V,E)$，$e(u,v)$ 是其中的一条边的，$w(u,v)$ 是其权值，从 $i$ 到 $j$ 的最短路为 $dis[i][j]$，那么从 $1$ 到 $n$ 的次短路可以表示为： $$\sum_{e(u,v)\in G(v,e)}min(dis[1][u]+w(u,v)+dis[v][n])$$ 所以我们可以先以 $s$ 和 $t$ 分别跑一次最短路（无向图随便跑，有向图需要反向连边然后再跑以 $n$ 为原点的最短路），然后依次枚举每一条 $e(x,y)$，如果结果比最短路长，更新次短路（取最小值），最后找出比最短路长的最短的路径，即次短路 次短路打法很多，单源最短路算法基本都能跑，这里给出 $Dijkstra$ 和 $SPFA$ 代码： $Dijkstra$（无向图）： ```cpp #include<iostream> #include<vector> #include<queue> #include<cstring> using namespace std; struct edge { int node,weight; edge(int node_,int weight_): node(node_),weight(weight_){} }; struct element { int node,value; element(int node_,int value_): node(node_),value(value_){} bool operator <(const element &other) const { return value>other.value; } }; vector<edge> v[1001]; struct qwq { int x,y,w; }e[1001]; int n,m,dis1[1001],dis2[1001],ans,minn,s,t; bool vis[1001]; inline void dijkstra(int start,int dis[]/*传入不同的距离数组*/)//板子 { memset(vis,0,sizeof(vis)); priority_queue<element> q; q.push(element(start,0)); while(!q.empty()) { element k=q.top(); q.pop(); if(vis[k.node]) continue; vis[k.node]=1; dis[k.node]=k.value; for(vector<edge>::iterator it=v[k.node].begin();it!=v[k.node].end();++it) q.push(element(it->node,it->weight+k.value)); } } int main() { cin>>n>>m>>s>>t; for(int i=1;i<=m;++i) { cin>>e[i].x>>e[i].y>>e[i].w; v[e[i].x].push_back(edge(e[i].y,e[i].w)); v[e[i].y].push_back(edge(e[i].x,e[i].w)); } dijkstra(s,dis1);//跑起点最短路 dijkstra(t,dis2);//跑终点最短路 ans=1<<30;//初始化答案 minn=dis1[t];//最短路 for(int i=1;i<=m;++i)//枚举每条边 { if(dis1[e[i].x]+e[i].w+dis2[e[i].y]>minn)//按照公式枚举 { //cout<<dis1[e[i].x]<<" "<<e[i].x<<" "<<e[i].y<<" "<<e[i].w<<" "<<dis2[e[i].y]<<endl;//调试 ans=min(dis1[e[i].x]+e[i].w+dis2[e[i].y],ans);//更新 //cout<<ans<<endl;//调试 } if(dis1[e[i].y]+e[i].w+dis2[e[i].x]>minn) ans=min(dis1[e[i].y]+e[i].w+dis2[e[i].x],ans); } cout<<ans<<endl;//输出 return 0; } ``` $SPFA$（无向图）： ```cpp #include<iostream> #include<vector> #include<queue> #include<cstring> using namespace std; struct edge { int node,weight; edge(int node_,int weight_): node(node_),weight(weight_){} }; int n,m,s,t,dis1[1001],dis2[1001],ans,minn,cnt[1001]; struct qwq { int x,y,w; }e[1001]; bool vis[1001]; vector<edge> v[1001]; inline bool SPFA(int start,int dis[]) { memset(cnt,0,sizeof(cnt)); memset(vis,0,sizeof(vis)); queue<int> q; q.push(start); vis[start]=1; dis[start]=0; while(!q.empty()) { int k=q.front(); q.pop(); vis[k]=0; ++cnt[k]; if(cnt[k]>=n) return 0; for(vector<edge>::iterator it=v[k].begin();it!=v[k].end();++it) if(dis[it->node]>it->weight+dis[k]) { dis[it->node]=it->weight+dis[k]; if(!vis[it->node]) { q.push(it->node); vis[it->node]=1; } } } return 1; } int main() { cin>>n>>m>>s>>t; memset(dis1,127/3,sizeof(dis1)); memset(dis2,127/3,sizeof(dis2)); for(int i=1;i<=m;++i) { cin>>e[i].x>>e[i].y>>e[i].w; v[e[i].x].push_back(edge(e[i].y,e[i].w)); v[e[i].y].push_back(edge(e[i].x,e[i].w)); } if(!SPFA(s,dis1)||!SPFA(t,dis2)) { cout<<"no\n"; return 0; } ans=1<<30;//初始化答案 minn=dis1[t];//最短路 for(int i=1;i<=m;++i)//枚举每条边 if(dis1[e[i].x]+e[i].w+dis2[e[i].y]>minn)//按照公式枚举 { //cout<<dis1[e[i].x]<<" "<<e[i].x<<" "<<e[i].y<<" "<<e[i].w<<" "<<dis2[e[i].y]<<endl;//调试 ans=min(dis1[e[i].x]+e[i].w+dis2[e[i].y],ans);//更新 //cout<<ans<<endl;//调试 if(dis1[e[i].y]+e[i].w+dis2[e[i].x]>minn) ans=min(dis1[e[i].y]+e[i].w+dis2[e[i].x],ans); } cout<<ans<<endl;//输出 return 0; } ``` ## $10.A*$——用心爆搜 ~~广大读者就是有力量，逼我在 3 天内学会了 3 种新算法~~ 好了我就现学现卖，给大家讲解一下 $A*$ 算法（我们之所以讲它，是因为它接下来的 $k$ 短路的**骗分**方法，毕竟可持久化左偏树真的太难写了~~嘤嘤嘤~~） $A*$ 算法（$A\_star$），又名启发式搜索 大家请看这题：[$P2324 [SCOI2005]$骑士精神](https://www.luogu.org/problemnew/show/P2324) 欸 $n=5$ 是不是很小呀（滑稽 而且超过 $15$ 不就不用再走是不是很小呀（滑稽 那是不是可以爆搜呀（危 ~~TLE~~ ~~正解 983ms，你还想爆搜~~ 显然，无论是 $dfs$ 还是 $bfs$（这两个算法统称盲目式搜索），这题妥妥的超时 所以我们需要一个新的算法进行优化 所以我们有了启发式搜索 所谓启发，就是说它在选取路径时不是无脑搜索，而是会考虑代价，然后有目的的进行搜索 比如说你要绕过墙壁去一个位置，$dfs$ 和 $bfs$ 会一直往前走，知道碰壁才转弯，而 $A*$ 会提前预判 $A*$ 的核心思想是一个公式： $$f(n)=g(n)+h(n) $$ $f(n)$ 是代价估值，$g(n)$ 是预计估值，$h(n)$ 是实际耗费 例如骑士精神这一题，如果你己经动了 $s$ 步，还有 $5$ 个骑士未归位，那么如果 $s+5>15$ 就可以直接剪枝，因为到了也不对答案产生任何贡献 显然 $g(n)$ 的好坏直接关乎算法的好坏，一般来讲，$g(n)$ 比最优解大，那么它就是错误的，没有任何意义；$g(n)$ 与最优解相同，此时是理想状态；如果$g(n)$ 比最优解小，那么相差越大性能越差 我以我们要尽可能的让 $g(n)$ 接近最优解，并严格不能超过最优解 对于此题数据规模较小的情况，我们的估价可以粗略一些，不会超时就好 代码： ```cpp #include<iostream> #include<cstdio> using namespace std; const int d[6][6]={{0,0,0,0,0,0}, {0,1,1,1,1,1}, {0,0,1,1,1,1}, {0,0,0,2,1,1}, {0,0,0,0,0,1}, {0,0,0,0,0,0}};//目标状态 const int dx[]={1,1,2,2,-1,-1,-2,-2};//位移 const int dy[]={2,-2,1,-1,2,-2,1,-1}; int t,a[6][6],xa,ya; bool flag; inline int tj()//粗略统计g(n) { int cnt=0; for(int i=1;i<=5;++i) for(int j=1;j<=5;++j) if(d[i][j]!=a[i][j]) ++cnt; return cnt; } void A_star(int x,int y,int f,int s) { int g=tj(); if(!g)//完成了 { flag=1;//标记 return; } if(s+g>f+1)//剪枝，启发式搜索 return; for(int i=0;i<8;++i)//跳一步 { int xx=x+dx[i],yy=y+dy[i]; if(xx<=0||xx>5||yy<=0||yy>5)//判断越界 continue; swap(a[xx][yy],a[x][y]);//跳 A_star(xx,yy,f,s+1);//继续搜 swap(a[xx][yy],a[x][y]);//回溯 } } int main() { scanf("%d",&t); while(t--) { for(int i=1;i<=5;++i) for(int j=1;j<=5;++j) { char c; cin>>c; if(c=='*')//处理成数字 { xa=i,ya=j; a[i][j]=2; } else a[i][j]=c-'0'; } for(int i=1;i<=15;++i) { flag=0; A_star(xa,ya,i,0); if(flag) { printf("%d\n",i); break; } } if(!flag) puts("-1"); } return 0; } ``` ## $11.k$ 短路——最短路家族的毒瘤算法 定义：有向带权图中，从起点到终点（可以重复经过同一个点）的不严格递增的第 $k$ 短路径长度 来看道题[P2483 【模板】k短路（[SDOI2010]魔法猪学院）](https://www.luogu.org/problemnew/show/P2483) 标准的 $k$ 短路了 当然可以爆搜到第 $k$ 短的，也一定会超时 还有一种神仙算法是连续跑 $k-1$ 次次短路。。。挺好写的但是也会 $T$ 飞 我们可以尝试把$Dijkstra$或$SPFA$和$A*$结合起来（优先使用$Dijkstra$） 对于 $A*$ 思路的分析，依然使用公式： $$f(x)=g(x)+h(x)$$ $f(x)$ 是~~咕值~~估值，$g(x)$ 是预算，我们可以采用 $dis[x][end]$ 的值（从 $x$ 到 $end$ 的最短路，我们可以用 $Dijkstra+$ 反向建图先跑出来），$h(n)$ 采用 $start$ 到 $x$ 的路径总长度 优先访问 $f(x)$ 更小的点，因为它更有可能成为最短路，然后是次短路、第三短路…… 这样我们不断搜索，到第 $k$ 次到达 $end$ 时直接结束输出答案即可 代码（别急着抄，只有 $76pts$）： ```cpp #include<iostream> #include<cstdio> #include<vector> #include<queue> #include<cstring> using namespace std; int n,m,ans; double kkk; struct edge { int node; double weight; edge(int node_,double weight_): node(node_),weight(weight_){} }; struct element { int node; double value; element(int node_,int value_): node(node_),value(value_){} bool operator <(const element &other) const { return value>other.value; } }; struct AC { int node; double h,f; AC(int node_,double h_,double f_): node(node_),h(h_),f(f_){} bool operator <(const AC &other) const { return f>other.f; } }; vector<edge> v[5001],vv[5001]; double dis[5001]; int cnt[5001]; bool vis[5001]; inline int read() { int x=0; char c=getchar(); while(c<'0'||c>'9') c=getchar(); while(c>='0'&&c<='9') { x=(x<<1)+(x<<3)+c-'0'; c=getchar(); } return x; } inline void dijkstra() { priority_queue<element> q; q.push(element(n,0.0000)); memset(dis,127/3,sizeof(dis)); while(!q.empty()) { element k=q.top(); q.pop(); if(vis[k.node]) continue; vis[k.node]=1; dis[k.node]=k.value; for(vector<edge>::iterator it=vv[k.node].begin();it!=vv[k.node].end();++it) q.push(element(it->node,it->weight+k.value)); } } inline void A_star(int kk) { priority_queue<AC> q;//用优先队列自动按f(x)排序，实现A*思想 q.push(AC(1,0.000,0.000)); while(!q.empty()) { AC k=q.top(); q.pop(); if(k.f>kkk) return; ++cnt[k.node]; if(k.node==n)//找到一条 { kkk-=k.f; ++ans; continue; } if(cnt[k.node]>kk)//超过预算过掉 continue; for(vector<edge>::iterator it=v[k.node].begin();it!=v[k.node].end();++it)//遍历 q.push(AC(it->node,it->weight+k.h,it->weight+k.h+dis[it->node])); } } int main() { n=read(),m=read(); scanf("%lf\n",&kkk); for(int i=1;i<=m;++i) { int x,y; double w; x=read(),y=read(); scanf("%lf",&w); v[x].push_back(edge(y,w)); vv[y].push_back(edge(x,w)); } dijkstra(); A_star(kkk/dis[1]); printf("%d\n",ans); return 0; } ``` 然后我们发现这代码被某个神仙的数据卡掉了。。。（$bzoj$ 能过，但是洛咕不行） ~~出毒瘤数据的神仙，我们一起揍他~~ 这是由于如果数据是一个 $n$ 元环，那么 $A*$ 的时间复杂度为 $O(nk)$，而且 $A*$ 的空间复杂度巨大，是指数级的所以用 $A*$ 会 $MLE+TLE$。。。 那么如果数据是一堆 $n$ 元环呢（就是本题数据点 $\#11$，也就是网格图，里面好像还有菊花，顺手把 $SPFA$ 也卡掉了）。。。 ### 我们需要用**可持久化左偏树**解决本题 ~~但是你们逼我速成 3 个算法也就算了，第 4 个我真的吃不消，啊啊啊左偏树太难辣~~ 在这里给出[题解链接](https://blog.bill.moe/SDOI2010-magic/)，大家可以先自己学习，**我也尽快学习，学会了会赶紧来 $update$ 的 $QAQ$** ~~我保证不咕咕~~（$flag

好吧看来正解是学不会了（咕咕咕咕咕咕咕咕咕咕咕咕咕咕）。。。照着代码自己打了一遍都有 21 处编译错误，我还不会改。。。太菜了那我就给大家直接口胡讲一讲吧。。。

我们用 Dijkstra 在反向建的图里跑，然后我们根据这个最短路建出一个最短路树来，然后乱搞给这个树加边，每加一条非树边，就会使路径长度加长 \delta=dis[u]+e(u,v)-dis[v]

那么路径 p 的总长为 dis_{min}+\sum\limits_{e∈p,e∈G-T}\delta(e)

我们可以用可并堆，先根据图建造一颗最短路树，然后不断加边，用数据结构维护，直到加到猪猪能量【雾】不够的时候跳出（这里我也不是太清楚，大体是这个样子吧。。。）

那我就先讲这么多吧

12. 关于源点、汇点和边权——技巧性卡常

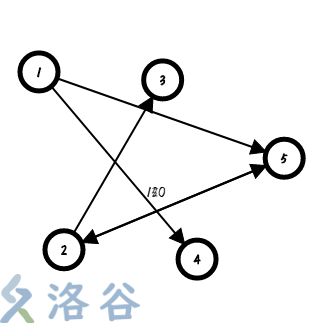
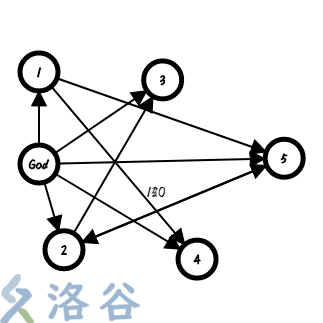
比如说[$P2648$ 赚钱](https://www.luogu.org/problem/P2648) 题目里有这么一句话：  也就是说没有一个固定的起点和终点，跑 $n$ 次 $SPFA$ 怕是要 $T$ 到 飞 起 ~~假的，这题数据水，直接跑 n 次最短路也能水过去~~ ### ~~淦。~~ 那该怎么办办呢？ 其实，比如我们画出一个图（就是样例，但是两个边权重合了，大家凑合着看 qwq）：  然后我们可以用一个上帝视角，建出一个超级源点~~上帝点~~，然后给他和每个点连一条权值是 $0$ 的边  然后这个问题就被我们转化成了一个单源最短路问题 输出时可以枚举每个变量，也可以再开一个超级汇点，连权值是 $0$ 的边，直接输出 还有一个问题就是点权转边权 这里每个点是有权值的，我们需要把它们放进边里，不难想到，直接在每条边权值里直接加上一个 $d$ 就行了，因为新到一个城市一定可以得到 $d$ 元 在运用上面讲过的最长路写法+负环判断，就可以轻松过掉啦 [代码](https://www.luogu.org/blog/85682/solution-p2648) 进去记得点赞（大雾 ## $13.$分层图——~~飞机~~ 大家看这道题：[$[JLOI2011]$飞行路线](https://www.luogu.org/problem/P4568) 最短路，显而易见 但是这个免费 $k$ 次却是相当恶心人，导致我们不能算出最短路然后再贪心去掉前 $k$ 大的边，因为这不能保证无后效性 我们考虑一种图，叫做分层图，在本题中，我们可以把图分成 $k+1$ 层（重边的边权又重合了，不好意思）：  ~~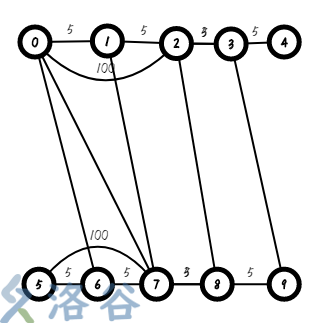山寨二分图（大雾~~ 实际上，我们就是把一个图复制成 $k$ 层，然后没输入一条边，就增加双向边 $\sum_{i=1}^k(n*(i-1)+u\underrightarrow{\text{\ \ \ \ \ \ 0\ \ \ \ \ \ }}n*i+j)$ 代表做了一次免费飞机（大雾  然后最后从 $s\rightarrow t+(n*k)$ 的最短路就是答案 ```cpp #include<iostream> #include<cstdio> #include<vector> #include<queue> using namespace std; struct edge { int node,weight; edge(int node_,int weight_): node(node_),weight(weight_){} }; vector<edge> v[1000001]; struct element { int node,value; element(int node_,int value_): node(node_),value(value_){} bool operator <(const element &other) const { return value>other.value; } }; int s,t,n,m,h,dis[1000001],ans; bool vis[1000001]; inline void dijkstra() { priority_queue<element> q; q.push(element(s,0)); while(!q.empty()) { element k=q.top(); q.pop(); if(vis[k.node]) continue; vis[k.node]=1; dis[k.node]=k.value; for(vector<edge>::iterator it=v[k.node].begin();it!=v[k.node].end();++it) if(!vis[it->node]) q.push(element(it->node,it->weight+k.value)); } } int main() { scanf("%d%d%d",&n,&m,&h); scanf("%d%d",&s,&t); for(int i=1;i<=m;++i) { int x,y,w; scanf("%d%d%d",&x,&y,&w); v[x].push_back(edge(y,w)); v[y].push_back(edge(x,w)); for(int j=1;j<=h;++j) { v[x+(j-1)*n].push_back(edge(y+j*n,0)); v[y+(j-1)*n].push_back(edge(x+j*n,0)); v[x+j*n].push_back(edge(y+j*n,w)); v[y+j*n].push_back(edge(x+j*n,w)); } } dijkstra(); printf("%d\n",(m<h? 0:dis[t+n*h]));//有个毒瘤数据，需要特判 return 0; } ``` ## $14.$ 结语——终于还是再见 最后送大家两句金玉良言： ### 正边权（数据相对较大）不要用 $SPFA$ 和 $Bellman-Ford$，用了就是作死 ### 学好堆优化 $Dijkstra$，关键时刻很有用哒~ #### ヾ(￣▽￣)$Bye$~$Bye$~