题解 P2448 【无尽的生命】
IC_QQQ
2019-05-13 10:21:07
### 求逆序对
但这肯定不是普通的求逆序对题目:数据范围太大了,会超时。
尽管数据范围很大,但是**k**不大,最多只牵涉到了**2k**个数。
我们举个例子:
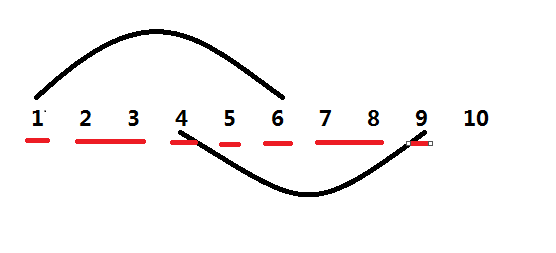
需要交换的两组数是:1—6 , 4—9。
我们可以发现,数2、3可以看做一个**整体**,数7、8可以看做一个**整体**。
也就是说,一段**连续**的数,我们可以把它看做一个**整体**,记录下它的代表元**id**和权值**t**。
什么意思呢?我们来看处理之后应该是怎样的:
(1,1) , (2,2) , (4,1) , (5,1) , (6,1) , (7,2) , (9,1)
我们就把所有的连续区间记做了**二元组**。用这个区间最小的数作**代表元**,**权值**就是区间数的个数。
然后进行交换:
(6,1),(2,2),(9,1),(5,1),(1,1),(7,2),(4,1)
剩下的就是普通的求逆序对了。
别忘了离散化。
### 代码:
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5;
int n,st,tot;
struct aaa{
int x,y;
}Q[N];//记录需要交换的数
int t[2*N],id[2*N];//t:权值。id:代表元
int s[2*N],row[22*N];
ll ans,c[2*N];
int query(int val){//离散化的查询
return lower_bound(row+1,row+1+tot,val)-row;
}
void adds(int pos,ll w){//
for(;pos<=tot;pos+=pos&-pos) c[pos]+=w;
return;
}
ll asks(int pos){
ll sum=0;
for(;pos;pos-=pos&-pos) sum+=c[pos];
return sum;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d",&Q[i].x,&Q[i].y);
s[i]=Q[i].x;s[i+n]=Q[i].y;
}
sort(s+1,s+1+2*n);
st=unique(s+1,s+1+2*n)-(s+1);
row[++tot]=s[1];t[tot]=1;
for(int i=2;i<=st;i++){
if(s[i]-s[i-1]>1){
row[++tot]=s[i-1]+1;
t[tot]=s[i]-s[i-1]-1;
}
row[++tot]=s[i];t[tot]=1;
}
for(int i=1;i<=tot;i++) id[i]=i;
for(int i=1;i<=n;i++){
int x=query(Q[i].x),y=query(Q[i].y);
swap(t[x],t[y]);
swap(id[x],id[y]);
}
for(int i=tot;i>=1;i--){
ans+=asks(id[i]-1)*(ll)t[i];//注意,乘法
adds(id[i],(ll)t[i]);
}
printf("%lld",ans);
return 0;
}
```