题解 P4013 【数字梯形问题】
Iowa_BattleShip
2018-04-03 20:15:16
很明显,这题是道**最大费用最大流**,只不过强行加上规则来导致你的码量轻松上天。
下面将三个规则一个一个解释如何建图
#### 规则一
~~其实我认为三个规则里第一个反而是相对最难的~~
$m$条路径皆不能相交,即点和边都不能相交。
首先,要使得路径上的点不相交(重合),即每个点只能走一次,因此我们想到将每个点拆成两个点$X<i,j>$和$Y<i,j>$,并在$X<i,j>$和$Y<i,j>$之间连一条容量为$1$,费用为该点本身的数值的边,当选中这条边就表示某条路径经过点$<i,j>$,并将该点数值计入。
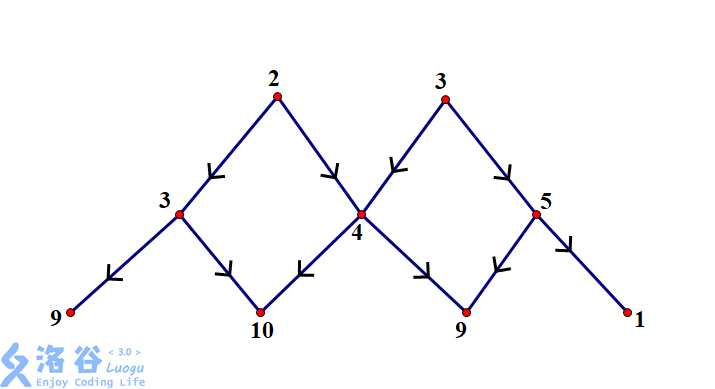
接下来是连边,其实很简单,将点$Y<i,j>$向$X<i+1,j>$和$X<i+1,j+1>$连上一条边,而根据下图,显然我们可以看出当点不相交时,边肯定是不会相交的,所以我们在添加边的时候容量是可以随便开的(当然要$≥1$),费用则赋为$0$。
最后按照惯例,给图加上一个超级源点$S$和超级汇点$T$,$S$向每个$X<1,i>$连一条容量为$1$,费用为$0$的边;每个$<n,i>$向$T$连一条容量为$1$,费用为$0$的边。
然后跑一波最大费用最大流即可。
#### 规则二
这下只要求边不相交(重合)了,所以可以不用拆点了。
直接连边,给每个点$<i,j>$向$<i+1,j>$和$<i+1,j+1>$连上一条边,容量为$1$(因为每条边只能走一次,而根据上图,边只会重合),费用则赋为点$<i,j>$所表示的数值,即经过这条边表示选取了这个点的数(其实规则一中也可以这样连边,然后将拆点间的边的容量改为$0$即可)。
最后依旧定个超级源点$S$和超级汇点$T$,$S$依旧向每个$<1,i>$连一条容量为$1$,费用为$0$的边;而每个$<n,i>$向$T$连一条容量为$inf$的边(因为每个$<n,i>$都可以取$inf$次),费用为$<n,i>$所表示的数值。
然后依旧一波最大费用最大流。
#### 规则三
~~其实就是没有规则~~
只需将规则二所连的边,除了与$S$连的边,其他边的容量全部改为$inf$就好,因为所有点和边都可以重复走了。
然后一波最大费用最大流带走$AC$~
$PS:$关于规则三我认为完全可以用$DP$跑过去,将这个梯形拆成$m$个三角形,然后直接$DP$,复杂度大概为$O(\frac{1}{2}n^2m)$,是可以跑过去的。
最后上~~冗长的~~代码
```cpp
#include<cstdio>//我用的是带SPFA的EK
#include<cstring>
using namespace std;
const int N=1e5+10;
int fi[N],di[N<<1],da[N<<1],ne[N<<1],co[N<<1],q[N],la[N],nm[N],dis[N],a[22][50],b[22][50],l,st=1e5+1,ed=1e5+2,s;
//fi,di,da,ne,co存边,q为队列,la,nm记录在SPFA中搜到的分层图,dis记录费用,a为原图,b为原图中每个数对应的编号,st是源点,ed是汇点
bool v[N];//在SPFA中记录该点有无在队列中
int re()//快读
{
int x=0;
char c=getchar();
bool p=0;
for(;c<'0'||c>'9';c=getchar())
p=(c=='-'||p)?1:0;
for(;c>='0'&&c<='9';c=getchar())
x=x*10+(c-'0');
return p?-x:x;
}
void add(int x,int y,int z,int c)//加边
{
di[++l]=y;
da[l]=z;
co[l]=c;
ne[l]=fi[x];
fi[x]=l;
di[++l]=x;
da[l]=0;
co[l]=-c;
ne[l]=fi[y];
fi[y]=l;
}
inline int minn(int x,int y)//手写min
{
return x<y?x:y;
}
void cl()//每次跑完后重建图前的清空
{
l=s=0;
memset(fi,0,sizeof(fi));
memset(di,0,sizeof(di));
memset(da,0,sizeof(da));
memset(ne,0,sizeof(ne));
memset(co,0,sizeof(co));
}
bool spfa()//SPFA
{
int head=0,tail=1,x,y,i;
memset(dis,-50,sizeof(dis));//初始化为-inf
memset(v,0,sizeof(v));
q[1]=st;
dis[st]=0;
while(head!=tail)
{
head++;
x=q[head];
v[x]=0;
for(i=fi[x];i;i=ne[i])//枚举边
{
y=di[i];
if(da[i]>0&&dis[y]<dis[x]+co[i])//找到最大费用
{
dis[y]=dis[x]+co[i];
la[y]=x;//记录分层图
nm[y]=i;
if(!v[y])//若不在队列则加入队列
{
tail++;
q[tail]=y;
v[y]=1;
}
}
}
}
return dis[ed]>0;//判断ed有无走到
}
void ek()//EK
{
int i,mi;
while(spfa())
{
mi=1e9;
for(i=ed;i!=st;i=la[i])//从分层图的ed枚举到st,找到最小的流量
mi=minn(mi,da[nm[i]]);
s+=mi*dis[ed];//累计每次的费用
for(i=ed;i!=st;i=la[i])//修改容量
{
da[nm[i]]-=mi;
da[((nm[i]+1)^1)-1]+=mi;
}
}
}
int main()
{
int i,j,n,m,k,o,nu=0;
k=m=re();
n=re();
o=(((m*n)<<1)+n*n-n)>>1;//等差数列求和公式+梯形面积公式,算出一共有多少数,拆点时区分编号用
for(i=1;i<=n;i++,k++)
for(j=1;j<=k;j++)
{
a[i][j]=re();
b[i][j]=++nu;//输入的同时给点赋上编号
}
k=m;
for(i=1;i<=k;i++)
add(st,b[1][i],1,0);//连上源点
for(i=1;i<n;i++,k++)
for(j=1;j<=k;j++)
{
add(b[i][j],b[i][j]+o,1,a[i][j]);//给拆点间连边
add(b[i][j]+o,b[i+1][j],1,0);//向左下和右下连边
add(b[i][j]+o,b[i+1][j+1],1,0);
}
for(i=1;i<=k;i++)
{
add(b[n][i],b[n][i]+o,1,a[n][i]);//拆点间连边
add(b[n][i]+o,ed,1,0);//向汇点连边
}
ek();//跑最大费用最大流
printf("%d\n",s);
cl();//清空重建
k=m;
for(i=1;i<=k;i++)
add(st,b[1][i],1,0);//连源点
for(i=1;i<n;i++,k++)
for(j=1;j<=k;j++)
{
add(b[i][j],b[i+1][j],1,a[i][j]);//不需要拆点了,直接向左下右下连边
add(b[i][j],b[i+1][j+1],1,a[i][j]);
}
for(i=1;i<=k;i++)
add(b[n][i],ed,1e9,a[n][i]);//向汇点连边,容量为inf
ek();//再来跑一遍
printf("%d\n",s);
cl();//同样清空
k=m;
for(i=1;i<=k;i++)
add(st,b[1][i],1,0);//连汇点
for(i=1;i<n;i++,k++)
for(j=1;j<=k;j++)
{
add(b[i][j],b[i+1][j],1e9,a[i][j]);//向左下右下连边,容量为inf
add(b[i][j],b[i+1][j+1],1e9,a[i][j]);
}
for(i=1;i<=k;i++)
add(b[n][i],ed,1e9,a[n][i]);//向汇点连边,容量为inf
ek();//最后一波带走~
printf("%d\n",s);
return 0;
}
```