XOR-ranges解析
Lucky_Glass
·
·
题解
# 题面
> Linked 洛谷 CF1456E
日常写洛谷翻译(?)
有 n 个位数不超过 K 的二进制变量 x_1,x_2,\dots,x_n,其中 x_i 的取值范围是 [l_i,r_i]。
给出数列 c_0,c_1,\dots,c_{K-1},并由此定义一个代价函数 f(x):
f(x)=\sum_{i=0}^{K-1}(\lfloor\tfrac x{2^i}\rfloor\bmod 2)\cdot c_i
换句话说,f(x) 表示:如果 x 的二进制第 i 位是 1,则代价加上 c_i。
现在你需要确定每个变量的取值,使得 \sum_{i=2}^nf(x_i\mathbf{\ xor\ }x_{i-1}) 最小;输出该最小值。
## \# 解析
的确是很麻烦的一道题……需要一步步解决。
首先看到 $l_i,r_i$ 的限制,又是一个二进制数,容易联想到数位DP。数位DP有一个关键——**数位限制的解除**,即限制解除后,剩下的数位可以随便乱选。
又因为是二进制下讨论,数位限制解除的方式非常有限:
- 首先 $l_i,r_i$ 的高位可能会有一段相同的数位,在这些数位不可能解除限制;
- 在从高到低第一个 $l_i,r_i$ 不同的数位(一定是 $l_i$ 该位为 $0$,$r_i$ 该位为 $1$),若 $x_i$ 该位选择 $0$,则**解除了上界限制**,否则**解除了下界限制**;
- 若解除了上界限制,继续考虑下界 $l_i$ 的限制,在之后的某一个 $l_i$ 为 $0$ 的数位,如果 $x_i$ 该位选择 $1$,则**解除了所有限制**,接下来**可以贪心地选取代价最小的方案**。(解除了下界限制同理)
当然也有**可能不解除限制**,直接取 $l_i$ 或 $r_i$,比较特殊,之后需要处理。
“解除的方式有限”体现在方式数小于 $2K$——从解除了上/下界限制开始,分别有小于 $K$ 个数位可以解除所有限制。这 $2K$ 个方式分别对应了**解除限制之前的已经固定的** $x_i$ 的 $2K$ 种取值。下面是一个例子(~~有什么解释不清楚的就上图~~):
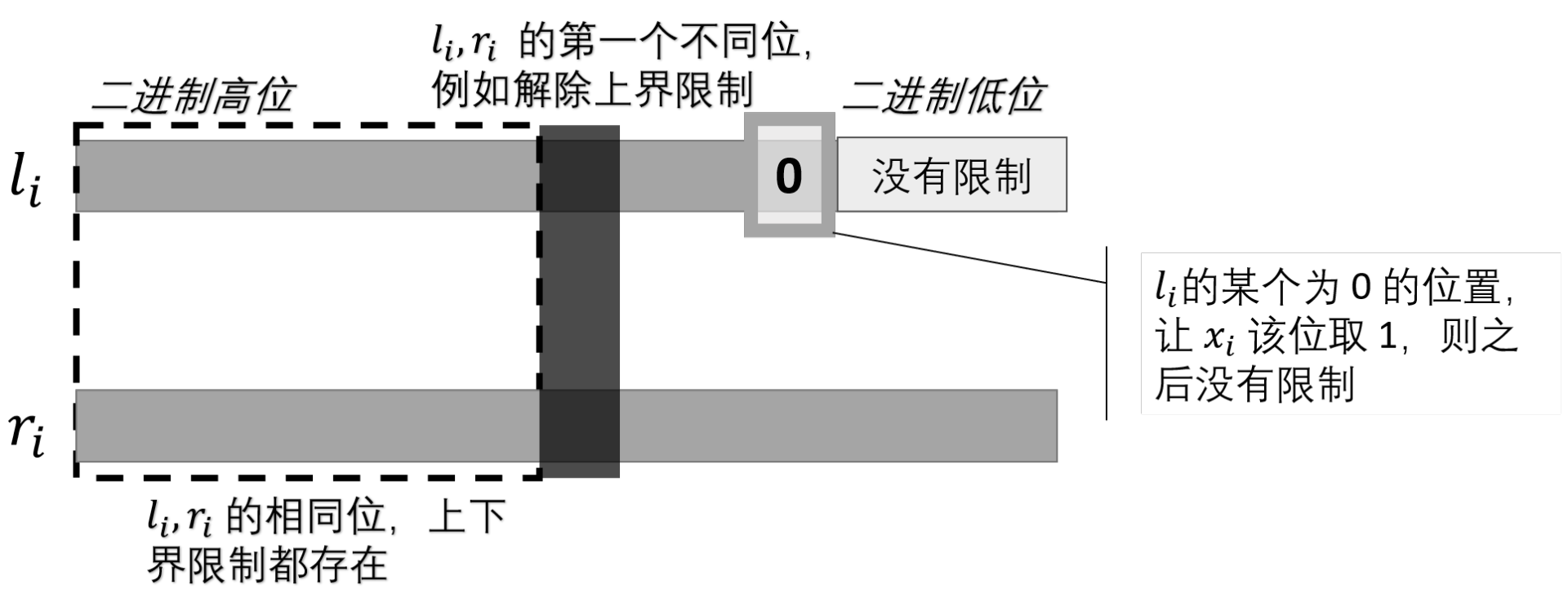
解除所有限制后可以贪心选取,怎么贪心?考虑到不同的变量解除限制的位数有高有低;假如我们*已经确定了每个变量怎么解除限制*,那么每个变量**解除限制前的数位就已经固定了**,就可能碰到下面这种情况($l+1=m=r-1$):
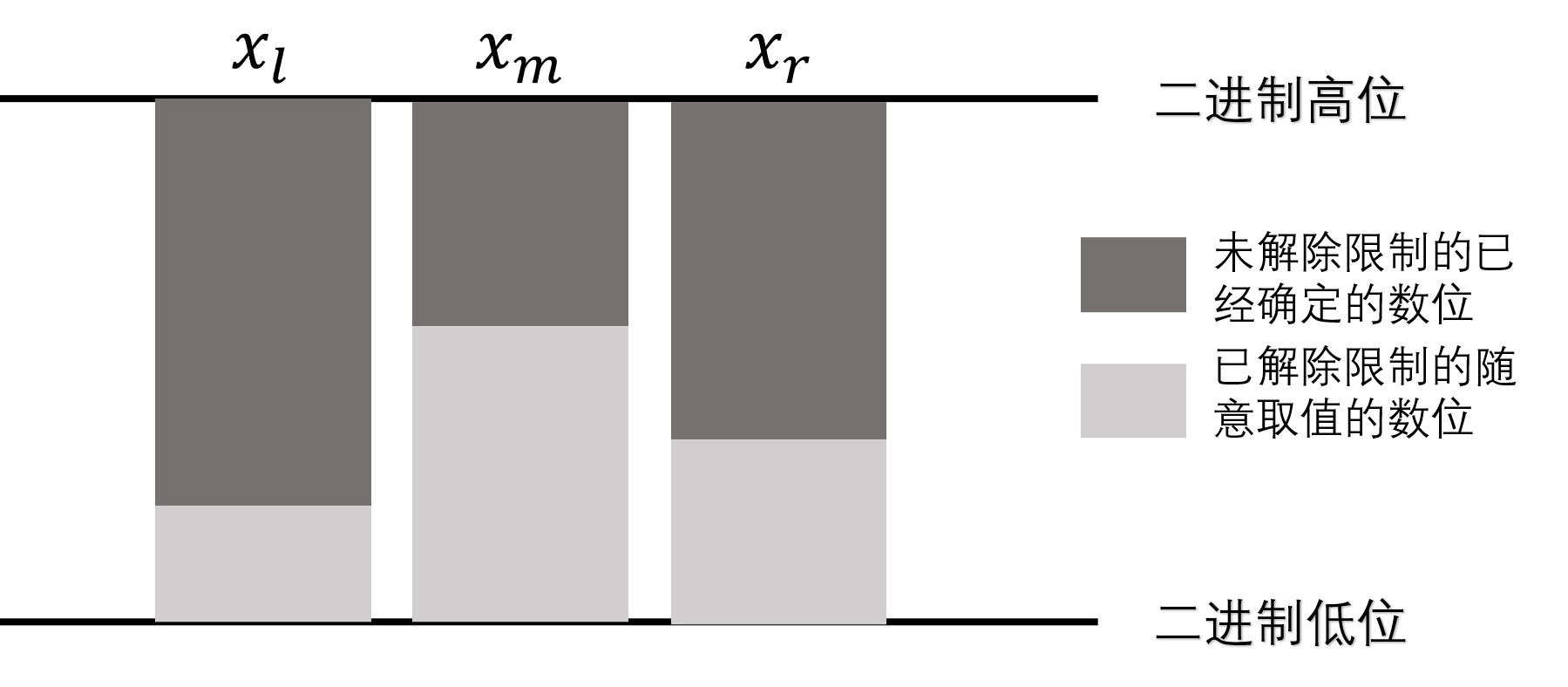
怎么贪心地选取 $x_m$ 的取值使得 $l,m,r$ 三数的代价和最小?已经固定的代价是不可改变的,所以只需要最小化 $x_m$ 随意取值的部分产生的**额外贡献**。
不难发现,让 $x_m$ 可以随意取值的部分和 $x_l$ 一样即可(也可以与 $x_r$ 一样)——这样 $x_l\mathbf{\ xor\ }x_m$ 产生的**额外贡献**为 $0$,而 $x_m\mathbf{\ xor\ }x_r$ 的额外代价恰好为 $x_l\mathbf{\ xor\ }x_r$。我们发现可以直接忽略 $x_m$。
上面考虑了连续三个数的代价。实际上,任意 $x_l,x_r$ 之间,如果已经固定的位数少于 $x_l,x_r$,就可以忽略掉中间的数的额外代价。
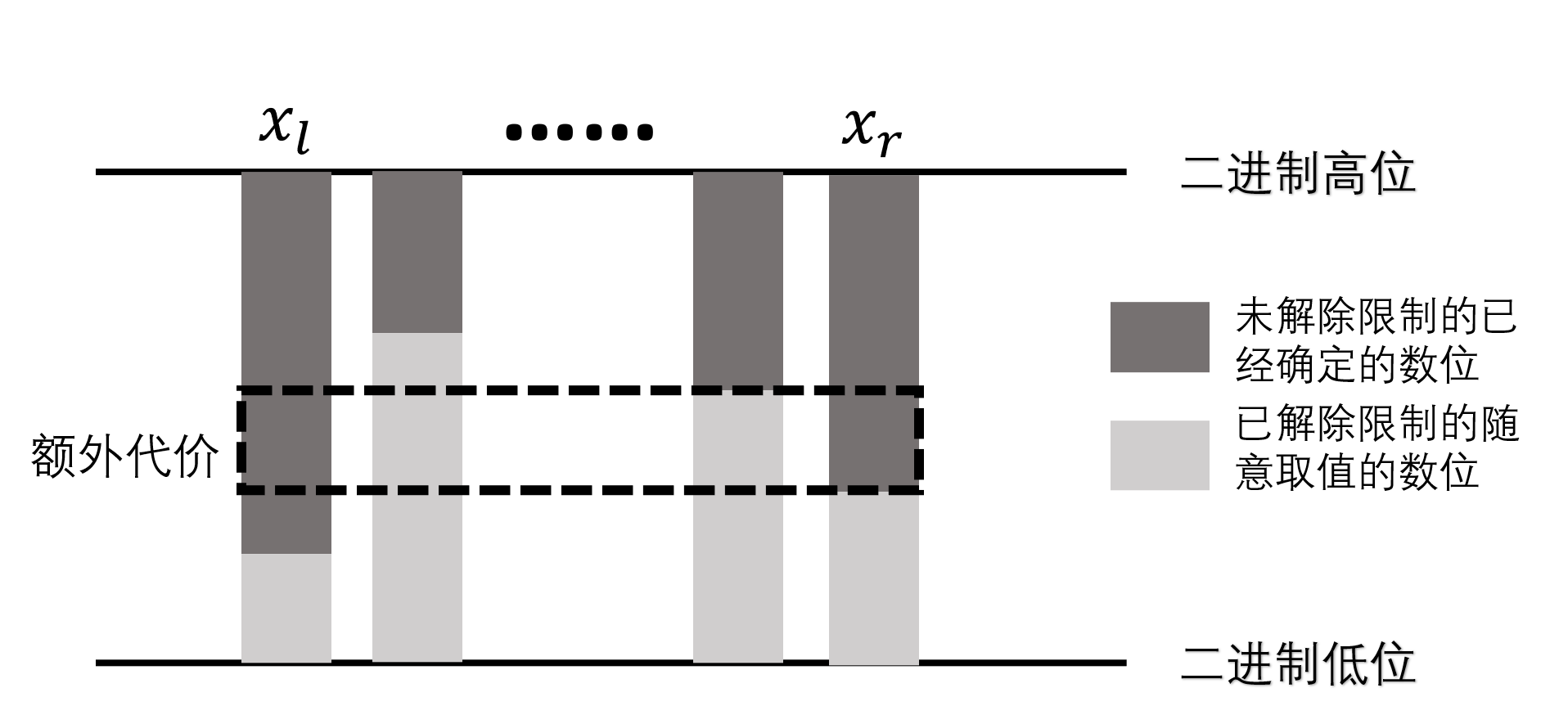
只有两侧的**位数固定得较多**的数才计算代价?这让我们想起了什么?笛卡尔树?——区间DP。
定义 DP 状态 $f(l,r,p,q,h)$ 表示 $[l,r]$ 区间内的所有数已经固定的位数都不超过 $h$,而且 $l-1,r+1$ 的固定位数高于 $h$(这意味着区间两侧的数在 $h$ 以上的数位都已经确定了),$p,q$ 是 01 标记,分别表示 $l-1,r+1$ 是先释放的上边界(0)还是先释放的下边界(1)。
如果先释放的上边界,则 $x_i$ 的 $h$ 以上的位数就与 $l_i$ 相同(除了释放所有边界的数位,该位与 $l_i$ 相反)。
如何转移?由于是 “$\le h$”,就可以分成 “$< h$” 和 “$=h$”。小于 $h$ 的转移如下:
$$
\begin{aligned}
f(l,r,p,q,h)=f(l,r,p,q,h+1)+cost(l-1,r+1,h)
\end{aligned}
$$
由于 $[l,r]$ 内第 $h$ 位都可以随便取,其代价根据上文分析就是区间两侧 $l-1,r+1$ 的第 $h$ 位的代价。
而 $=h$ 的转移如下图:
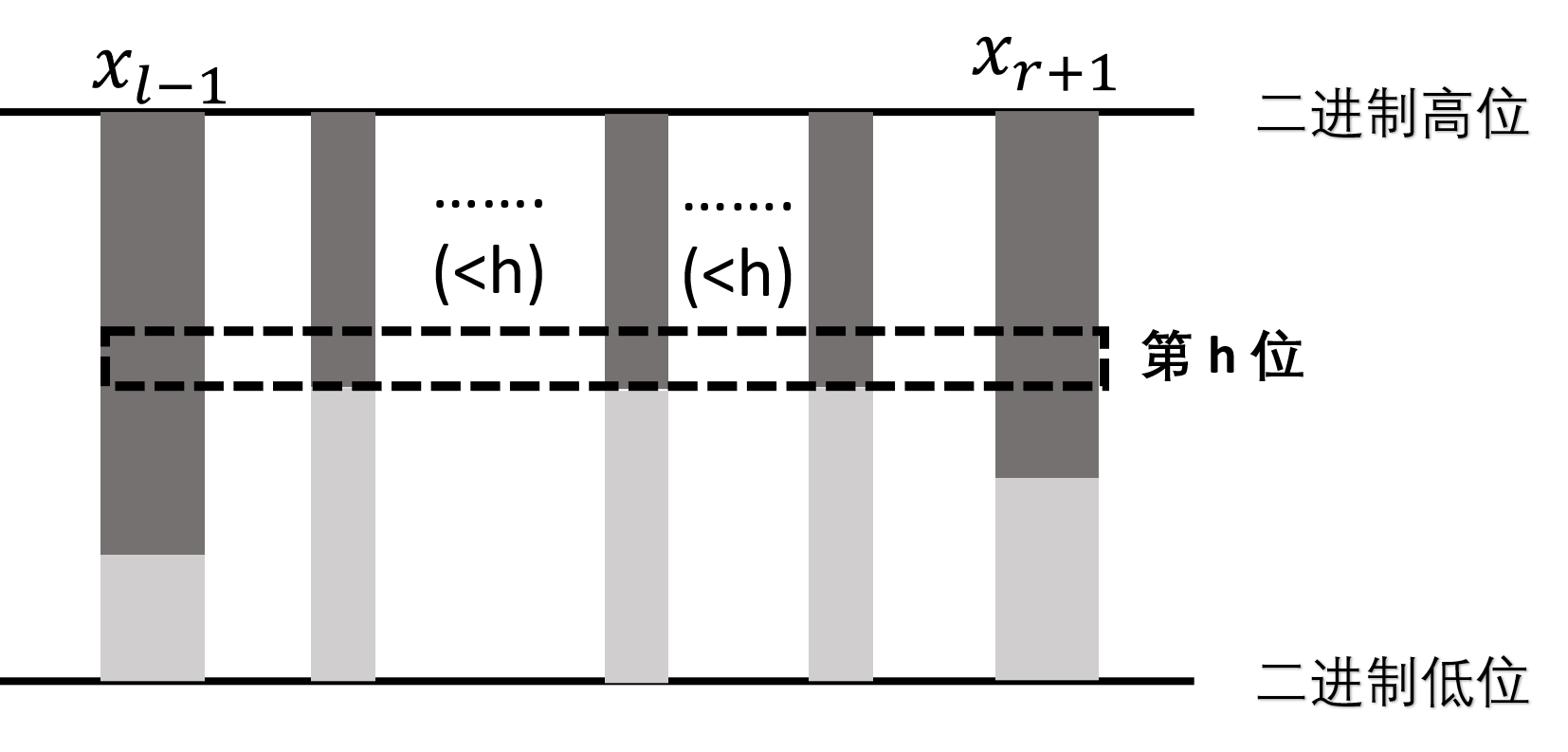
于是可以用一个 $O(n)$ 的 DP 在 $[l,r]$ 内做转移:$g_{i,p}$ 表示已经决策了 $x_{r\sim i}$ 是否在第 $h$ 位释放,且 $x_i$ 在第 $h$ 位释放,$p$ 是 01 标记,表示 $x_i$ 是释放下界还是释放上界(这样就可以确定 $x_i$ 到底长什么样)。
转移比较简单:
$$
\begin{cases}
g_{l-1,p}=0\\
g_{l-1,\lnot p}=+\infty\\
g_{i,k}=\min\limits_{j< i}\{g_{j,w}+F(i+1,j-1,w,k,h-1)+cost(i,j,h)\}\\
F(l,r,p,q,h)=\min\{g_{i,k}+cost(i,r+1,h)\}
\end{cases}
$$
好像这样就做完了?
但是我们只考虑了每个 $x_i$ 都释放了限制的情况,当然可以直接取上下界限制而不释放。所以最外层再套一个 DP,决策哪些数不释放边界:
$$
h_{i,p}=\min\{h_{j,q}+F(j+1,i-1,q,p,0)\}
$$
(转移中的 $x_i,x_j$ 都不释放边界,$h$ 数组的第二位表示决策的是上界还是下界)
---
## \# 源代码
```cpp
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=55;
typedef long long ll;
template<class T>inline T Read(T &r){
int b=1,c=getchar();r=0;
while(c<'0' || '9'<c) b=c=='-'? -1:b,c=getchar();
while('0'<=c && c<='9') r=(r<<1)+(r<<3)+(c^'0'),c=getchar();
return r*=b;
}
#define cmin(a,b) (a=min(a,b))
const ll INF=0x3f3f3f3f3f3f3f3f;
int n,m;
ll cst[N],lim[N][2],f[N][N][2][2][N],g[N][N][N][2],h[N][2];
ll sta[N][N][2];
ll F(int L,int R,int bl,int br,int H){
if(H>=m) return L<=R? INF:0;
if(~f[L][R][bl][br][H]) return f[L][R][bl][br][H];
ll &u=f[L][R][bl][br][H],lasv;
u=INF;
if(L==1 || R==n) cmin(u,F(L,R,bl,br,H+1));
else cmin(u,F(L,R,bl,br,H+1)+((lim[L-1][bl]^lim[R+1][br])>>H&1)*cst[H]);
for(int i=L-1;i<=R;i++) g[L][R][i][0]=g[L][R][i][1]=INF;
g[L][R][L-1][bl]=0;
for(int i=L;i<=R;i++)
for(int p=0;p<2;p++){
if(sta[i][H][p]==-1) continue;
for(int j=L-1;j<i;j++)
for(int q=0;q<2;q++){
if(g[L][R][j][q]==INF) continue;
if(j==L-1){
lasv=j>=1? lim[L-1][bl]:sta[i][H][p];
cmin(g[L][R][i][p],g[L][R][j][q]+F(j+1,i-1,q,p,H+1)+((lasv^sta[i][H][p])>>H&1)*cst[H]);
}
else cmin(g[L][R][i][p],g[L][R][j][q]+F(j+1,i-1,q,p,H+1)+((sta[j][H][q]^sta[i][H][p])>>H&1)*cst[H]);
}
if(R+1<=n) lasv=lim[R+1][br];
else lasv=sta[i][H][p];
cmin(u,g[L][R][i][p]+F(i+1,R,p,br,H+1)+((sta[i][H][p]^lasv)>>H&1)*cst[H]);
}
return u;
}
int main(){
//freopen("input.in","r",stdin);
memset(sta,-1,sizeof sta);
memset(f,-1,sizeof f);
Read(n),Read(m);
for(int i=1;i<=n;i++){
Read(lim[i][0]),Read(lim[i][1]);
if(lim[i][1]-lim[i][0]<=1){
sta[i][0][0]=lim[i][0];
sta[i][0][1]=lim[i][1];
}
else{
for(int j=m-1;j>=0;j--)
if((lim[i][0]^lim[i][1])>>j&1){
for(int k=j-1;k>=0;k--){
if(!(lim[i][0]>>k&1))
sta[i][k][0]=lim[i][0]^(1ll<<k);
if(lim[i][1]>>k&1)
sta[i][k][1]=lim[i][1]^(1ll<<k);
}
break;
}
}
}
for(int i=0;i<m;i++) Read(cst[i]);
for(int i=1;i<=n+1;i++) h[i][0]=h[i][1]=INF;
for(int i=1;i<=n+1;i++){
for(int j=0;j<i;j++){
cmin(h[i][0],h[j][0]+F(j+1,i-1,0,0,0));
cmin(h[i][0],h[j][1]+F(j+1,i-1,1,0,0));
cmin(h[i][1],h[j][0]+F(j+1,i-1,0,1,0));
cmin(h[i][1],h[j][1]+F(j+1,i-1,1,1,0));
}
}
printf("%lld\n",h[n+1][0]);
return 0;
}
```
---
## THE END
### Thanks for reading!